Измерение углов. Транспортир | Математика

Измерить угол — значит найти его величину. Величина угла показывает, сколько раз угол, выбранный за единицу измерения, укладывается в данном углу.

Обычно за единицу измерения углов принимают градус. Градус — это угол, равный    части развёрнутого угла. Для обозначения градусов в тексте, используется знак  °,  который ставится в правом верхнем углу числа, показывающего количество градусов (например, 60°).

Измерение углов транспортиром

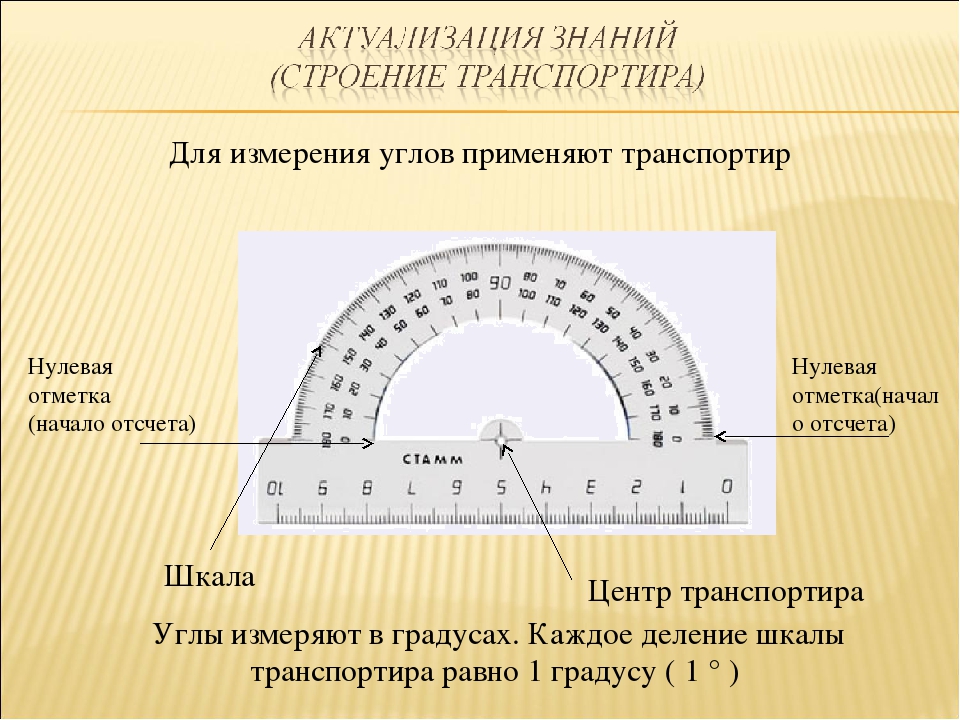
Для измерения углов используют специальный прибор — транспортир:

У транспортира две шкалы — внутренняя и внешняя. Начало отсчёта у внутренней и у внешней шкал располагается с разных сторон. Чтобы получить правильный результат измерения, отсчёт градусов должен начинаться с правильной стороны.

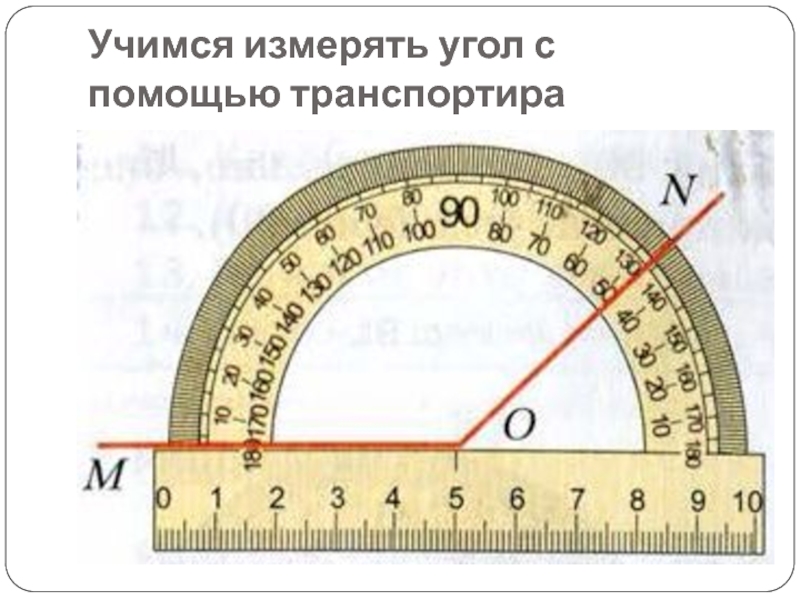
Измерение углов производится следующим образом: транспортир накладывают на угол так, чтобы вершина угла совпала с центром транспортира, а одна из сторон угла прошла через нулевое деление на шкале. Тогда другая сторона угла укажет величину угла в градусах:

Говорят: угол  BOC  равен 60 градусов, угол  MON  равен 120 градусов и пишут:  ∠BOC = 60°,  ∠MON = 120°.

Для более точного измерения углов используют доли градуса: минуты и секунды. Минута — это угол, равный    части градуса. Секунда — это угол, равный    части минуты. Минуты обозначают знаком  ‘ ,  a секунды — знаком  » .  Знак минут и секунд ставится в правом верхнем углу числа. Например, если угол имеет величину 50 градусов 34 минуты и 19 секунд, то пишут:

50°34‘19».

Свойства измерения углов

Если луч делит данный угол на две части (на два угла), то величина данного угла равна сумме величин двух полученных углов.

Рассмотрим угол  AOB:

Луч  OD  делит его на два угла:  ∠AOD  и  ∠DOB.  Таким образом,  ∠AOB = ∠AOD + ∠DOB.

Развёрнутый угол равен  180°.

Любой угол имеет определённую величину, большую нуля.

Как правильно определять углы — Инженер ПТО

Измерить угол – значит найти его величину. Величина угла показывает, сколько раз угол, выбранный за единицу измерения, укладывается в данном углу.

Обычно за единицу измерения углов принимают градус. Градус – это угол, равный части развёрнутого угла. Для обозначения градусов в тексте, используется знак °, который ставится в правом верхнем углу числа, показывающего количество градусов (например, 60°).

Измерение углов транспортиром

Для измерения углов используют специальный прибор – транспортир:

У транспортира две шкалы – внутренняя и внешняя. Начало отсчёта у внутренней и у внешней шкал располагается с разных сторон. Чтобы получить правильный результат измерения, отсчёт градусов должен начинаться с правильной стороны.

Измерение углов производится следующим образом: транспортир накладывают на угол так, чтобы вершина угла совпала с центром транспортира, а одна из сторон угла прошла через нулевое деление на шкале. Тогда другая сторона угла укажет величину угла в градусах:

Говорят: угол BOC равен 60 градусов, угол MON равен 120 градусов и пишут: ∠BOC = 60°, ∠MON = 120°.

Для более точного измерения углов используют доли градуса: минуты и секунды. Минута – это угол, равный части градуса. Секунда – это угол, равный части минуты. Минуты обозначают знаком ‘, a секунды – знаком

». Знак минут и секунд ставится в правом верхнем углу числа. Например, если угол имеет величину 50 градусов 34 минуты и 19 секунд, то пишут:

Свойства измерения углов

Если луч делит данный угол на две части (на два угла), то величина данного угла равна сумме величин двух полученных углов.

Рассмотрим угол AOB:

Луч OD делит его на два угла: ∠AOD и ∠DOB. Таким образом, ∠AOB = ∠AOD + ∠DOB.

Развёрнутый угол равен 180°.

Любой угол имеет определённую величину, большую нуля.

При отделочных работах и строительстве бывает нужна четкая геометрия: перпендикулярные стены и иные конструкции, требующие прямого угла в 90 градусов. Обыкновенный угольник не может позволить проверить или разметить углы со сторонами в несколько метров. Описываемый же метод превосходно подходит для разметки или проверки любых углов — длинна сторон не ограничена. Основной инструмент для измерений — рулетка.

Мы будем рассматривать точную разметку прямого угла, а также метод проверки уже размеченных углов на стенах и других объектах.

Теорема Пифагора

Теорема основана на утверждении, что у прямоугольного треугольника сумма квадратов длин катетов равна квадрату длины гипотенузы. В виде формулы записывается это так:

Стороны a и b — катеты, между которыми угол равен ровно 90 градусов. Следовательно, сторона c — гипотенуза. Подставляя в эту формулу две известные величины, мы можем вычислить третью, неизвестную. А следовательно можем размечать прямые углы, а также проверять их.

Теорема Пифагора известна еще под названием «египетский треугольник». Это треугольник со сторонами 3, 4 и 5, причем совершенно не важно, в каких единицах длинны. Между сторонами 3 и 4 — ровно девяносто градусов. Проверим данное утверждение вышеприведенной формулой: a²+b²=c² = (3×3)+(4×4) = 9+16 = (5×5) = 25 — все сходится!

А теперь применим теорему на практике.

Проверка прямого угла

Начнем с самого простого — проверки прямого угла с помощью теоремы Пифагора. Самым частым примером в отделке и строительстве является проверка

перпендикулярности стен. Перпендикулярные стены — это стены, расположенные друг к другу под прямым углом 90°.

Итак, берем любой проверяемый внутренний угол. На стенах (на одной высоте) или на полу отмечаем на обоих стенах отрезки произвольных длин. Длинна этих отрезков произвольная, по возможности нужно отмечать как можно больше, но чтобы между отметками на стенах удобно было мерить диагональ. Например, мы отметили 2,5 метра (или 250 см.) на одной стене и 3 метра (или 300 см.) на другой. Теперь длину отрезка каждой стены возводим в квадрат (умножаем саму на себя) и получившиеся произведения складываем. Выглядит это так: (2,5×2,5)+(3×3)=15,25 — это диагональ в квадрате. Теперь нужно извлечь из этого числа квадратный корень √15,25≈3,90 — 3,9 метра должна составлять диагональ между нашими отметками. Если измерение рулеткой показывает другую длину диагонали — проверяемый угол развернут и имеет отклонение от 90°.

Калькулятор расчета диагонали прямого угла

Извлечение квадратного корня никогда меня не привлекало — простому человеку не обойтись без калькулятора, к тому же, не на всех мобильных устройствах калькуляторы умеют извлекать его. Поэтому можно пользоваться упрощенным методом. Нужно лишь запомнить: у прямого угла со сторонами ровно 100 сантиметров, диагональ равна 141,4 см.

Таким образом, у прямого угла со сторонами 2 м. — диагональ равна 282,8 см. То есть на каждый метр плоскости приходится 141,4 см. У этого метода один недостаток: от измеряемого угла нужно откладывать одинаковые расстояния на обеих стенах и отрезки эти должны быть кратны метру. Не буду утверждать, но по моей скромной практике — это гораздо удобнее. Хотя не стоит забывать о первоначальном способе совсем — в некоторых случаях он очень актуален.

Сразу же возникает вопрос: какое отклонение от вычисленной длинны диагонали считать нормой (погрешностью), а какое нет? Если проверяемый угол с отмеченными сторонами по 1 м. будет 89°, то диагональ уменьшится до 140 см. Из понимания этой зависимости можно сделать объективный вывод, что погрешность диагонали 141,4 см.

в несколько миллиметров не даст отклонения в один целый градус.

Как проверить внешний угол? Проверка внешнего угла по сути не отличается, нужно лишь продлить линии каждой стены на полу (или земле, при помощи шнура) и получившийся внутренний угол измерить обычным способом.

Как разметить прямой угол рулеткой

Разметка может основываться как на общей теореме Пифагора, так и на принципе «египетского треугольника». Однако это только в теории линии просто чертятся на бумаге, «ловить» же все выбранные размеры растянутыми шнурами или линиями на полу — задача посложнее.

Поэтому я предлагаю упрощенный способ, основанный на диагонали 141,4 см. у треугольника со сторонами 100 см. Вся последовательность разметки изображена на картинках ниже. Важно не забывать: диагональ 141,4 см. нужно умножать на количество метров в отрезке А-Б. Отрезки А-Б и А-В должны быть равны и соответствовать целому числу в метрах. Картинки увеличиваются по клику!

Как разметить острый угол

Гораздо реже возникает надобность в создании острых углов, в частности 45°. Для формирования подобных фигур формулы более сложные, однако это не самое проблематичное. Гораздо сложнее свести все линии, начерченные или натянутые шнурами — дело это непрос

Как правильно измерять градус угла

Измерить угол

– значит найти его величину. Величина угла показывает, сколько раз угол, выбранный за единицу измерения, укладывается в данном углу.

Обычно за единицу измерения углов принимают градус. Градус – это угол, равный части развёрнутого угла. Для обозначения градусов в тексте, используется знак °, который ставится в правом верхнем углу числа, показывающего количество градусов (например, 60°).

Измерение углов транспортиром

Для измерения углов используют специальный прибор – транспортир:

У транспортира две шкалы – внутренняя и внешняя. Начало отсчёта у внутренней и у внешней шкал располагается с разных сторон. Чтобы получить правильный результат измерения, отсчёт градусов должен начинаться с правильной стороны.

Измерение углов производится следующим образом: транспортир накладывают на угол так, чтобы вершина угла совпала с центром транспортира, а одна из сторон угла прошла через нулевое деление на шкале. Тогда другая сторона угла укажет величину угла в градусах:

Говорят: угол BOC равен 60 градусов, угол MON равен 120 градусов и пишут: ∠BOC = 60°, ∠MON = 120°.

Для более точного измерения углов используют доли градуса: минуты и секунды. Минута – это угол, равный части градуса. Секунда – это угол, равный части минуты. Минуты обозначают знаком ‘, a секунды – знаком ”. Знак минут и секунд ставится в правом верхнем углу числа. Например, если угол имеет величину 50 градусов 34 минуты и 19 секунд, то пишут:

Свойства измерения углов

Если луч делит данный угол на две части (на два угла), то величина данного угла равна сумме величин двух полученных углов.

Рассмотрим угол AOB:

Луч OD делит его на два угла: ∠AOD и ∠DOB. Таким образом, ∠AOB = ∠AOD + ∠DOB.

Развёрнутый угол равен 180°.

Любой угол имеет определённую величину, большую нуля.

Люди обычно сталкиваются с транспортирами в математике, когда учатся в школе создавать точные геометрические фигуры. Возможно, у многих из них никогда больше не будет причин снова использовать эти приборы, тем не менее транспортиры имеют долгую историю применения в различных областях.

История изобретения

Происхождение этого математического инструмента восходит к жрецам в Египте и Вавилоне, которые установили меру углов в градусах, минутах и секундах. Однако до времён классической Греции тригонометрия не использовалась в математике.

Во втором веке до нашей эры астроном Гиппарх из Никии изобрёл тригонометрический стол, для измерения треугольников.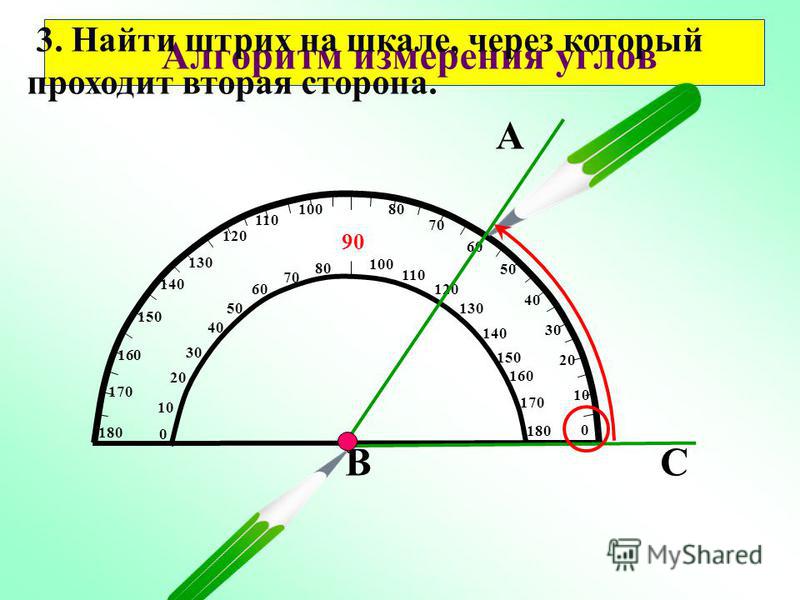 Затем Птолемей включил в свою великую астрономическую книгу «Альмагест» таблицу, с угловыми приращениями от 0 до 180°, с погрешностью менее 1/3600 единиц. Он также объяснил метод составления этой таблицы, и на протяжении всей книги приводил много примеров того, как вычислять с помощью неё неизвестные элементы фигур.

Птолемей также был автором, так называемой теоремы Менелая для решения сферических треугольников, и на протяжении многих веков его тригонометрия была основным пособием для астрономов.

Возможно, в то же время, учёные Индии также разработали тригонометрическую систему, основанную на функции синуса, которая, в отличие от используемого в настоящее время синуса, была не пропорцией, а длиной стороны, противоположной углу в прямом треугольнике этой гипотенузы. Индийские математики использовали разные значения для этого в своих таблицах.

Томас Бландевиль рассказал о приборе специально созданном, для рисования и измерения фигур в своём «Кратком описании универсальных карт» 1589 года. Как видно из названия, он применял его, чтобы править навигационные карты для использования в высоких широтах.

Другие европейские математики также описывали подобные приборы примерно в то же время. Независимо от того, кто первым придумал этот инструмент, к началу XVII века он вошёл в стандартную практику мореплавателей и геодезистов. К XVIII веку транспортиры начали появляться в учебниках по геодезии и геометрии.

Транспортиры в современном понимании возникли во второй половине XVIII века, когда такие учёные, как Джесси Рамсден и Георг Фридрих Брандер, усовершенствовали ранее созданные устройства.

В то время предпочтительными материалами для их изготовления были:

В первой половине XX века начали применять олово и целлулоид.

Называться транспортиром (рус.) прибор стал в 1610 году.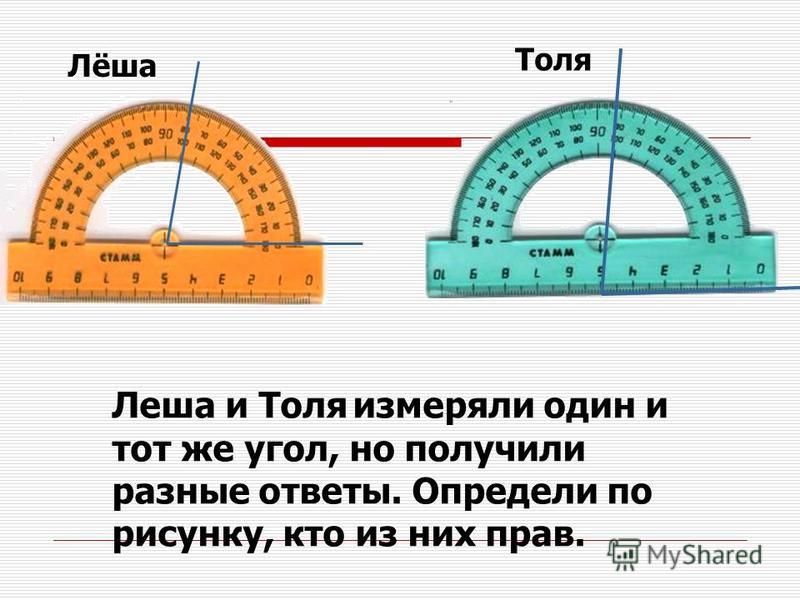 Термин произошёл от средневекового слова protractor, что означает «переносить», который, в свою очередь, произошел от латинского слова protrahere «тянуть вперёд».

Разновидности и использование

Транспортир — это простой гониометр для измерения или создания угла. Он выглядит как круглый или полукруглый диск с делением. Диск может быть изготовлен из пластика, прочной бумаги или листового металла. Типичными являются диаметры от 8 до 15 см и деления на 1° и 0,5°, при измерении также 0,5 Гон (новый градус). Точность составляет от 0,1 до 0,5° в зависимости от диаметра шкалы. Более точные приборы имеют поворотную рейку со шкалой (длина до миллиметра).

Частично из-за различного использования их изготавливают во многих формах: знакомый полукруг, а также круги, прямоугольники, квадраты или четверть круга (квадранты). Они также могут иметь различные диаметры. Их изготавливают из латуни, стали, дерева, слоновой кости или пластика. Самой распространённой формой является полукруг с ограничительной шкалой в 180 градусов.

Угловой транспортир — градуированный круглый инструмент с одной поворотной рукой; используется для измерения или разметки. В строительстве часто требуется отмерить угол в 90 градусов. Иногда прилагается шкала Вернье, чтобы дать более точные показания. Прибор широко применяется для изготовления архитектурных и механических чертежей, хотя его использование уменьшилось с появлением современного программного обеспечения для рисования.

Универсальные транспортиры скоса используются изготовителями инструментов; поскольку они делают измерения посредством механического контакта с предметом, то классифицируются как механические транспортиры.

Угловой транспортир применяется для того, чтобы измерить и проверить углы с очень жёсткими допусками. Он считывает до 5 угловых минут (5 или 1/12°) и может измерять от 0 до 360°.

Сегодня также применяются электронные приборы, которые обычно работают с поворотным датчиком. Кроме того, связанными с транспортиром приборами являются:

• теодолит;
• оптический транспортир в строительной промышленности и геодезии;
• инклинометр для определения уклонов и косвенной альтиметрии;
• секстант для навигации.

Измерение градусов угла

Для того чтобы научиться пользоваться транспортиром инструкция нужна на начальном этапе. Для его освоения достаточно нескольких минут и примеров (смотреть онлайн) того, как можно измерить и построить угол с помощью этого прибора.

Измерить угол, значит найти его величину. Углы разделяют на три типа: острый, тупой и прямой. Прямоугольный имеет 90 градусов. Все углы что имеют больше этого значения называются тупыми, и соответственно меньше 90 градусов называются острыми. Развёрнутый угол имеет 180 градусов.

Понимание того, что углы являются частями окружностей, полезно, потому что тогда конструкция транспортира обретает смысл. Поскольку полный круг имеет 360º, отдельный угол должен быть меньше этого числа, потому что он часть круга.

Алгоритм измерения следующий: для того чтобы измерить угол транспортиром необходимо приложить его центр верхней кромки линейки к вершине измеряемого угла. Вершина — это точка, в которой две из трёх сторон треугольника пересекаются.

Нижнюю планку (основание) транспортира нужно выставить горизонтально. Каждый транспортир имеет точку, спроектированную в центре основания, Эта средняя точка располагается на вершине угла, который должен быть измерен или нанесён на график. Другая сторона должна пересекать транспортир в одной из точек его дуги.

Если вторая сторона (линия) до дуги не доходит нужно продолжить её с помощью простой или масштабной линейки. То число, на шкале дуги, которое будет пересечено линией и есть величина угла в градусах.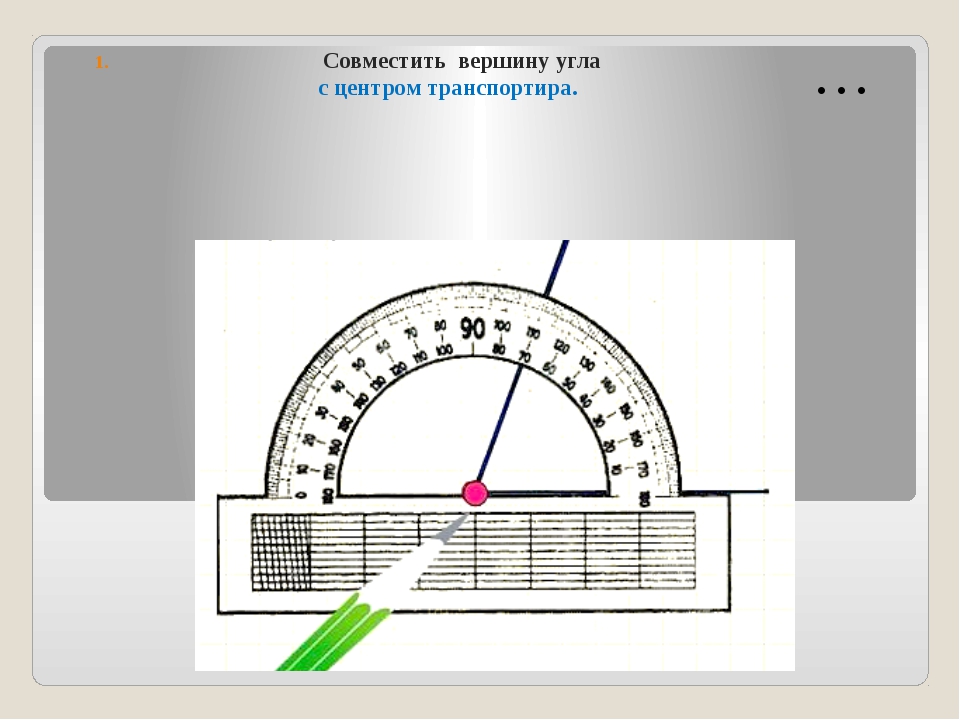

Для удобства на большинстве транспортиров сделано две шкалы, внутренняя и внешняя, которые отображают числа в каждой строке.

Построение угла

Берётся чистый лист бумаги в клетку. На нём карандашом отмечается точка, от которой проводиться прямая линия, как одна из сторон будущего угла. Эта черта служит для того, чтобы задать направление второй стороне. В простых упражнениях, для приобретения навыка построения угла, линия проводится горизонтально.

Центр основы транспортира располагается на любом из концов черты, который будет вершиной угла. Эта точка отмечается на бумаге карандашом. И именно к этому месту, внутри отверстия и присоединяется вершина угла, одна из сторон которого должна совпадать в горизонтальной плоскости с внутренней стороной линейки транспортира.

Затем на шкале отмечается необходимый градус. С внутренней стороны отверстия также обозначается точка возле этого градуса. И от вершины проводится прямая линия к этой точке. Таким образом, получается необходимый угол.

Для того чтобы правильно пользоваться транспортиром очень важно его выровнять, и точно прикладывать, для получения верных измерений.

Пересечённые линии в верхней части прямой кромки линейки должны совпадать с вершиной (конечной точкой), где соединяются два луча.

При отделочных работах и строительстве бывает нужна четкая геометрия: перпендикулярные стены и иные конструкции, требующие прямого угла в 90 градусов. Обыкновенный угольник не может позволить проверить или разметить углы со сторонами в несколько метров. Описываемый же метод превосходно подходит для разметки или проверки любых углов – длинна сторон не ограничена. Основной инструмент для измерений – рулетка.

Мы будем рассматривать точную разметку прямого угла, а также метод проверки уже размеченных углов на стенах и других объектах.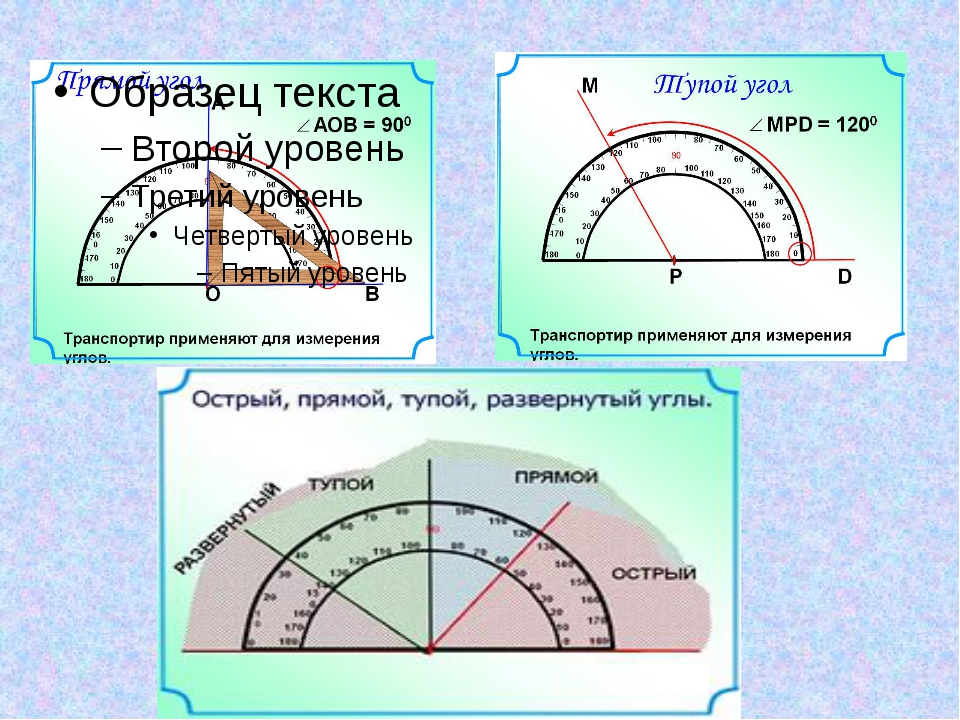

Теорема Пифагора

Теорема основана на утверждении, что у прямоугольного треугольника сумма квадратов длин катетов равна квадрату длины гипотенузы. В виде формулы записывается это так:

Стороны a и b – катеты, между которыми угол равен ровно 90 градусов. Следовательно, сторона c – гипотенуза. Подставляя в эту формулу две известные величины, мы можем вычислить третью, неизвестную. А следовательно можем размечать прямые углы, а также проверять их.

Теорема Пифагора известна еще под названием «египетский треугольник». Это треугольник со сторонами 3, 4 и 5, причем совершенно не важно, в каких единицах длинны. Между сторонами 3 и 4 – ровно девяносто градусов. Проверим данное утверждение вышеприведенной формулой: a²+b²=c² = (3×3)+(4×4) = 9+16 = (5×5) = 25 – все сходится!

А теперь применим теорему на практике.

Проверка прямого угла

Начнем с самого простого – проверки прямого угла с помощью теоремы Пифагора. Самым частым примером в отделке и строительстве является проверка перпендикулярности стен. Перпендикулярные стены – это стены, расположенные друг к другу под прямым углом 90°.

Итак, берем любой проверяемый внутренний угол. На стенах (на одной высоте) или на полу отмечаем на обоих стенах отрезки произвольных длин. Длинна этих отрезков произвольная, по возможности нужно отмечать как можно больше, но чтобы между отметками на стенах удобно было мерить диагональ. Например, мы отметили 2,5 метра (или 250 см.) на одной стене и 3 метра (или 300 см.) на другой. Теперь длину отрезка каждой стены возводим в квадрат (умножаем саму на себя) и получившиеся произведения складываем. Выглядит это так: (2,5×2,5)+(3×3)=15,25 – это диагональ в квадрате. Теперь нужно извлечь из этого числа квадратный корень √15,25≈3,90 – 3,9 метра должна составлять диагональ между нашими отметками. Если измерение рулеткой показывает другую длину диагонали – проверяемый угол развернут и имеет отклонение от 90°.

Калькулятор расчета диагонали прямого угла

Извлечение квадратного корня никогда меня не привлекало – простому человеку не обойтись без калькулятора, к тому же, не на всех мобильных устройствах калькуляторы умеют извлекать его. Поэтому можно пользоваться упрощенным методом. Нужно лишь запомнить: у прямого угла со сторонами ровно 100 сантиметров, диагональ равна 141,4 см. Таким образом, у прямого угла со сторонами 2 м. – диагональ равна 282,8 см. То есть на каждый метр плоскости приходится 141,4 см. У этого метода один недостаток: от измеряемого угла нужно откладывать одинаковые расстояния на обеих стенах и отрезки эти должны быть кратны метру. Не буду утверждать, но по моей скромной практике – это гораздо удобнее. Хотя не стоит забывать о первоначальном способе совсем – в некоторых случаях он очень актуален.

Сразу же возникает вопрос: какое отклонение от вычисленной длинны диагонали считать нормой (погрешностью), а какое нет? Если проверяемый угол с отмеченными сторонами по 1 м. будет 89°, то диагональ уменьшится до 140 см. Из понимания этой зависимости можно сделать объективный вывод, что погрешность диагонали 141,4 см. в несколько миллиметров не даст отклонения в один целый градус.

Как проверить внешний угол? Проверка внешнего угла по сути не отличается, нужно лишь продлить линии каждой стены на полу (или земле, при помощи шнура) и получившийся внутренний угол измерить обычным способом.

Как разметить прямой угол рулеткой

Разметка может основываться как на общей теореме Пифагора, так и на принципе «египетского треугольника». Однако это только в теории линии просто чертятся на бумаге, «ловить» же все выбранные размеры растянутыми шнурами или линиями на полу – задача посложнее.

Поэтому я предлагаю упрощенный способ, основанный на диагонали 141,4 см. у треугольника со сторонами 100 см. Вся последовательность разметки изображена на картинках ниже. Важно не забывать: диагональ 141,4 см. нужно умножать на количество метров в отрезке А-Б. Отрезки А-Б и А-В должны быть равны и соответствовать целому числу в метрах. Картинки увеличиваются по клику!

Как разметить острый угол

Гораздо реже возникает надобность в создании острых углов, в частности 45°. Для формирования подобных фигур формулы более сложные, однако это не самое проблематичное. Гораздо сложнее свести все линии, начерченные или натянутые шнурами – дело это непростое. Поэтому я предлагаю использовать упрощенный метод. Сначала размечается прямой угол 90°, а затем диагональ 141,4 делится на нужное количество равных частей. Например, чтобы получить 45°, диагональ нужно поделить пополам и от точки А провести линию через место деления. Таким образом мы получим два угла по 45 градусов. Если поделить диагональ на 3 части, то получится три угла по 30 градусов. Думаю алгоритм вам понятен.

Собственно я рассказал все, что мог рассказать, надеюсь все изложил понятным языком и у вас больше не возникнет вопросов как размечать и проверять прямые углы. Стоит добавить, что уметь делать это должен любой отделочник или строитель, ведь полагаться на строительный угольник небольшого размера – непрофессионально.

Измерение углов. Транспортир. Что такое транспортир? Правила измерения углов

Ответ оставил Гость

Транспортир – это инструмент для измерения градусного значения углов. В основном распространены транспортиры полукруглой формы, но есть и круглые транспортиры, составляющие 360 градусов. Если вы совсем не понимаете, как пользоваться транспортиром, а потому даже боитесь взять его в руки, прочитайте эту статью! Это совсем несложно. Немного простых шагов, и вы уже не будете бояться одного только вида этого инструмента.Метод 1 из 3: Как пользоваться транспортиром1Во-первых, нужно понять, что представляет из себя этот инструмент.Транспортир имеет полукруглую форму с небольшим отверстием в середине. Это отверстие называется точкой отсчета. Точку отсчета нужно совместить с вершиной треугольника. 2Основание транспортира нужно разместить так, чтобы оно было параллельно катету треугольника или стороне угла. Выберите сторону треугольника, которая будет базовой, с этой стороной нужно совместить основание транспортира. Не путайте базовую линию угла и основание транспортира! 3Вы совместили точку отсчета с вершиной угла, а основание транспортира с катетом. Теперь вы можете смело измерить угол. Второй катет треугольника будет указывать на шкалу с цифрами на полуокружности транспортира. Важно не запутаться с этими цифрами. Удобнее всего использовать двусторонний транспортир, у которого с обеих сторон есть шкала с цифрами.Как вы сами понимаете, чем больше угол (то есть «тупее»), тем больше градусное значение. К примеру, полный круг составляет 360 градусов, а угол может составлять максимум 180 градусов (если угол «развернутый», то есть представляет из себя просто прямую). Градусы отмечены на полуокружности транспортира сверху.Самые маленькие углы (то есть «острые») будут составлять меньше 90 градусов. А более развернутые (то есть «тупые») – больше 90 градусов.Совместите центральную точку (или точку отсчета) с вершиной угла, который вы хотите измерить. Постарайтесь как-то зафиксировать транспортир на этом месте с помощью карандаша или другого предмета. Затем поверните транспортир таким образом, чтобы одна из сторон угла совпадала с основанием транспортира, при этом полуокружность с градусной шкалой должна смотреть вверх. 2Теперь посмотрите, на какое число на полуокружности указывает вторая сторона угла. Если она не доходит до полуокружности транспортира, аккуратно продлите ее карандашом, чтобы она пересекала полуокружность транспортира. Посмотрите, через какое число проходит эта линия.Если вы не можете продлить линию, но она все равно не доходит до полуокружности транспортира, возьмите кусочек бумаги или линейку и совместите ее с той стороной, которая не доходит до полуокружности. Таким образом, линейка должна «продлевать» вторую сторону угла до пересечения с полуокружностью, на которой указаны градусы.Метод 3 из 3: Как начертить угол с помощью транспортира1Начертите линию. Это будет базовая линия, по которой вы будете ориентироваться, чтобы начертить вторую линию. Будет намного удобнее, если базовая линия будет располагаться горизонтально. 2Затем отметьте точку на этой линии, которая станет вершиной вашего угла. Совместите эту точку с точкой отсчета на транспортире. 3Теперь совместите базовую линию угла с основанием транспортира.Затем посмотрите на полуокружность транспортира и выберите нужное вам градусное значение. Нарисуйте на бумаге точку рядом с этим значением, к этой точке вы поведете вторую линию из вершины угла. 4Отложите транспортир в сторону. Теперь возьмите линейку и соедините вершину угла и точку, которую вы нарисовали возле нужного вам градусного значения. Готово! У вас получился угол с заданным градусным значением.

Еще в школе каждый человек сталкивался с такой вещью, как транспортир. Но, к сожалению, далеко не каждый, как в школьное время, так и уже в старшем возрасте, знает, как правильно им пользоваться. Данная инструкция научит каждого правильно пользоваться этим предметом.

Начнем, пожалуй, с того, что же такое транспортир. Транспортир – это инструмент для измерения градусного значения углов. Чаще всего такой инструмент имеет полукруглую форму. Но есть и исключения, а именно транспортиры, которые имеют полностью круглую форму (360 градусов).

Как правильно пользоваться транспортиром

• Для начала необходимо понять, что представляет из себя данный инструмент. Он являет собой полукруглый предмет (как уже было сказано выше, может быть и круглый) с небольшим отверстием в середине, которое называется точкой отсчета. Именно последнее (точку отсчета) нужно совместить с вершиной треугольника.
• Дальше для измерения необходимого угла, необходимо основание транспортира разместить параллельно стороне угла или катету треугольника. Для этого нужно выбрать сторону треугольника (она будет базовой, именно с этой стороной нужно совместить основание транспортира). Не стоит путать базовую линию угла и основание транспортира (это совершенно разные вещи).
• Как только вы совместили точку отсчета с вершиной угла, а основание транспортира с катетом, можно смело измерить угол. Тогда второй катет треугольника будет указывать на шкалу с цифрами на полуокружности транспортира. Главное – это не запутаться с цифрами, ведь сделав это, вы допустите ошибку в измерении необходимого угла.
• Стоит понимать, что чем больше (тупее) угол, тем больше его градусное значение. Угол максимально может составить 180 градусов.
• Самые маленькие (острые) углы могут составлять только меньше 90 градусов, все, которые будут больше этого значения уже считаются большими (тупыми).

Как правильно измерить градусное значение угла транспортиром

Для этого необходимо сделать следующие действия:

• Центральную точку (точку отсчета) необходимо совместить с вершиной угла, который необходимо измерить. Транспортир необходимо зафиксировать на данном месте с помощью ручки, карандаша или любого другого предмета. После этого его необходимо повернуть таким образом, чтобы одна из сторон угла совпала с основанием транспортира (полуокружность с градусной шкалой должна смотреть вверх).
• Теперь необходимо посмотреть, на какое число на полуокружности указывает вторая сторона угла (она должна пересекать полуокружность транспортира). Необходимо посмотреть, через какое число проходит эта линия.
• Если линию продлить невозможно (она все равно не доходит до полуокружности транспортира), следует взять кусочек бумаги или линейку и совместить ее с той стороной, которая не доходит до полуокружности. В таком случае, линейка должна “продлить” вторую сторону угла до пересечения с полуокружностью, на которую указаны градусы.

Как правильно начертить угол при помощи транспортира

• Для начала необходимо начертить линию с помощью транспортира. Такая линия будет базовой. Именно по ней вы будете ориентироваться, чтобы начертить вторую. Для лучшего удобства ее нужно расположить горизонтально.
• На этой линии необходимо отметить точку, которая будет вершиной вашего угла. Такую точку необходимо совместить с точкой отсчета на транспортире.
• Далее необходимо совместить базовую линию угла с основанием транспортира. После этого следует посмотреть на полуокружность транспортира и выбрать необходимое градусное значение. На бумаге следует нарисовать точку рядом с этим значением. К такой точке необходимо будет провести вторую линию из вершины угла.
• После этого можно смело отложить транспортир в сторону.
• Теперь нужно взять в руки линейку и соединить вершину угла и точку, которая уже была нарисована возле нужного вам градусного значения.

Дело сделано! Вы получили угол с необходимым для вас градусным значением. В итоге, хотелось бы сказать, что пользоваться транспортиром достаточно просто, если грамотно использовать все эти советы. Но если же вам удалось немного запутаться с градусными шкалами, стоит помнить, что они абсолютно одинаковы, только идут в противоположных направлениях для удобства использования транспортира.



Углы и измерение углов

Угловые размеры определяют положение плоскостей, осей, линий, центров отверстий и т. д. Угловые размеры бывают зависимые и назависимые.
Независимые углы не связаны с другими параметрами изделия; зависимые углы определяются основными параметрами изделий, к которым они относятся.

В качестве единицы измерения плоских углов Международной системой единиц (СИ) принят радиан — угол между двумя радиусами круга, вырезающими на его окружности дугу, длина которой равна радиусу данного круга.
Измерение углов в радианах на практике связано с значительными трудностями, так как ни один из современных угломерных приборов не имеет градуировки в радианах.
По этой причине в машиностроении для угловых измерений в основном применяются внесистемные единицы: градус, минута и секунда. Эти единицы связаны между собой следующими соотношениями:

• 1 рад = 57°17׳45״ = 206 265″
• 1° = π/180 рад = 1,745329 × 10 -2 рад;
• 1‘ = π /10800 рад = 2,908882 × 10 -1 рад;
• 1” = π/648000 рад = 4,848137 × 10 -6 рад.

Значение угла при измерении определяют сравнением его с известным углом. Известный угол может быть задан так называемыми жесткими (с постоянным значением угла) мерами — аналогами формы элементов детали: угловыми мерами, угольниками, угловыми шаблонами, коническими калибрами, многогранными призмами.
Измеряемый угол можно сравнивать также с многозначными угломерными штриховыми мерами и различными видами круговых и секторных шкал. Еще одним методом получения известного угла является его расчет по значениям линейных размеров на основании тригонометрических зависимостей.

В соответствии с этим классификацию методов измерений углов производят в первую очередь по виду создания известного угла: сравнением с жесткой мерой, сравнением с штриховой мерой (гониометрические методы) и тригонометрическими методами (по значениям линейных размеров).

При сравнении углов с жесткой мерой отклонение измеряемого угла от угла меры определяют по просвету между соответствующими сторонами углов детали и меры, по отклонению показаний прибора линейных размеров, измеряющих несовпадение этих сторон или при контроле «по краске», т.е. по характеру тонкого, слоя краски, перенесенного с одной поверхности на другую.

В приборах для гониометрических измерений имеются штриховая угломерная шкала, указатель и устройство для определения положения сторон угла. Это устройство связано с указателем или шкалой, а измеряемая деталь — соответственно со шкалой или указателем. Определение положения сторон угла можно производить как контактным, так и бесконтактным (оптическим) способом. При соответствующих измеряемому углу положениях узлов прибора определяют угол относительного поворота шкалы и указателя.

При косвенных тригонометрических методах определяют линейные размеры сторон прямоугольного треугольника, соответствующего измеряемому углу, и по ним находят синус или тангенс этого угла (координатные измерения). В других случаях (измерение с помощью синусных или тангенсных линеек) воспроизводят прямоугольный треугольник с углом, номинально равным измеряемому, и устанавливая его как накрест лежащий с измеряемым углом, определяют линейные отклонения от параллельности стороны измеряемого угла основанию прямоугольного треугольника.

При всех методах измерений углов должно быть обеспечено измерение угла в плоскости, перпендикулярной к ребру двугранного угла. Перекосы приводят к погрешности измерения.

При наличии наклона плоскости измерения в двух направлениях погрешность измерения угла может быть и положительной и отрицательной. При измерениях малых углов эта погрешность не превысит 1% значения угла при углах наклона плоскости измерения до 8° . Такая же зависимость погрешности измерения угла от углов перекоса получается и в случаях неточного базирования деталей на синусной линейке, несовпадения направления ребра измеряемого угла или оси призмы с осью поворота на гониометрических приборах (при фиксации положения граней по автоколлиматору), при измерениях с помощью уровней и т.п.

Угол наклона плоскостей обычно определяется уклоном, численно равным тангенсу угла наклона.
Малые значения уклонов часто указывают в микрометрах на 100 мм длины, в промилле или миллиметрах на метр длины (мм/м ).
Например, в мм/м указывается цена деления уровней. Пересчет уклонов в угол обычно производится по приближенной зависимости: уклон 0,01 мм/м (или 1 мкм/100 мм ) соответствует углу наклона в 2 ″ (погрешность подсчета угла по этой зависимости составляет — 3% ).

Как было показано выше в машиностроении в зависимости от используемых средств и методов различают три основных способа измерения углов :

Сравнительный метод измерения углов с помощью жестких угловых мер. При этом измерении определяется отклонение измеряемого угла от угла меры.

Абсолютный гониометрический метод измерения углов, при котором измеряемый угол определяется непосредственно по угломерной шкале прибора.

Косвенный тригонометрический метод: угол определяется расчетным путем по результатам измерения линейных размеров (катетов, гипотенузы), связанных с измеряемым углом тригонометрической функцией (синусом или тангенсом).

Сравнительный метод измерения углов обычно сочетается с косвенным тригонометрическим методом, последним определяется разница сравниваемых углов в линейных величинах на определенной длине стороны угла.



Угловые призматические меры и угольники

Угловые призматические меры служат для хранения и передачи единицы плоского угла. Их применяют для проверки шаблонов и угловых размеров различных изделий; для градиуровки угломерных приборов, а также для непосредственных измерений.
Угловые меры, предназначенные для проверки угломерных приборов и рабочих мер, называют образцовыми .

По точности аттестации образцовые угловые меры делят на четыре разряда (1,2,3 и 4 ). Предельные погрешности аттестации рабочих углов не должны превышать для угловых мер 1 -го разряда — ±0,5 ”; 2 -го разряда — ±1 ”; 3 -го — ±3 ”; 4-го — ±6 ”.
Угловые меры собирают в блоки с помощью специальных державок.

Контроль углов угольниками осуществляют, оценивая просвет между угольником и контролируемой деталью на глаз, или сравнивают с образцовой щелью, созданной с помощью концевых мер длины и лекальной линейки.
При использовании крупных угольников просвет оценивают с помощью щупов.
Погрешность проверки углов угольником зависит от погрешности самого угольника, длины сторон угла, по которой производится проверка, и других факторов.

Угломеры с нониусами

Угломеры с нониусами применяют для измерения профиля угла на деталях контактным методом с отсчетом по угловому нониусу с точностью 2 » и 5 «. Состоит угломер из круглого угломерного диска, скрепленного с корпусом зажимной гайкой. На основании смонтированы установочная планка и нониус с нанесенными 30 делениями с двух сторон от нулевого штриха; каждое деление соответствует 2 мин .
Линейка с лицевой стороны имеет продольный ласточкообразный паз, по которому перемешается (в процессе установки линейки на угол) хвостовик прижима.

При измерении угломер накладывают на проверяемую плоскость детали так, чтобы линейка и рабочая плоскость корпуса были совмещены со сторонами измеряемого угла. Целое число градусов отсчитывают по шкале диска до нулевого деления (штриха) нониуса. Затем определяют деление нониуса, совпадающего с делениями основной шкалы (диска).
После этого определяют по нониусу сколько минут и градусов совпадают с делениями нониуса.

Оптический угломер

В корпусе оптического угломера закреплен стеклянный диск со шкалой, имеющей деления в градусах и минутах. Цена малых делений 10 «. С корпусом жестко скреплена основная (неподвижная) линейка. На диске смонтированы лупа, рычаг и укреплена подвижная линейка.
Под лупой параллельно стеклянному диску расположена небольшая стеклянная пластинка, на которой нанесен указатель, ясно видимый через окуляр. Линейку можно перемещать в продольном направлении и с помощью рычага закреплять в нужном положении.

Во время поворота линейки в ту или другую сторону будет вращаться в том же направлении диск и лупа. Таким образом, определенному положению линейки будет соответствовать вполне определенное положение диска и лупы. После закрепления линеек зажимным кольцом через лупу отсчитывают показания угломера.
Оптическим угломером можно измерять углы от 0 до 180 °. Допускаемые погрешности показания оптического угломера ±5 «.

Индикаторный угломер

В индикаторном угломере обычная шкала и нониус заменены индикаторным циферблатом. Отсчет угловых размеров производится по показаниям стрелки на большой шкале через 10 °. Цена деления 5 «, предел измерения угломера 0…360 °.

Портативный оптический угломер-шаблон

Портативный оптический угломер-шаблон предназначен для проверки профиля резцов. Он состоит из стандартной восьмикратной лупы, неподвижно закрепленной на прозрачном диске из органического стекла. Вокруг оси, запрессованной в этот диск, свободно поворачивается стальной диск, по периметру которого с высокой точностью выполнены шаблоны наиболее часто встречающихся в практике углов, радиусов и кривых. Нужный профиль шаблона накладывают на затачиваемый резец и под лупой проверяют точность доводки.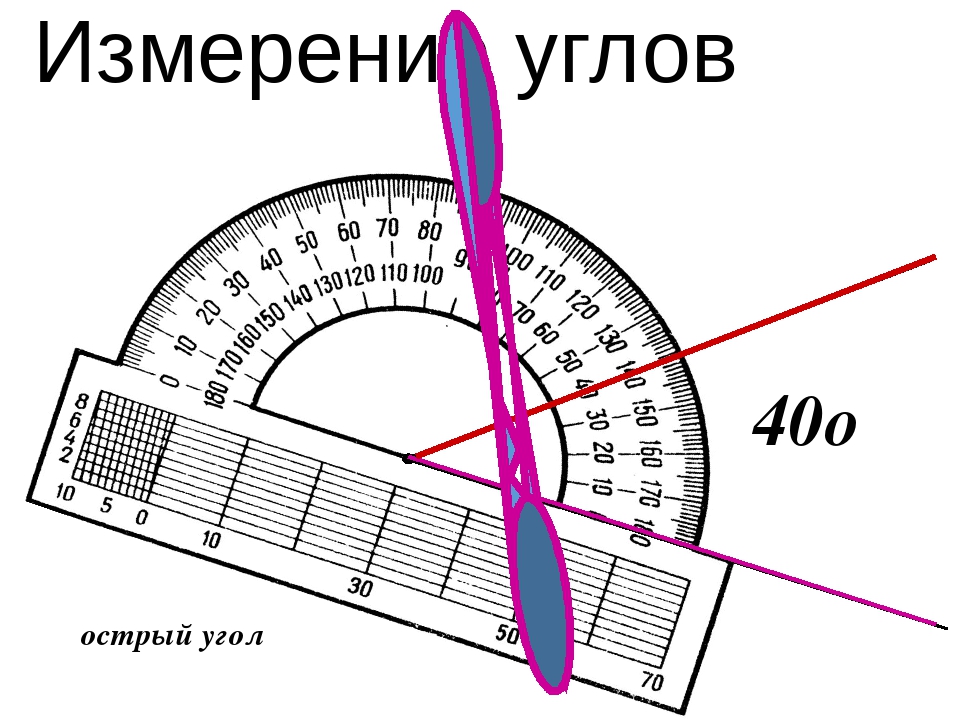
Прибор отличается точностью и удобством, так как им можно пользоваться непосредственно на рабочем месте.



Транспортир представляет собой геометрический инструмент, используемый для измерения углов.

Как выглядит транспортир

Основные и обязательные части транспортира — два ключевых элемента. Первый из них — линейка, разделенная на сантиметровые деления. При этом такая линейка обычно снабжена обозначением точки начала отсчета, которая используется в процессе измерений. Второй элемент транспортира — угломерная шкала, представляющая собой полукруг, обыкновенно включающий деления от 0 до 180°. При этом существуют модифицированные модели транспортиров, которые имеют полную круговую шкалу, то есть позволяют измерять углы величиной от 0 до 360° градусов.

Каждая угломерная шкала содержит линейку значений величины углов как в прямом, так и в обратном направлении. Это позволяет использовать транспортир для измерения как острых, так и тупых углов.

Материалы, применяемые для изготовления транспортиров, могут быть самыми различными. Самыми распространенными вариантами таких материалов являются пластик и металл. Дерево в настоящее время используется для этих целей несколько реже, поскольку такие транспортиры обычно имеют большую толщину и несколько менее удобны в использовании.

Точность измерений каждого инструмента находится в прямой зависимости от его размера. Так, более крупные транспортиры позволяют измерять углы с большей точностью, а небольшие инструменты дают лишь приблизительное представление о величине измеряемого угла.

Как использовать транспортир

При помощи транспортира можно решать две основные задачи: измерение углов и построение углов. Так, для измерения угла необходимо поместить его вершину в точку начала отсчета, обозначенную на линейке транспортира. Затем необходимо обратить внимание на то, чтобы сторона угла, направленная на угломерную шкалу, пересекала ее. В случае, если длина этой стороны оказывается недостаточной, следует продлить ее до пересечения угломерной шкалы.

После этого нужно посмотреть, на каком значении сторона угла пересекает указанную шкалу. В случае, если измерению подвергается острый угол, искомое значение будет меньше 90°, а при измерении тупого угла следует пользоваться той частью шкалы, которая содержит деления, превышающие 90°.

Аналогичным образом осуществляется построение углов при помощи транспортира. Сначала следует провести линию, которая будет представлять собой одну из сторон, а ее , которое станет вершиной, поместить в точку отсчета. Затем на угломерной шкале точкой нужно отметить нужную величину угла, который может быть как острым, так и тупым. После этого, убрав транспортир, соедините вершину будущего угла с проставленной точкой: в результате вы получите искомый угол.

Физики научились правильно измерять углы смачивания

M. Callies and D. Quéré / Soft Matter, 2005

Физики разработали схему надежного измерения краевых углов при смачивании водой поверхностей с разным типом микрорельефа и степенью гидрофобности. Оказалось, что лучше всего для точного определения углов смачивания использовать сидячую каплю, объем которой сначала медленно увеличивается, а потом уменьшается обратно. При этом, если правильно проводить эксперимент, то время одного полного измерения составит до 2 часов, пишут ученые в Nature Protocols. 

Один из основных параметров, характеризующих смачивание поверхностей жидкостью — это краевой угол, то есть угол, который образуется на стыке твердой, жидкой и газовой фаз между твердой поверхностью и касательной к поверхности жидкости.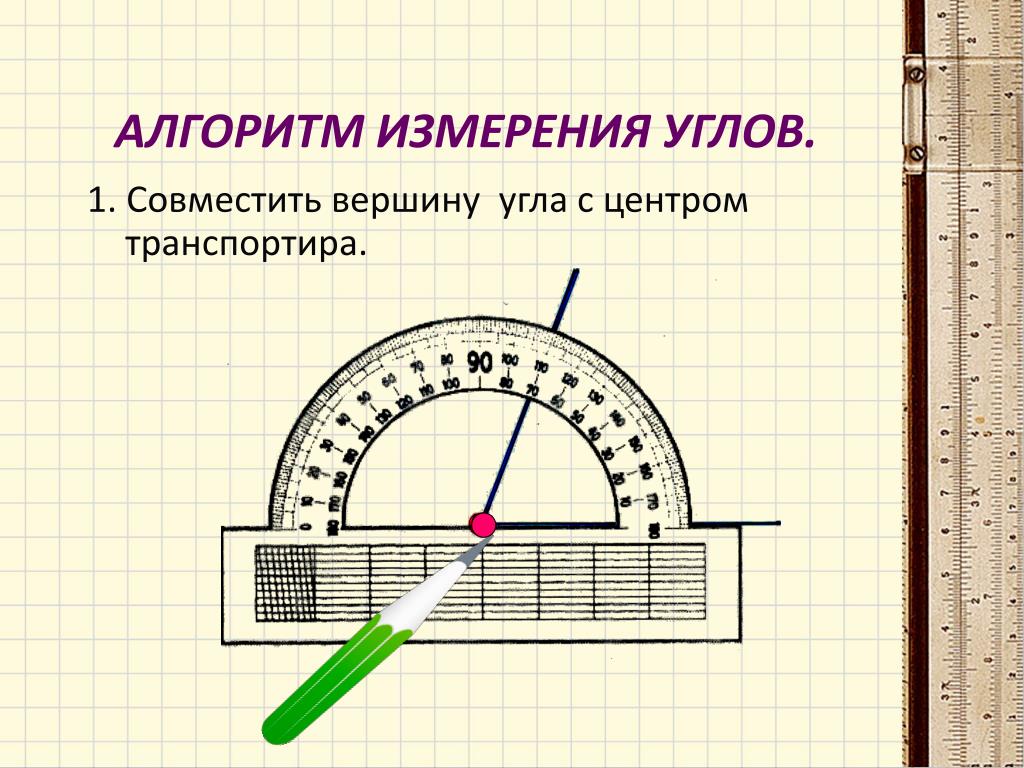 Для идеальной (гладкой и химически однородной) поверхности этот угол определяется соотношением Юнга, связывающим поверхностные энергии на трех межфазных границах (жидкость-твердое, жидкость-газ и твердое-газ). В случае смачивания поверхностей водой, если этот угол меньше 90 градусов, то поверхность называют гидрофильной, если больше — гидрофобной.

Угол смачивания — угол между касательной к поверхности капли в точке контакта и самой поверхностью. Слева направо угол смачивания уменьшается

Wikimedia Commons

Казалось бы, измерение этого угла — довольно простая процедура: нужно просто поместить на поверхность каплю жидкости, сфотографировать ее и измерить угол между двумя лучами на фотографии. Однако для реальных поверхностей эта задача оказывается не так проста, как кажется на первый взгляд. Во-первых, из-за неоднородности рельефа и химического состава поверхности этот угол для каждой поверхности может принимать не единственное значение, а множество значений в определенном диапазоне. Это явление называет гистерезисом краевого угла, а минимальный и максимальный краевые углы в этом диапазоне — соответственно, углами оттекания (receding angle) и натекания (advancing angle). Во-вторых, внутри этого диапазона между максимальным и минимальным значениями возможно существование нескольких дополнительных метастабильных состояний. Выбрать из них нужное, соответствующее глобальному минимуму энергии обычно бывает очень непросто, что приводит к систематическим ошибкам, как при измерении краевого угла в наиболее устойчивом состоянии, так и при определении углов натекания и оттекания.

Схема зависимости свободной энергии Гиббса от значения краевого угла для идеальной поверхности (слева) — с единственным минимумом, и для реальной шероховатой поверхности (справа) — с большим количеством локальных минимумов

T.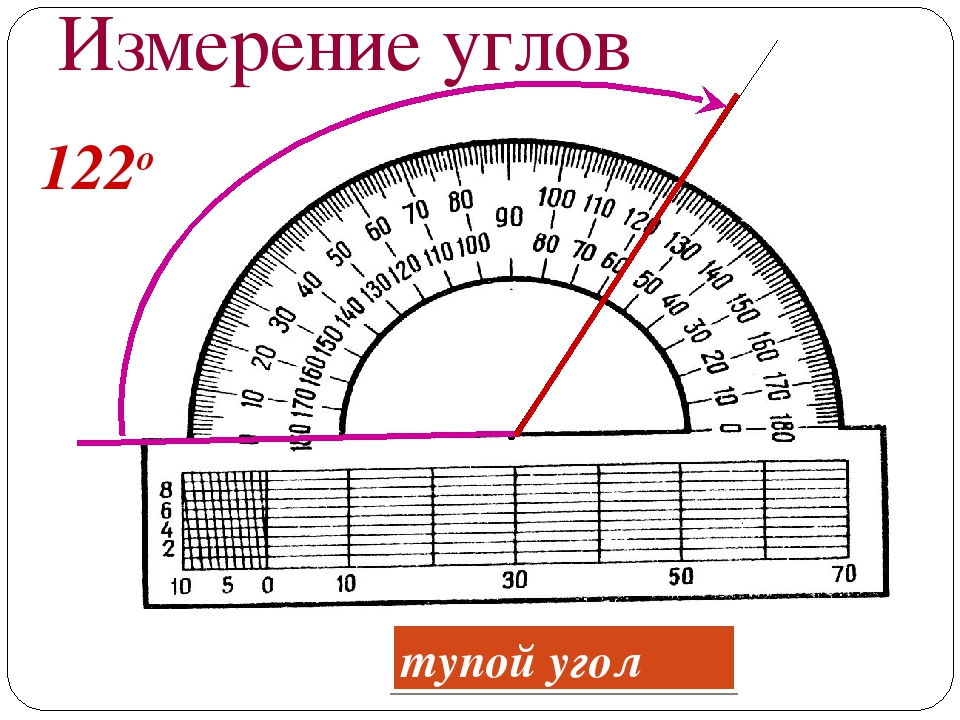 Huhtamäki et al./ Nature Protocols, 2018

Физики из Финляндии и Китая под руководством Робина Раса (Robin H. A. Ras) из Университета Аалто проанализировали все известные способы определения краевых углов и разработали общую схему проведения наиболее надежных измерений. Самым точным способом оказался метод сидячей капли, при котором капля помещается на исследуемую поверхность. Внутрь капли при этом помещается иголка шприцевого насоса, через которую можно закачивать и откачивать жидкость. После этого объем капли сначала медленно увеличивают, а потом — уменьшают обратно. Такой цикл повторяется многократно и контролируя все стадии процесса и измеряя динамику изменения краевого угла, можно получить необходимые значения.

Схема последовательных состояний капли во время измерения

T. Huhtamäki et al./ Nature Protocols, 2018

Этот метод оказался более надежным по сравнению с другими популярными способами измерения гистерезиса краевого угла — например, постепенным наклоном поверхности до того момента, как капля начнет с нее соскальзывать, или вытягиванием пластинки из объема жидкости.

В результате ученые нашли оптимальную скорость увеличения объема (от 0,05 до 2 микролитров в секунду в зависимости от стадии процесса), а также определили наиболее подходящий объем капли, который позволяет точно измерить углы оттекания и натекания на разных поверхностях. Оказалось, что для разных соотношений измеряемых углов этот объем может меняться почти на порядок — от 20 до 150 микролитров.

Оптимальный объем капли для измерения различных значений краевых углов оттекания и натекания

T.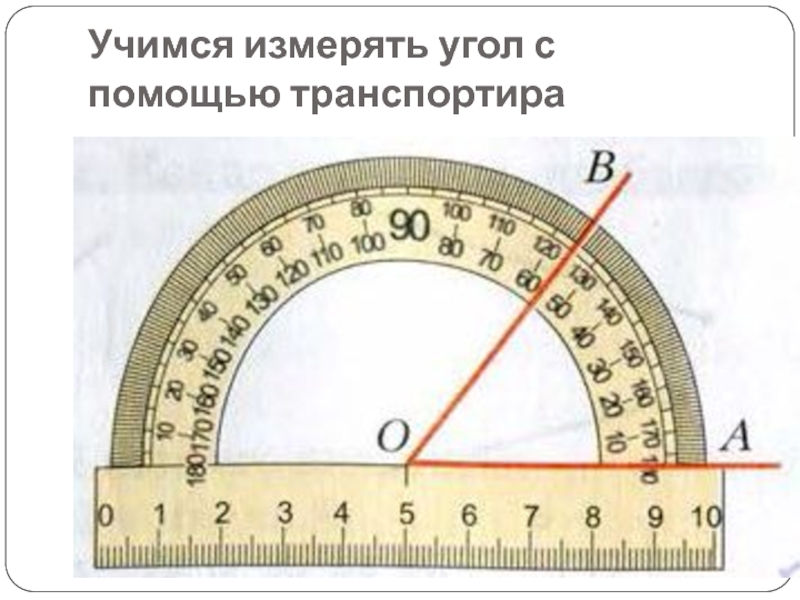 Huhtamäki et al./ Nature Protocols, 2018

Кроме того, ученые сформулировали рекомендации для настроек параметров съемки: увеличения, контрастности изображения и скорости записи, — а также описали возможные проблемы, которые могут возникать при измерении краевых углов на различных типах поверхности и предложили способы их решения.

Полное измерение параметров смачивания по предложенной схеме составит от одного до двух часов, а однократное определение углов оттекания и натекания — около 15 минут. Ученые отмечают, что пока предложенный метод был отработан только для смачивания однородных поверхностей водой, однако он может использоваться и для других жидкостей.

Стоит отметить, что из-за неоднородностей исследуемых поверхностей часто и значения краевых углов распределены по ним очень неравномерно. Чтобы определить, как параметры, определяющие смачивание поверхностей распределены по поверхности, физики разработали специальный микроскоп, чувствительным зондом которого служит капля жидкости.

Александр Дубов

Что такое Угол? Определение, виды, как обозначают? Примеры

Определение угла

Угол — это простая геометрическая фигура. Определение угла напрямую связано с понятием луча.

Луч — прямая линия, у которой есть начало, но нет конца, и продолжается она только в одну сторону.

Если нам дана прямая a на плоскости, и на ней есть некоторая точку O — выходит, что прямая разделена точкой на две части, каждая из которых является лучом с началом в точке O.

Луч можно обозначить одной строчной буквой латинского алфавита или двумя прописными. Например, вот так:

Угол — часть плоскости между двумя линиями, исходящими из одной точки. Каждая сторона угла является лучом, а вершина — общим началом сторон.

В математике существует специальный символ для обозначения угла, вот он: ∠.

Если стороны угла названы малыми латинскими буквами, то их записывают после символа. Например, так: ∠ab или ∠ba.

Если стороны угла названы большими буквами, то обозначение угла будет состоять из символа и трех букв, при этом вершина всегда записывается в центре. При сторонах угла OA и OB название угла запишем так: ∠AOB и ∠BOA.

Иногда можно встретить обозначение в виде цифр — так тоже можно.

Для наглядности — все способы обозначения углов:

Что такое вершина и стороны угла:

• Стороны угла — лучи, из которых состоит угол.
• Вершина угла — общее начало сторон угла.

Биссектриса — это луч, который исходит из вершины угла и делит его на два равных угла.

Так как угол делит плоскость на две части, одна будет внутренней областью угла, а другая — внешней областью угла. Вот так:

При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.

Единица измерения углов — градусы. Символ для обозначения градуса угла: °.

Определение смежных и вертикальных углов

Смежные углы — это пара углов, у которых одна сторона общая, а две другие стороны лежат на одной прямой. Таким образом два смежных угла составляют развернутый угол. Общая сторона двух смежных углов называется наклонной к прямой, на которой лежат другие стороны, при условии, что смежные углы не равны.

Вертикальные углы — это пара углов, у которых есть общая вершина, при этом стороны одного угла составляют продолжение сторон другого угла.

При пересечении прямых получается четыре пары смежных и две пары вертикальных углов. Вот как это выглядит:

Виды углов

Есть разные типы углов и у каждого своё название:

• острый
• прямой
• тупой
• развернутый
• выпуклый
• полный

Различать виды углов в геометрии важно. Определять можно на глаз или с помощью линейки.

Острый угол — это угол, который меньше прямого угла, то есть < 90°.

Прямой угол — это угол, стороны которого перпендикулярны друг другу. Прямой угол всегда равен половине развернутого угла, то есть = 90°.

Если два смежных угла равны между собой, то каждый из них является прямым. Для удобства прямой угол обозначается уголком. Вот так:

На картинке изображены два прямых угла ∠AOC и ∠COB. Общая сторона OC перпендикулярна прямой AB, а точка O — основание перпендикуляра.

Развернутый угол — это открытый угол, который образован двумя лучами и равен сумме двух прямых углов. Развернутый угол равен 180°. Как выглядит развернутый угол показано на первой картинке.

Неразвернутый угол — это любой угол, который не является развернутым, то есть не равен 180°.

Тупой угол — это угол, который больше прямого угла, но меньше развернутого:
90° < тупой угол < 180°.

Выпуклый угол — это угол, который больше развернутого угла, но меньше полного:
180° < выпуклый угол < 360°.

Полный угол — это угол, обе стороны которого совпадают с одним лучом. Он равен сумме четырех прямых углов, то есть = 360°.

Прилежащие углы — это пара углов с общей вершиной и стороной, другие стороны при этом лежат по разные стороны от общей стороны.

На картинке мы видим два прилежащих угла ∠AOB и ∠BOC, общую вершину O и общую сторону OB.

Можно сформулировать определение по-другому: если из вершины любого угла провести луч, разделяющий угол на два, то образованные углы будут прилежащими.

Чтобы найти угол, который разделен лучом, нужно сложить полученные углы: ∠AOB = ∠AOC + ∠COB. Из этого можно выделить следующие верные разности:

• ∠AOC = ∠AOB — ∠COB,
• ∠COB = ∠AOB — ∠AOC.

Сравнение углов

Для сравнения углов можно использовать самый простой способ из программы 4 класса — метод наложения.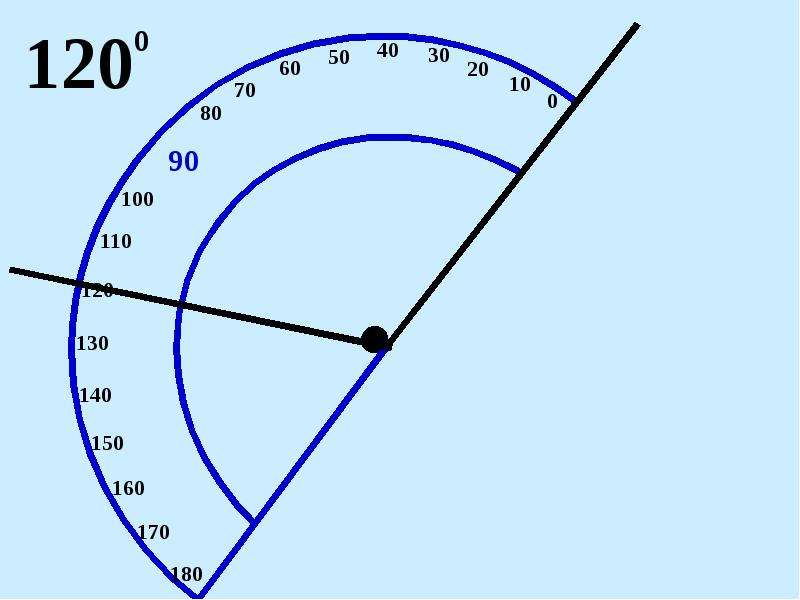 Для этого нужно совместить две вершины и сторону одного угла со стороной другого. Если стороны заданных углов совпадут, значит углы равные. Если нет, то угол, который лежит внутри другого, будет меньшим. Здесь два наглядных примера с равными и неравными углами:

При этом развернутые углы всегда являются равными.

Совмещение углов ∠𝐴𝐵𝐶 и ∠𝑀𝑁𝐾 происходит следующим образом:

 

1. Вершину 𝐵 одного угла совмещаем с вершиной 𝑁 другого угла.


2. Сторону 𝐵𝐴 одного угла накладываем на сторону 𝑁𝑀 другого угла так, чтобы стороны 𝐵𝐶 и 𝑁𝐾 располагались в одном направлении.

Если совпадут и другие стороны, то углы равны: ∠𝐴𝐵𝐶 = ∠𝑀𝑁𝐾.

Если нет, то один угол — меньше другого: ∠𝐴𝐵𝐶<∠𝑀𝑁𝐾.

Сравнить углы можно также, измерив их величины. Для этого понадобится специальный инструмент для построения и измерения углов — транспортир. Вот, как он выглядит:

Как правильно измерять углы

Измерение углов похоже на измерение отрезков: нужно сравнить их с углом, принятым за единицу измерения. В геометрии обычно за единицу измерения принимают градус — угол, равный 1/180 части развернутого угла. Обозначается — 0.

Градусная мера угла — положительное число, которое показывает, сколько раз градус и его части укладываются в данном углу.

Есть еще две возможные меры угла: минуты и секунды. Они позволяют выполнять более точные расчеты, особенно, когда величина не является целым обозначением градуса.

Минута — 1/60 часть градуса. Обозначается — ´.

Секунда — 1/60 часть минуты. Обозначается — ´´.

Градус состоит из 3600 секунд, то есть: 1° = 60′ = 3600′.

Как происходит измерение угла: сначала измеряются стороны угла, а после его внутренняя область. Всегда нужно считать количество уложенных углов, так как они предопределяют меру измеряемого угла.

Когда луч делит угол на два или более углов, градусная мера всего угла равна сумме градусных мер этих углов.

На рисунке изображен угол АОВ, он состоит из углов АОС, СОD и DОВ. Можно записать так: ∠ A O B = ∠ A O C + ∠ D O B = 45° + 30° + 60° = 135 °.

Угол называется прямым, если он равен 90°, а острым, если он меньше 90°, тупым, если он больше 90°, но меньше 180°. Развернутый угол имеет 180°.

Равные углы имеют равную градусную меру.

Обозначение углов на чертеже

Чертеж помогает решать задачки по геометрии в разы быстрее. Чтобы наглядно изображать дуги, углы и прочие фигурки, придумали даже отдельное направление — геометрический чертеж.

Задачи с углами могут быть разными и не всегда есть возможность правильно изобразить и отметить угол. Вот, что важно запомнить при обозначении лучей и углов:

• Равные углы обозначают одинаковым количеством дуг.
• Неравные углы обозначают разным количеством дуг, чтобы они отличались между собой.
• Для обозначения на чертеже более трех углов используем разные виды дуг: волнистые, зубчатые.

На чертеже отмечены острые, равные и неравные углы.

Обозначать углы можно разными цветами. Главное, чтобы было просто и броско. При этом необязательно отмечать все-все углы — достаточно только тех, которые нам нужны для решения задачки.

Вникать во все тонкости математической вселенной комфортнее с внимательным наставником. Наши учителя объяснят сложную тему, ответят на неловкие вопросы и вдохновят ребенка учиться. А красочная платформа с увлекательными заданиями поможет заниматься современно и в удовольствие. Запишите ребенка на бесплатный пробный урок в онлайн-школу Skysmart и попробуйте сами!

определение угла, измерение углов, обозначения и примеры

Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.

Определение угла

Определение 1

Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения.

Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости.

Определение 2

Дана прямая a на плоскости. На ней обозначим некоторую точку O. Прямая разделена точкой на две части, каждая из которых имеет название луч, а точка O – начало луча.

Иначе говоря, луч или полупрямая – это часть прямой, состоящая из точек заданной прямой, расположенных на одной стороне относительно начальной точки, то есть точки O.

Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.

Перейдем к понятию определения угла.

Определение 3

Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон.

Имеет место случай, когда стороны угла могут выступать в роли прямой линии.

Определение 4

Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым.

На рисунке ниже изображен развернутый угол.

Точка на прямой – это и есть вершина угла. Чаще всего имеет место ее обозначение точкой O.

Угол в математике обозначается знаком «∠ ». Когда стороны угла обозначают малыми латинскими, то для правильного определения угла записываются подряд буквы соответственно сторонам. Если две стороны имеют обозначение k и h, то угол обозначается как ∠kh или ∠hk .

Когда идет обозначение большими буквами, то соответственно стороны угла имеют названия OA и OB. В таком случае угол имеет название из трех букв латинского алфавита, записанные подряд, в центре с вершиной — ∠AOB и ∠BOA . Существует обозначение в виде цифр, когда углы не имеют названий или буквенных обозначений. Ниже приведен рисунок, где разными способами обозначаются углы.

Угол делит плоскость на две части. В случае, если угол не развернутый, тогда одна часть плоскости имеет название внутренняя область угла, другая – внешняя область угла. Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.

При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.

Внутренняя область угла – элемент, служащий для второго определения угла.

Определение 5

Углом называют геометрическую фигуру, состоящая из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла.

Данное определение является более строгим, чем предыдущее, так как имеет больше условий. Оба определения не желательно рассматривать отдельно, потому как угол – это геометрическая фигура, преобразованная при помощи двух лучей, выходящих из одной точки. Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью.

Определение смежных и вертикальных углов

Определение 6

Два угла называют смежными, если имеется общая сторона, а две другие являются дополнительными полупрямыми или образуют развернутый угол.

На рисунке видно, что смежные углы дополняют друг друга, так как являются продолжением один другого.

Определение 7

Два угла называют вертикальными, если стороны одного являются дополнительными полупрямыми другого или являются продолжениями сторон другого. На рисунке ниже показано изображение вертикальных углов.

При пересечении прямых получается 4 пары смежных и 2 пары вертикальных углов. Ниже показано на рисунке.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

Сравнение углов

Статья показывает определения равных и неравных углов. Разберем какой угол считается большим, какой меньшим и другие свойства угла. Две фигуры считаются равными, если при наложении они полностью совпадают. Такое же свойство применимо для сравнения углов.

Даны два угла. Необходимо прийти к выводу, равные эти углы или нет.

Известно, что имеет место наложение вершин двух углов и стороны первого угла с любой другой стороной второго. То есть при полном совпадении при наложении углов стороны заданных углов совместятся полностью, углы равные.

Может быть так, что при наложении стороны могут не совместиться, то углы неравные, меньший из которых состоит из другого, а больший имеет в своем составе полный другой угол. Ниже изображены неравные углы, не совмещенные при наложении.

Развернутые углы являются равными.

Измерение углов

Измерение углов начинается с измерения стороны измеряемого угла и его внутренней области, заполняя которую единичными углами, прикладывают друг к другу. Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла.

Единица измерения угла может быть выражена любым измеряемым углом. Имеются общепринятые единицы измерения, которые применяют в науке и технике. Они специализируются на других названиях.

Чаще всего используют понятие градус.

Определение 8

Один градус называют углом, который имеет одну сто восьмидесятую часть развернутого угла.

Стандартное обозначение градуса идет при помощи «°», тогда один градус – 1° . Следовательно, развернутый угол состоит из 180 таких углов, состоящих из одного градуса.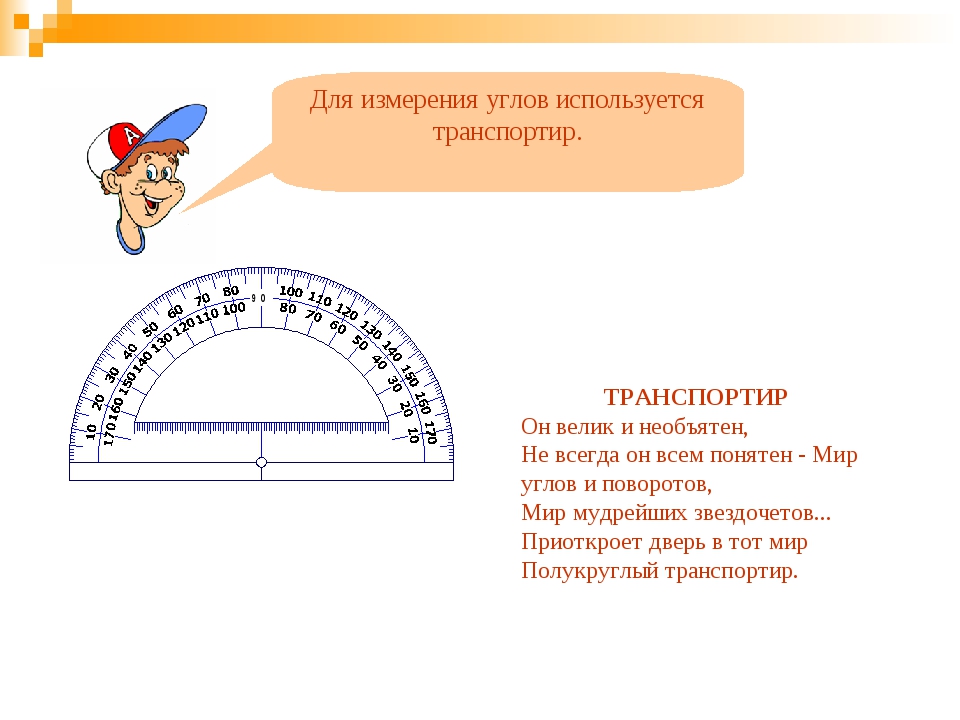 Все имеющиеся углы плотно уложены друг к другу и стороны предыдущего совмещены с последующим.

Известно, что количество положенных градусов в угле, это и есть та самая мера угла. Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина.

Для точности определения измерения углов используются минуты и секунды. Их применяют, когда величина угла не является целым обозначением градуса. Такие части градуса позволяют выполнять более точные расчеты .

Определение 9

Минутой называют одну шестидесятую часть градуса.

Определение 10

Секундой называют одну шестидесятую часть минуты.

Градус содержит 3600 секунд. Минуты обозначают «’», а секунды «»». Имеет место обозначение:

1°=60’=3600», 1’=(160)°, 1’=60», 1»=(160)’=(13600)° ,

а обозначение угла 17 градусов 3 минут и 59 секунд имеет вид 17°3’59» .

Определение 11

Градусная мера угла –это число, показывающее количество укладываний градуса в заданном угле.

Приведем пример обозначения градусной меры угла равного 17°3’59» . Запись имеет еще один вид 17+360+593600=172393600.

Для точного измерения углов используют такой измерительный прибор, как транспортир. При обозначении угла ∠AOB и его градусной мере в 110 градусов применяют более удобную запись ∠AOB=110° , которая читается «Угол АОВ равен 110градусам».

В геометрии используется мера угла из интервала (0,180], а в тригонометрии произвольная градусная мера имеет название углов поворота. Значение углов всегда выражается действительным числом. Прямой угол – это угол, имеющий 90 градусов. Острый угол – угол, который меньше 90 градусов, а тупой – больше.

Острый угол измеряется в интервале (0,90), а тупой – (90,180). Ниже наглядно изображены три вида углов.

Любая градусная мера любого угла имеет одинаковое значение. Больший угол соответственно имеет большую градусную меру, чем меньший. Градусная мера одного угла – это сумма всех имеющихся градусных мер внутренних углов. Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так:∠AOB=∠AOC+∠DOB=45°+30°+60°=135° .

Исходя из этого, можно сделать вывод, что сумма всех смежных углов равна 180 градусам, потому что они все и составляют развернутый угол.

Отсюда следует, что любые вертикальные углы равны. Если рассмотреть это на примере, мы получим, что угол АОВ и СОD – вертикальные (на чертеже), тогда пары углов АОВ и ВОС, СОD и ВОС считают смежными. В таком случает равенство∠AOB+∠BOC=180° вместе с ∠COD+∠BOC=180° считаются однозначно верными. Отсюда имеем, что ∠AOB=∠COD . Ниже приводится пример изображения и обозначения вертикальных улов.

Кроме градусов, минут и секунд используется еще одна единица измерения. Она называется радианом. Чаще всего ее можно встретить в тригонометрии при обозначении углов многоугольников. Что же называют радианом.

Определение 12

Углом в один радиан называют центральный угол, который имеет длину радиуса окружности равную длине дуги.

На рисунке радиан изображается в виде окружности, где имеется центр, обозначенный точкой , с двумя точками на окружности, соединенными и преобразованными в радиусы ОА и ОВ. По определению данный треугольник AOB является равносторонним, значит длина дуги AB равна длинам радиусов ОВ и ОА.

Обозначение угла принимается за «рад». То есть запись в 5 радиан сокращенно обозначается как 5 рад. Иногда можно встретить обозначение, имеющее название пи. Радианы не имеют зависимости от длины заданной окружности, так как фигуры имеют некое ограничение при помощи угла и его дугой с центром, находящимся в вершине заданного угла. Они считаются подобными.

Радианы имеют такой же смысл, как и градусы, только разница в их величине. Чтобы это определить, необходимо вычисленную длину дуги центрального угла поделить на длину ее радиуса.

На практике используют перевод градусов в радианы и радианы в градусы для более удобного решения задач. Указанная статья имеет информацию о связи градусной меры с радианной, где можно подробно изучить переводы из градусной в радианную и обратно.

Обозначение углов на чертеже

Для наглядного и удобного изображения дуг, углов используют чертежи. Не всегда можно правильно изобразить и отметить тот или иной угол, дугу или название. Равные углы имеют обозначение в виде одинакового количества дуг, а неравные в виде разного. На чертеже изображено правильное обозначение острых, равных и неравных углов.

Когда необходимо отметить более 3 углов, используются специальные обозначения дуг, например, волнистые или зубчатые. Это не имеет столь важное значение. Ниже приведен рисунок, где показано их обозначение.

Обозначение углов должны быть простыми, чтобы не мешали другим значениям. При решении задачи рекомендовано выделять только необходимые для решения углы, чтобы не загромождать весь чертеж. Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.

Как найти меру угла

Два луча с одной и той же конечной точкой создают угол. Точка, в которой они пересекаются, называется вершиной. Угол образует часть воображаемого круга. А поскольку круги измеряют 360 градусов, вы можете найти угол, образованный лучами. Вот несколько вещей, которые вы должны знать о том, как найти величину угла.

Четыре типа углов

Есть четыре типа углов. Знание разницы поможет вам оценить размер угла.Вот четыре типа углов и размеров, которые помогут вам классифицировать каждый из них.

Прямой угол (180 градусов)

Острый угол (менее 90 градусов)

Прямой угол (90 градусов)

Тупой угол (более 90 градусов, но менее 180 градусов)

Использование транспортира

Лучший способ измерить угол — использовать транспортир. Для этого вы начнете с выстраивания одного луча вдоль 0-градусной линии транспортира. Затем совместите вершину с серединой транспортира.Следуйте по второму лучу, чтобы определить угол с точностью до градуса.

Углы в треугольниках

Треугольники получили свое название от трех углов, которыми они обладают. Эти три угла в сумме должны составлять 180 градусов. Часто у вас есть измерения двух углов. Однако вам придется вычислить размер третьего угла. Используемое уравнение:

угол A + угол B + угол C = 180 градусов.

Например, у вас есть следующий треугольник.Что такое измерение угла C?

Если вы подставите эти числа в уравнение, вы получите следующее уравнение:

Уголки в четырехугольнике

Квадраты и прямоугольники имеют четыре прямых угла. Если сложить углы, получится 90 + 90 + 90 + 90 = 360. Четырехугольник также имеет четыре угла. Следовательно, углы формы составляют в сумме 360 градусов, даже если нет прямых углов. Чтобы определить недостающий угол четырехугольника, вы можете использовать следующее уравнение:

угол A + угол B + угол C + угол D = 360 градусов.

Посмотрите следующий пример. Можете ли вы определить недостающий угол в этом четырехугольнике?

Чтобы найти недостающий угол, подставьте значения угла в уравнение:

Работаете ли вы с лучом, треугольником или четырехугольником, существуют методы, которые можно использовать для обнаружения недостающего измерения угла. Если вам интересно, как найти угол на луче, треугольнике или четырехугольнике, попробуйте использовать транспортир или уравнения, которые мы обсуждали.Они должны работать и помогать вам немного облегчить жизнь!

О Джейми Гудвине

Джейми окончил Университет Бригама Янга в Айдахо по специальности «Английское образование». Она провела несколько лет, обучая и обучая учеников начальной, средней школы и колледжа. В настоящее время она работает писателем по контракту и разработчиком учебных программ для онлайн-курсов. В свободное время она любит бегать и проводить время со своими мальчиками!

Измерьте и классифицируйте угол (геометрия, точки, линии, плоскости и углы) — Mathplanet

Линия, имеющая одну определенную конечную точку, называется лучом и продолжается бесконечно в одном направлении.Луч назван в честь конечной точки и другой точки на луче, например.

$$ \ overset {\ rightarrow} {AB} $$

Угол, который образуется между двумя лучами с одинаковой конечной точкой, измеряется в градусах. Точка называется вершиной

.

Вершина записывается как

$$ \ Измеренный угол CAB $$

В алгебре мы использовали координатную плоскость для построения графиков и решения уравнений. Вы можете наносить линии, отрезки, лучи и углы на координатную плоскость.

В координатной плоскости выше у нас есть два луча

$$ \ overset {\ rightarrow} {BA} \: \: и \: \: \ overset {\ rightarrow} {BD} $$

образуют угол с вершиной в точке B.

Вы можете использовать координатную плоскость для измерения длины отрезка. Точка B находится в (-2, -2) и C (1,2). Расстояние между двумя точками составляет 1 — (-2) = 3 единицы.

Углы могут быть прямыми, прямыми, острыми или тупыми.

Угол — это часть окружности, в которой весь круг равен 360 °.Прямой угол равен половине круга и равен 180 °, тогда как прямой угол равен четверти круга и равен 90 °.

Вы измеряете угол с помощью транспортира.

Два угла с одинаковой мерой называются конгруэнтными углами. Конгруэнтные углы обозначены как

.

$$ \ угол A \ конг \ угол B $$

Или может быть показан дугой на рисунке, чтобы указать, какие углы совпадают.

Два угла, общая длина которых составляет 180 °, называются дополнительными e.{\ circ} $$

---

Видеоурок

Измерьте размер уголка

Углы измерения

| Важность | Разные системы

18 ноября 2020

Время чтения: 4 минуты

Линии и углы — первые понятия геометрии, которые изучает студент. Линия — это набор точек, а угол образуется при пересечении двух лучей. Луч — это линия, которая бесконечно проходит в одном направлении.

Когда два луча исходят из общей точки, наклон одного луча к другому называется углом.

Также читайте:

---

Геометрия создает пространство для учащихся рисовать и изучать 2D и 3D формы. Но с чего это начинается? Для измерения угла могут потребоваться простые математические уравнения или более сложная геометрия.

Для измерения угла обычно нужен транспортир.Загрузите PDF-файл ниже, чтобы узнать, почему важны углы и разные системы измерения угла.

📥

Как найти угол?

Загрузить

Почему важны углы?

Углы используются в самых разных целях: от забавных, как в игре в карром, до более сложных, таких как движение планет.

Строительство, архитектура, спорт, инженерия, искусство, танцы и т. Д. Используют понятие углов. Помимо этого, ученые и астрономы полагаются на углы, под которыми небесные тела делают, чтобы изучить их движение и прийти к конкретным выводам.

При измерении вы будете иметь дело с вершиной угла, где две линии встречаются, образуя угол. Углы измеряются в градусах. Измерение углов может помочь нам лучше подготовиться к работе с числами и измерениями, а также к использованию наших визуальных способностей.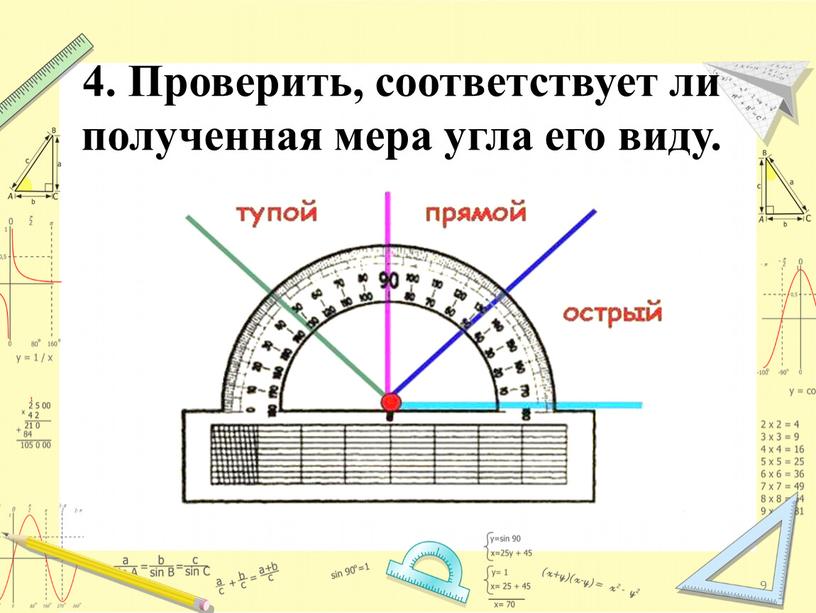

---

Примеры вопросов и ответов

Давайте рассмотрим несколько примеров вопросов и ответов о том, как найти меру угла —

Q.1 Какова сумма внутренних углов треугольника?

Ответ — Сумма внутренних углов треугольника составляет 180 градусов.

Q.2 Два внутренних угла треугольника составляют 50 и 45. Какая наибольшая мера любого из его внешних углов?

Ответ — Внутренние углы треугольника должны иметь меры, сумма которых равна 180, поэтому размер третьего угла должен быть

.

180 — (50 + 45) = 85

Согласно теореме о внешнем угле треугольника, внешний угол треугольника измеряет сумму его удаленных внутренних углов; поэтому, чтобы получить наибольшую меру любого внешнего угла, мы добавляем две наибольшие меры внутреннего угла:

50 + 85 = 135

Q.3 Два угла являются дополнительными и имеют соотношение 1: 4. Каков размер меньшего угла?

Ответ — Так как углы дополнительные, их сумма составляет 180 градусов. Поскольку они находятся в соотношении 1: 4, можно записать следующее выражение:

х + 4х = 180

5x = 180

х = 36

Q.4 В данном треугольнике углы находятся в соотношении 1: 3: 5. Какого размера средний угол?

Ответ — Сумма углов треугольника 180

, и, учитывая, что углы находятся в соотношении 1: 3: 5, пусть мера наименьшего угла будет

x, то можно записать следующее выражение:

х + 3х + 5х = 180

9x = 180

х = 20

Если наименьший угол равен 20 градусам, то, учитывая, что средний угол находится в соотношении 1: 3, средний угол будет в 3 раза больше, или 60 градусов.

Q.5 Сумма двух внутренних углов треугольника составляет 64 градуса. Какова мера другого угла?

Ответ — Сумма трех углов треугольника составляет 180 градусов.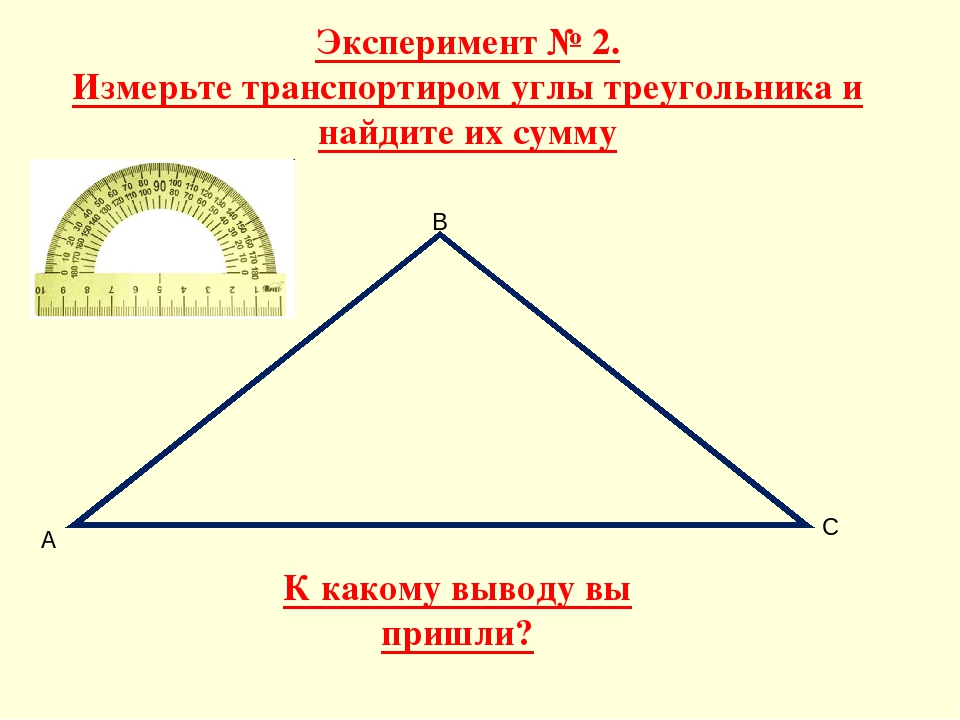 Вычтите 64 градуса, чтобы определить третий угол.

180–64 = 116

---

Знаете ли вы стандартные системы измерения углов?

Вот различные стандартные системы, используемые для измерения углов. Мы упростили их для вас, чтобы помочь вашим ученикам

1.Степень

Градус — это измерение плоского угла, составляющего 1/360 полного оборота. Обычно обозначается как °.

Почему 360 ° считается углом для одного полного поворота?

Считается, что вавилоняне изобрели градус и всегда считали по основанию 60. Вот где родились первые идеи 360. Его считали из-за того, что он легко делится на множество чисел. Например, 360 делится на все числа от 1 до 10, кроме 7.Наука также подтверждает, что Земле требуется около 365 дней, чтобы совершить один оборот вокруг Солнца. В большинстве основных календарей в году около 360 дней.

градусов измеряются с помощью транспортира и являются одним из наиболее распространенных методов измерения углов.

2. Radian

Радианная мера угла определяется как отношение длины дуги, которую угол образует окружность, к длине радиуса той же окружности.

Это соотношение даст вам величину угла в радианах.

В радианах нет единицы. Почему? Поскольку это соотношение двух длин, следовательно, единицы отменяются.

3. Революция

Оборот считается самой простой и естественной единицей измерения геометрических углов. Революции помогают учащимся понять более глубокое значение углов. Это потому, что угол — это, по сути, подразделение круга, а не сумма нескольких градусов.Например, ученикам легче понять, что «прямой угол составляет четверть круга», чем «прямой угол равен 90 °

.

Знакомство учащихся с поворотами и градусами поможет им лучше понять концепцию углов. Вот иллюстрация, с помощью которой вы можете пояснить разницу между тремя системами измерения углов

.

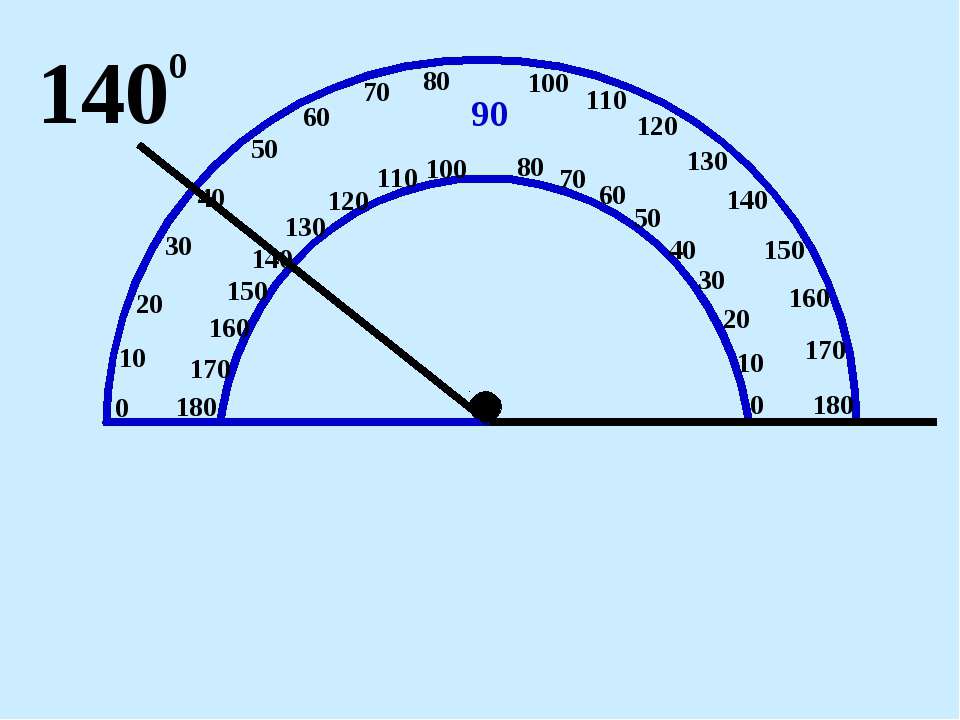
Помимо стандартных систем, хорошо на раннем этапе у учащегося сформировать представление о том, что единицей измерения угла является угол.Его не «нужно» измерять в градусах. Они могут создать свою собственную систему измерения и использовать ее для измерения углов.

Учащимся легче развить чувство измерения угла с помощью клина, а не транспортира. Транспортир с бумажным клином можно сделать, сложив круг пополам четыре раза, пока не будут сформированы 16 клиньев (или секторов). Если бумага прозрачная, то ее можно положить на угол многоугольника или угловой луч. Количество клиньев можно подсчитать.

Поощряйте своих учеников открывать новые методы измерения углов, и кто знает, в ближайшие годы их метод может стать традиционным.

---

Сводка

Суммируем:

• Два луча с одинаковой конечной точкой образуют угол. Углы можно найти в различных объектах вокруг нас, будь то ножницы, хоккейная клюшка или стул.
• Точка, в которой они пересекаются, называется вершиной, которая является общей конечной точкой лучей / отрезков линии.При названии угла вершина всегда находится в центре.
• Измерение углов может помочь улучшить пространственное понимание и взаимосвязь между числами и измерениями, они не только полезны в учебе, но и изучение углов помогает нам понимать и использовать вещи вокруг нас.

Мы надеемся, что эта статья о том, как найти меру угла, показалась вам интересной и информативной. Не стесняйтесь поделиться этой статьей. Убедитесь, что вы регулярно пересматриваете эти концепции, пока они не будут полностью поняты, поскольку они являются базовыми и основополагающими.Регулярно посвящайте от 30 до 45 минут изучению, пониманию и практике концепций. Вы можете узнать больше об углах у нас, запишитесь на бесплатное занятие.

---

О компании Cuemath

Cuemath, удобная для учащихся платформа математики и кодирования, проводит регулярные онлайн-классы для преподавателей и развития навыков, а их приложение Mental Math для iOS и Android представляет собой универсальное решение для детей, развивающее несколько навыков. Ознакомьтесь со структурой Cuemath Fee и подпишитесь на бесплатную пробную версию.

---

Часто задаваемые вопросы (FAQ)

Как найти угол в окружности?

Окружность имеет в сумме 360 градусов от центра до центра, если центральный угол, определяющий сектор, имеет угловую меру 60 градусов, тогда сектор занимает 60/360 или 1/6 градусов от всех наоборот. В этом случае сектор составляет 1/6 площади всего круга.

Как найти размер дуги с вписанным углом?

Вписанный угол имеет вершину на окружности, а стороны угла лежат на двух хордах окружности.Размер вписанного угла составляет половину дуги, которую две стороны вырезают из круга.

Как найти меру внутреннего угла?

Вписанный угол имеет вершину на окружности, а стороны угла лежат на двух хордах окружности. Размер вписанного угла составляет половину дуги, которую две стороны вырезают из круга.

Что такое градусная мера и как найти градусную меру угла?

В этой системе угол измеряется в градусах, минутах и ​​секундах.Степень обозначается как º.
1 прямой угол = 90 градусов или 90 градусов.

---

Внешние ссылки

Играть в угловые игры — SplashLearn

Построение углов — Math Only Math

Измерение углов

Измерение углов

Понятие угла

Понятие угла — одно из важнейших понятий в геометрии. Понятия равенства, суммы и разности углов важны и используются во всей геометрии, но предмет тригонометрии основан на измерении углов .

Есть две обычно используемые единицы измерения углов. Более знакомая единица измерения — это градусы. Круг делится на 360 равных градусов, так что прямой угол равен 90 °. Пока мы будем рассматривать только углы от 0 ° до 360 °, но позже, в разделе о тригонометрических функциях, мы будем рассматривать углы больше 360 ° и отрицательные углы. Градусы можно разделить на минуты и секунды, но это деление не так универсально, как раньше.Каждый градус делится на 60 равных частей, называемых минутами. Итак, семь с половиной градусов можно назвать 7 градусами и 30 минутами, записанными как 7 ° 30 ‘. Каждая минута далее делится на 60 равных частей, называемых секунд, и, например, 2 градуса 5 минут 30 секунд записывается как 2 ° 5 ’30 «. Деление градусов на минуты и угловые секунды аналогично делению на часы в минуты и секунды.

Части градуса теперь обычно обозначаются десятичной дробью.Например, семь с половиной градусов теперь обычно пишут как 7,5 & deg.

Когда один угол нарисован на плоскости xy для анализа, мы нарисуем его в стандартной позиции с вершиной в начале координат (0,0), одна сторона угла вдоль x ось, а другая сторона выше оси x .

Радианы

Другое распространенное измерение углов — радианы.Для этого измерения рассмотрим единичный круг (круг радиуса 1), центр которого является вершиной рассматриваемого угла. Затем угол отсекает дугу окружности, и длина этой дуги является мерой угла в радианах. Легко переходить между градусами и радианами. Окружность всего круга равна 2 π , следовательно, 360 ° равняется 2 π радиан. Следовательно, 1 ° равняется π /180 радиан и 1 радиан равен 180/ π градусов Большинство калькуляторов можно настроить на использование углов, измеряемых в градусах или радианах.Убедитесь, что вы знаете, в каком режиме работает ваш калькулятор.

Краткая заметка по истории радианов

Хотя слово «радиан» было придумано Томасом Мьюиром и / или Джеймсом Томпсоном около 1870 года, математики долгое время измеряли углы таким способом. Например, Леонард Эйлер (1707–1783) в своей работе Elements of Algebra явно сказал, что углы следует измерять по длине дуги, отрезанной в единичной окружности. Это было необходимо, чтобы дать его знаменитую формулу, включающую комплексные числа, которая связывает функции знака и косинуса с экспоненциальной функцией. e ^iθ = cos θ + i sin θ

где θ — это то, что позже было названо измерением угла в радианах. К сожалению, объяснение этой формулы выходит далеко за рамки этих заметок. Но для получения дополнительной информации о комплексных числах см. Мой Краткий курс комплексных чисел.

Радианы и длина дуги

Альтернативное определение радианов иногда дается в виде отношения. Вместо того, чтобы брать единичную окружность с центром в вершине угла θ , возьмите любую окружность с центром в вершине угла. Тогда радианная мера угла — это отношение длины вытянутой дуги к радиусу r окружности. Например, если длина дуги равна 3, а радиус круга равен 2, тогда мера в радианах равна 1.5.

Причина, по которой это определение работает, заключается в том, что длина вытянутой дуги пропорциональна радиусу круга. В частности, определение в терминах отношения дает ту же цифру, что и приведенная выше с использованием единичного круга. Однако это альтернативное определение более полезно, поскольку вы можете использовать его для соотнесения длин дуг с углами. Длина дуги равна радиусу r , умноженному на угол θ , где угол измеряется в радианах.

Например, дуга θ = 0,3 радиана в окружности радиуса r = 4 имеет длину 0,3 умноженную на 4, то есть 1,2.

Радианы и площадь сектора

Сектор круга — это часть круга, ограниченная двумя радиусами и дугой круга, соединяющей их концы. Площадь этого сектора легко вычислить по радиусу r окружности и углу θ между радиусами, если он измеряется в радианах.Так как площадь всего круга составляет πr ² , а сектор относится к всей окружности, так как угол θ равен 2 π , поэтому

Общие углы

Ниже приведена таблица общих углов как при измерении в градусах, так и при измерении радиан. Обратите внимание, что измерение в радианах дано в терминах π . Его, конечно, можно было бы дать десятичной дроби, но радианы часто появляются с коэффициентом π .

Уголок	градусов	Радианы
	90 °	π /2
	60 °	π /3
	45 °	π /4
	30 °	π /6

Упражнения

Эдвин С.Кроули написал книгу « Тысяча упражнений в плоской и сферической тригонометрии», Университет Пенсильвании, Филадельфия, 1914. Задачи этого короткого курса взяты из этого текста (но не все 1000 из них!). пять знаков точности, поэтому студентам пришлось потрудиться, чтобы решить их, и они использовали таблицы логарифмов, чтобы помочь в умножении и делении. Студенты должны были уметь пользоваться таблицей синус-косинусов, таблицей касательных, таблицей логарифмов, таблицей log-sin-cos и таблицей log-tan.Теперь мы можем пользоваться калькуляторами! Это означает, что вы можете сосредоточиться на концепциях, а не на трудоемких вычислениях.

Кроули использовал не десятичные дроби для дробей градуса, а минуты и секунды.

Каждый комплекс упражнений включает в себя, во-первых, формулировку упражнений, во-вторых, некоторые подсказки для решения упражнений, а в-третьих, ответы на упражнения.

1. Выразите следующие углы в радианах.
(а). 12 градусов, 28 минут, то есть 12 ° 28 ‘.
(б). 36 ° 12 ‘.

2. Сократите следующие числа радианов до градусов, минут и секунд.
(а). 0,47623.
(б). 0,25412.

3. Учитывая угол a и радиус r, , чтобы найти длину проходящей дуги.
(а). a = 0 ° 17 ’48 дюймов, r = 6,2935.
(б). a = 121 ° 6 ’18 дюймов, r = 0,2163.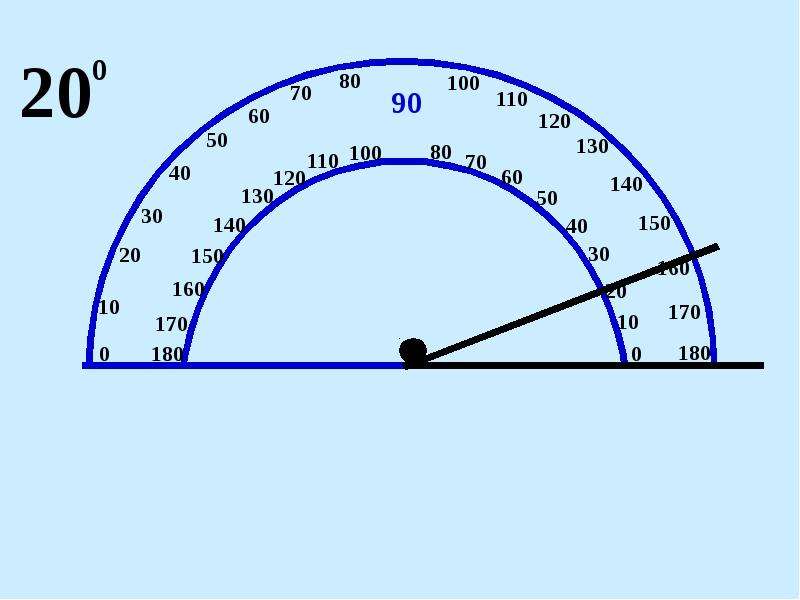

4. Учитывая длину дуги l и радиус r, , чтобы найти угол, стянутый в центре.
(а). l = 0,16296, r = 12,587.
(б). l = 1,3672, r = 1,2978.

5. Зная длину дуги l и угол a , который она проходит в центре, найти радиус.
(а). a = 0 ° 44 ’30 дюймов, l = 0,032592.
(б). a = 60 ° 21 ‘6 дюймов, l = 0,4572.

6. Найдите длину с точностью до дюйма дуги окружности 11 градусов 48,3 минуты, если радиус составляет 3200 футов.

7. Кривая железной дороги образует дугу окружности 9 градусов 36,7 минут, радиус до центральной линии пути составляет 2100 футов. Если калибр 5 футов, найдите разницу в длине двух рельсов с точностью до полудюйма.

9. На сколько можно изменить широту, идя на север на одну милю, если предположить, что Земля представляет собой сферу радиусом 3956 миль?

10. Вычислите длину в футах одной угловой минуты на большом круге Земли. Какова длина дуги в одну секунду?

14. На окружности радиусом 5,782 метра длина дуги составляет 1,742 метра. Какой угол он образует в центре?

23. Воздушный шар, известный как 50 футов в диаметре, сужается к глазу под углом 8 1/2 минут.Как далеко это?

Подсказки

1. Чтобы преобразовать градусы в радианы, сначала преобразуйте количество градусов, минут и секунд в десятичную форму. Разделите количество минут на 60 и прибавьте к количеству градусов. Так, например, 12 ° 28 ‘равно 12 + 28/60, что равно 12,467 °. Затем умножьте на π и разделите на 180, чтобы получить угол в радианах.

2. И наоборот, чтобы преобразовать радианы в градусы, разделите на π и умножьте на 180.Таким образом, 0,47623, деленное на π и умноженное на 180, дает 27,286 °. Вы можете преобразовать доли градуса в минуты и секунды следующим образом.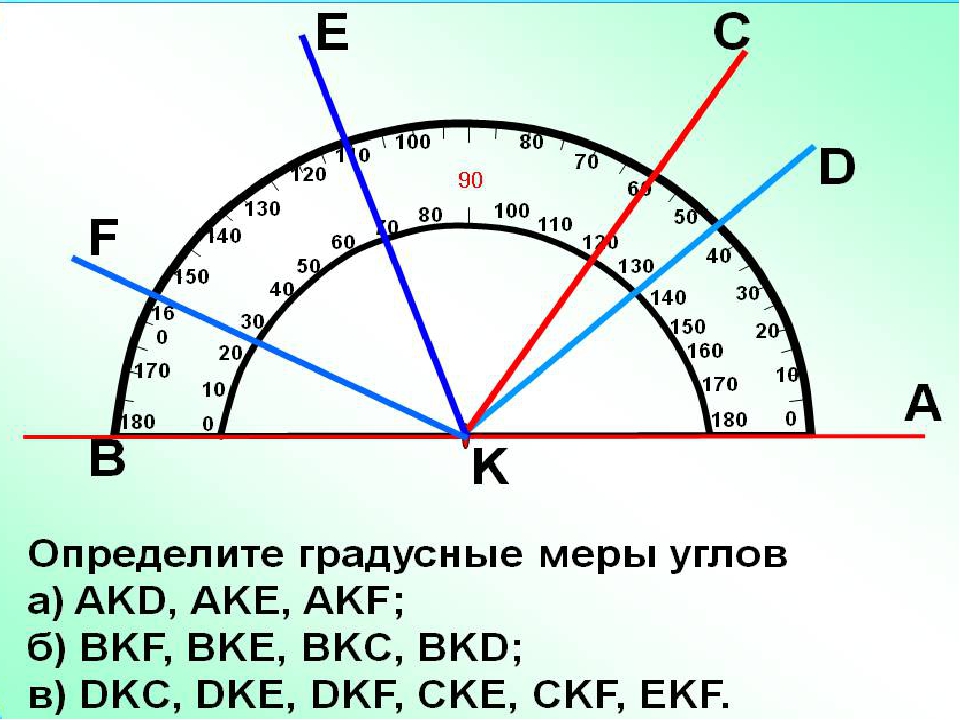 Умножьте дробь на 60, чтобы получить количество минут. Здесь 0,286 умножить на 60 равно 17,16, поэтому угол можно записать как 27 ° 17,16 ‘. Затем возьмите любую оставшуюся долю минуты и снова умножьте на 60, чтобы получить количество секунд. Здесь 0,16 умножить на 60 равно примерно 10, поэтому угол также можно записать как 27 ° 17 ’10 дюймов.

3. Чтобы найти длину дуги, сначала преобразуйте угол в радианы. Для 3 (a) 0 ° 17’48 «составляет 0,0051778 радиана. Затем умножьте его на радиус, чтобы найти длину дуги.

4. Чтобы найти угол, разделите его на радиус. Это дает вам угол в радианах. Их можно преобразовать в градусы, чтобы получить ответы Кроули.

5. Как упоминалось выше, радиан умноженный на радиус = длина дуги, поэтому, используя буквы для этой задачи, ar = l, , но a необходимо сначала преобразовать из градусного измерения в радиан. .Итак, чтобы найти радиус r, сначала преобразует угол a в радианы, а затем разделит его на длину l дуги.

6. Длина дуги равна радиусу, умноженному на угол в радианах.

7. Помогает нарисовать фигуру. Радиус внешнего рельса равен 2102,5, а радиус внутреннего рельса — 2097,5.

9. У вас есть круг радиусом 3956 миль и дуга этого круга длиной 1 милю.Какой угол в градусах? (Средний радиус Земли был известен довольно точно в 1914 году. Посмотрим, сможете ли вы узнать, каким, по мнению Эратосфена, был радиус Земли, еще в III веке до н. Э.)

10. Угловая минута равна 1/60 градуса. Преобразовать в радианы. Радиус — 3956. Какова длина дуги?

14. Поскольку длина дуги равна радиусу, умноженному на угол в радианах, отсюда следует, что угол в радианах равен длине дуги, деленной на радиус.Радианы легко преобразовать в градусы.

23. Представьте, что диаметр воздушного шара является частью дуги окружности с вами в центре.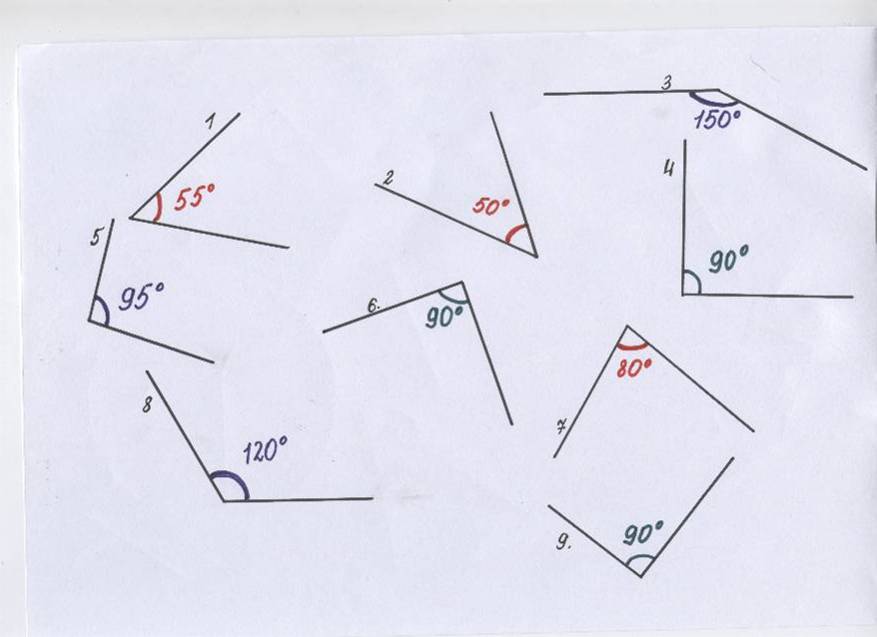 (Это не совсем часть дуги, но довольно близко). Длина дуги составляет 50 футов. Вы знаете угол, так каков радиус этого круга?

Ответы

1. (а). 0,2176. (б). 0,6318.

2. (а). 27 ° 17 ’10 «. (B). 14,56 ° = 14 ° 33,6′ = 14 ° 33’36».

3. (а). 0,03259 (б). 2,1137 умножить на 0,2163 равно 0,4572.

4. (а). 0,16296 / 12,587 = 0,012947 радиан = 0 ° 44 ’30 дюймов.
(б). 1,3672 / 1,2978 = 1,0535 радианы = 60,360 ° = 60 ° 21,6 ‘= 60 ° 21’ 35 «.

5. (а). л / год = 0,032592 / 0,01294 = 2,518.
(б). л / год = 0,4572 / 1,0533 = 0,4340.

6. ra = (3200 ‘) (0.20604) = 659,31 ‘= 659’ 4 дюйма.

7. Угол a = 0,16776 радиана. Разница в длине составляет 2102,5 a -1997,5 a , что составляет 5 a. Таким образом, ответ составляет 0,84 фута, что с точностью до дюйма составляет 10 дюймов.

9. Угол = 1/3956 = 0,0002528 радиан = 0,01448 ° = 0,8690 ‘= 52,14 дюйма.

10. Одна минута = 0,0002909 радиан. 1.15075 миль = 6076 футов.Следовательно, одна секунда будет соответствовать 101,3 фута.

14. a = л / об = 1,742 / 5,782 = 0,3013 радиан = 17,26 ° = 17 ° 16 ‘.

23. Угол a равен 8,5 ‘, что составляет 0,00247 радиана. Таким образом, радиус равен r = л / год = 50 / 0,00247 = 20222 ‘= 3,83 мили, почти четыре мили.

Насчет цифр точности.

Кроули старается давать свои ответы примерно с той же точностью, что и данные в вопросах.Это важно, особенно сейчас, когда у нас есть калькуляторы. Например, в задаче 1 точка отсчета равна 12 ° 28 ‘, что соответствует примерно четырем знакам точности, поэтому ответ 0,2176 также должен быть дан только с точностью до четырех знаков. (Обратите внимание, что ведущие нули не учитываются при вычислении цифр точности. ) Ответ 0,21758438 предполагает восемь цифр точности, и это может ввести в заблуждение, поскольку данная информация не была такой точной.

Другой пример см. В задаче 3 (a). Данные 0 ° 17’48 «и 6.2935 с точностью до 4 и 5 знаков соответственно. Следовательно, ответ должен быть дан только с точностью до 4 цифр, так как ответ не может быть более точным, чем наименее точные данные. Таким образом, ответ, который может дать калькулятор, а именно 0,032586547, следует округлить до четырех цифр (не включая ведущие нули) до 0,03259.

Хотя окончательные ответы должны быть выражены с соответствующим числом цифр точности, вы все равно должны сохранять все цифры для промежуточных вычислений.

Как использовать транспортир для измерения углов

Транспортир — это инструмент для измерения углов, обычно в градусах. ^[1] Они бывают полукруглых версий, как показано выше, или полукруглых версий, хотя полукруг является наиболее распространенным типом.

Полукруглый транспортир измеряет 180 °, а линейка полного круга может измерять 360 °. Часто транспортиры четкие, поэтому вы можете видеть свои линии и формы под инструментом во время измерения, и они имеют ряд делений вдоль внешних краев для измерения углов.

Как измерить угол с помощью транспортира

Вы можете использовать транспортир, чтобы измерить угол за несколько простых шагов. Сначала определите вершину или центральную точку угла, затем поместите исходную / центральную точку транспортира над вершиной.Затем совместите нижний край транспортира с одним из краев, или лучей угла, и, наконец, прочтите значение угла.

Шаг 1. Найдите вершину или центральную точку угла

Вершиной угла считается точка пересечения двух лучей (линий). ^[2] Найдите две линии и посмотрите, где они встречаются. Если две линии угла не соприкасаются, используйте прямую часть транспортира, чтобы удлинить линии, пока они не встретятся, чтобы найти вершину.

Шаг 2. Поместите начало координатной точки над вершиной

Найдите начало координат на транспортире, которое находится рядом с прямым краем транспортира и в центре. Обычно есть отверстие или круг, отмечающий начало координат с вертикальным и горизонтальным перекрестием, чтобы идеально выровнять исходную точку на вершине.

Совместите горизонтальный край исходной точки с одним из краев угла так, чтобы другой край угла доходил до измерений вдоль изогнутого края, как показано на изображении выше.

Шаг 3. Найдите угол в градусах

Существует три типа углов, которые вы можете найти с помощью транспортира: острый , тупой и правый . ^[3]

Острый угол — это меньший угол, где линия пересекает другую, или технически любой угол, который меньше 90 °.

Тупой угол — это больший угол, где линия пересекается с другой, или технически любой угол, превышающий 90 °.

Прямой угол — это угол, равный точно 90 °, что означает, что две линии точно перпендикулярны друг другу.

Как найти острый угол

Если бы одна линия пересекалась с другой линией, образующей два угла, острый угол был бы меньшим углом. Выровняв исходную точку транспортира по вершине угла, а горизонтальный край выровнен с одной из линий, найдите отметку вдоль кривой в месте пересечения линии.

Если острый угол находится слева, отметка будет на внешней или самой внешней кромке транспортира.Если острый угол находится справа, отметка будет на внутренней стороне кривой.

На транспортире есть два ряда делений, позволяющих измерять градусы угла слева или справа. Измерения должны увеличиваться в направлении, в котором вы измеряете.

Как найти тупой угол

Если бы одна линия пересекалась с другой линией, образующей два угла, тупой угол был бы большим углом.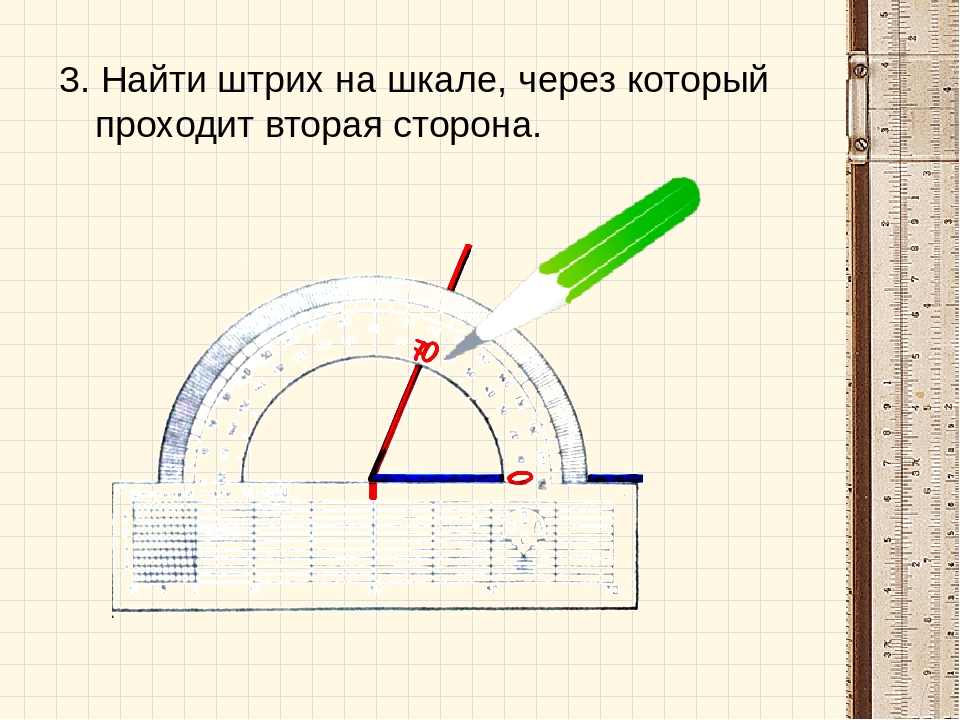 Выровняв исходную точку транспортира по вершине угла, а горизонтальный край выровнен с одной из линий, найдите отметку вдоль кривой в месте пересечения линии.

Если тупой угол слева, отметка будет на внешней или самой внешней кромке транспортира. Если тупой угол справа, отметка будет на внутренней стороне кривой.

Как нарисовать угол с помощью транспортира

Транспортиры также отлично подходят для рисования точных углов. Следуйте инструкциям, чтобы узнать, как это сделать.

Шаг 1. Нарисуйте базовую линию

Первый шаг — провести прямую линию на листе бумаги с помощью прямого края.Это базовая линия или плечо угла

Шаг 2: Нарисуйте вершину

Далее нарисуйте вершину угла в конце линии.

Шаг 3. Совместите транспортир по вершине

Теперь совместите начало координат транспортира с вершиной на линии, затем совместите базовую линию угла с линией в нижней части транспортира.

Шаг 4. Найдите угловую метку

Следующий шаг — найти отметку, соответствующую тупому или острому углу, который вы хотите нарисовать.Сделайте отметку на бумаге как можно ближе к отметке.

Шаг 5: Завершите угол

Наконец, завершите линию, соединив вершину и отметку угла, которую вы только что добавили, с помощью прямого края транспортира или линейки.

Полезные угловые инструменты

Поскольку большинство транспортиров имеют измерения в градусах, часто необходимо использовать формулу для преобразования ваших измерений в радианы, милы или грады. Воспользуйтесь нашим инструментом преобразования углов, чтобы преобразовать градусы в радианы, милы или грады.

Если вам нужен транспортир, вы можете скачать и распечатать наш транспортир для печати.

Как измерить угол круговой диаграммы

Что такое круговая диаграмма?

Круговая диаграмма — это статистическая круговая иллюстрация. Он разделен на сегменты для обозначения числовых пропорций различных величин. Он показывает распределение данных, которые имеют дискретный набор.

Каждый сегмент круговой диаграммы представляет определенную долю от общего количества.Значение каждого среза указывается в процентах или в форме угла.

Поскольку круговая диаграмма круговая, общий угол, соответствующий всему набору данных, составляет 360 градусов, что равно одному полному круговому повороту.

В этом руководстве мы научим вас, как измерить угол сегмента круговой диаграммы на основе заданных наборов данных или процентов, чтобы узнать реальное числовое значение величины. Итак, приступим!

Измерение угла круговой диаграммы: пошаговое руководство

В этом разделе вы узнаете, как измерить угол круговой диаграммы на двух рабочих примерах.

Рабочий пример №1 — напитки:

Предположим, что в классе университета 150 студентов. Их всех опросили и спросили об их любимом напитке (безалкогольном), который они любят пить постоянно. Были получены следующие ответы:

Напитки
Процент респондентов
Кофе
30%
Чай
20%
Газировка
30%
Вода
10%
Другое
10%

Теперь, если я спрошу Сколько студентов предпочитают чай, вы должны сделать следующий расчет и дать мне свой ответ:

Количество студентов, которые предпочитают чай = 20% × 150 студентов
= 20/100 x 150
= 30 студентов

Аналогично, для каждого напитка вы можете произвести расчет, аналогичный приведенному выше, и получить свой ответ.

Если затем вас попросят построить круговую диаграмму, отображающую собранную вами информацию о студентах и ​​напитках, вам следует сделать следующее:

Шаг 1 — Рассчитайте точное количество студентов, которые предпочитают каждый напиток:

Кофе:

30/100 × 150 = 45 студентов

Чай:

20/100 × 150 = 30 студентов

Сода:

30/100 × 150 = 45 студентов

Вода :

10/100 × 150 = 15 студентов

Другие:

10/100 × 150 = 15 студентов

Шаг 2 — Рассчитайте угол каждого сегмента / среза круговой диаграммы по формуле:

Угол среза = частота данных / общая частота × 360 градусов

Давайте воспользуемся этой формулой в нашем примере напитков.Мы знаем, что 45 студентов любят кофе, поэтому угол сегмента круговой диаграммы, который обозначает потребителей кофе, будет:

Угол сегмента кофе = люди, которые предпочитают кофе / общее количество опрошенных студентов × 360 градусов = 45/150 × 360 ° = 108 градусов

Таким же образом теперь вы можете рассчитать углы в градусах для каждого напитка, прежде чем переходить к построению круговой диаграммы:

Кофе:

45/150 × 360 ° = 108 °

Чай:

30/150 × 360 ° = 72 °

Сода:

45/150 × 360 ° = 108 °

Вода:

15/150 × 360 ° = 36 °

Другое:

15/150 × 360 ° = 36 °

Шаг 3 — Нарисуйте круговую диаграмму с использованием углов:

Когда у вас есть все углы, вы можете нарисовать круговую диаграмму.Обязательно пометьте все сегменты названиями напитков и укажите проценты или углы в градусах внутри ломтиков. Вот и все! Ваша круговая диаграмма готова.

Рабочий пример № 2 — Транспорт:

Предположим, вы провели опрос 100 человек для школьного проекта и спросили их, какой вид транспорта они предпочитают. Вы дали им 5 вариантов выбора: автомобиль, автобус, такси, метро и другие. Вы представили свои результаты своему другу в виде круговой диаграммы, как показано ниже:

КЛЮЧ
‍ Автомобиль
Автобус
Такси
Метро
Другое

У вашего друга нет другой информации, кроме этой круговой диаграммы, и он должен представить данные в табличной форме с дискретными числовыми значениями вашему учителю.Давайте посмотрим, какие шаги он должен предпринять:

Шаг 1. Измерьте угол круговой диаграммы:

Измерьте угол каждого сегмента круговой диаграммы. Держите прямую линию 0 °, отмеченную на транспортире на одной из прямых сторон сегмента, и считайте градусы, отмеченные на транспортире на другой прямой стороне сегмента. Ответ — угол сегмента или среза. Повторите этот шаг для каждого сегмента круговой диаграммы, пока не получите ответ в градусах для каждого вида транспорта.

Шаг 2 — Расчет частоты данных:

Используя приведенную ниже формулу, вычислите частоту в дискретных значениях:

Частота данных = (угол сектора ÷ 360 градусов) × общая частота

Использование эта формула для каждого вида транспорта, чтобы получить количество людей, которые его предпочли. Предположим, ваш друг рассчитал, что сегмент Метро составляет 90 градусов:

Количество людей, которые предпочли ездить на автобусе = (угол ÷ 360 °) × общее количество опрошенных людей
= (90 ° ÷ 360 °) × 100
= 25 люди предпочитали ездить на метро

Шаг 3 — Постройте таблицу, используя данные:

Как только ваш друг узнает точное количество людей, которые предпочли тот или иной вид транспорта, он может представить результаты вашему учителю следующим образом табличная форма:

Вид транспорта
No.людей, которые предпочли
‍ Автомобиль
xx
Автобус
xx
Такси
xx
Метро
25
Другое
xx
ВСЕГО
100

Мы надеялись, что вам понравилось наше подробное руководство о том, как построить и измерить угол круговая диаграмма. Посетите наш сайт, чтобы увидеть больше таких лекций и стать профессионалом в статистических иллюстрациях уже сегодня!

Тригонометрия: измерение углов

Мы определяем угол как объединение двух неколлинеарных лучей, имеющих общую начальную точку.Два луча называются плечами угла, а общая начальная точка называется его вершиной.

Мы можем интерпретировать угол, вращая луч из одного положения в другое. Когда мы используем эту интерпретацию угла, луч, с которого начинается, называется начальной стороной, а конечное положение луча называется конечной стороной, как показано на рисунке.