Основные формулы для расчета прогиба балки

Балка является основным элементом несущей конструкции сооружения. При строительстве важно провести расчет прогиба балки. В реальном строительстве на данный элемент действует сила ветра, нагружение и вибрации. Однако при выполнении расчетов принято принимать во внимание только поперечную нагрузку или проведенную нагрузку, которая эквивалентна поперечной.

Балки в доме

При расчете балка воспринимается как жесткозакрепленный стержень, который устанавливается на двух опорах. Если она устанавливается на трех и более опорах, расчет ее прогиба является более сложным, и провести его самостоятельно практически невозможно. Основное нагружение рассчитывается как сумма сил, которые действуют в направлении перпендикулярного сечения конструкции. Расчетная схема требуется для определения максимальной деформации, которая не должна быть выше предельных значений. Это позволит определить оптимальный материал необходимого размера, сечения, гибкости и других показателей.

Виды балок

Для строительства различных сооружений применяются балки из прочных и долговечных материалов. Такие конструкции могут отличаться по длине, форме и сечению. Чаще всего используются деревянные и металлические конструкции. Для расчетной схемы прогиба большое значение имеет материал элемента. Особенность расчета прогиба балки в данном случае будет зависеть от однородности и структуры ее материала.

Деревянные

Для постройки частных домов, дач и другого индивидуального строительства чаще всего используются деревянные балки. Деревянные конструкции, работающие на изгиб, могут использоваться для потолочных и напольных перекрытий.

Деревянные перекрытия

Для расчета максимального прогиба следует учитывать:

1. Материал. Различные породы дерева обладают разным показателем прочности, твердости и гибкости.
2. Форма поперечного сечения и другие геометрические характеристики.
3. Различные виды нагрузки на материал.

Допустимый прогиб балки учитывает максимальный реальный прогиб, а также возможные дополнительные эксплуатационные нагрузки.

Конструкции из древесины хвойных пород

Стальные

Металлические балки отличаются сложным или даже составным сечением и чаще всего изготавливаются из нескольких видов металла. При расчете таких конструкций требуется учитывать не только их жесткость, но и прочность соединений.

Стальные перекрытия

Металлические конструкции изготавливаются путем соединения нескольких видов металлопроката, используя при этом такие виды соединений:

• электросварка;
• заклепки;
• болты, винты и другие виды резьбовых соединений.

Стальные балки чаще всего применяются для многоэтажных домов и других видов строительства, где требуется высокая прочность конструкции. В данном случае при использовании качественных соединений гарантируется равномерно распределенная нагрузка на балку.

Для проведения расчета балки на прогиб может помочь видео: 

Прочность и жесткость балки

Чтобы обеспечить прочность, долговечность и безопасность конструкции, необходимо выполнять вычисление величины прогиба балок еще на этапе проектирования сооружения. Поэтому крайне важно знать максимальный прогиб балки, формула которого поможет составить заключение о вероятности применения определенной строительной конструкции.

Использование расчетной схемы жесткости позволяет определить максимальные изменения геометрия детали. Расчет конструкции по опытным формулам не всегда эффективен. Рекомендуется использовать дополнительные коэффициенты, позволяющие добавить необходимый запас прочности. Не оставлять дополнительный запас прочности – одна из основных ошибок строительства, которая приводит к невозможности эксплуатации здания или даже тяжелым последствиям.

Существует два основных метода расчета прочности и жесткости:

1. Простой. При использовании данного метода применяется увеличительный коэффициент.
2. Точный. Данный метод включает в себя использование не только коэффициентов для запаса прочности, но и дополнительные вычисления пограничного состояния.

Последний метод является наиболее точным и достоверным, ведь именно он помогает определить, какую именно нагрузку сможет выдержать балка.

Расчет балок на прогиб

Расчет на жесткость

Для расчета прочности балки на изгиб применяется формула:

Где:

M – максимальный момент, который возникает в балке;

W_n,min – момент сопротивления сечения, который является табличной величиной или определяется отдельно для каждого вида профиля.

R_y является расчетным сопротивлением стали при изгибе. Зависит от вида стали.

γ_c представляет собой коэффициент условий работы, который является табличной величиной.

Расчет жесткости или величины прогиба балки является достаточно простым, поэтому расчеты может выполнить даже неопытный строитель. Однако для точного определения максимального прогиба необходимо выполнить следующие действия:

1. Составление расчетной схемы объекта.
2. Расчет размеров балки и ее сечения.
3. Вычисление максимальной нагрузки, которая воздействует на балку.
4. Определение точки приложения максимальной нагрузки.
5. Дополнительно балка может быть проверена на прочность по максимальному изгибающему моменту.
6. Вычисление значения жесткости или максимально прогиба балки.

Чтобы составить расчетную схему, потребуются такие данные:

• размеры балки, длину консолей и пролет между ними;
• размер и форму поперечного сечения;
• особенности нагрузки на конструкцию и точно ее приложения;
• материал и его свойства.

Если производится расчет двухопорной балки, то одна опора считается жесткой, а вторая – шарнирной.

Расчет моментов инерции и сопротивления сечения

Для выполнения расчетов жесткости потребуется значение момент инерции сечения (J) и момента сопротивления (W). Для расчета момента сопротивления сечения лучше всего воспользоваться формулой:

Важной характеристикой при определении момента инерции и сопротивления сечения является ориентация сечения в плоскости разреза. При увеличении момента инерции увеличивается и показатель жесткости.

Определение максимальной нагрузки и прогиба

Для точного определения прогиба балки, лучше всего применять данную формулу:

Где:

q является равномерно-распределенной нагрузкой;

E – модуль упругости, который является табличной величиной;

l – длина;

I – момент инерции сечения.

Чтобы рассчитать максимальную нагрузку, следует учитывать статические и периодические нагрузки. К примеру, если речь идет о двухэтажном сооружении, то на деревянную балку будет постоянно действовать нагрузка от ее веса, техники, людей.

Особенности расчета на прогиб

Расчет на прогиб проводится обязательно для любых перекрытий. Крайне важен точный расчет данного показателя при значительных внешних нагрузках. Сложные формулы в данном случае использовать необязательно. Если использовать соответствующие коэффициенты, то вычисления можно свести к простым схемам:

1. Стержень, который опирается на одну жесткую и одну шарнирную опору, и воспринимает сосредоточенную нагрузку.
2. Стержень, который опирается на жесткую и шарнирную опору, и при этом на него действует распределенное нагружение.
3. Варианты нагружения консольного стержня, который закреплен жестко.
4. Действие на конструкцию сложной нагрузки.

Применение этого метода вычисления прогиба позволяет не учитывать материал. Поэтому на расчеты не влияют значения его основных характеристик.

Пример подсчета прогиба

Чтобы понять процесс расчета жесткости балки и ее максимального прогиба, можно использовать простой пример проведения расчетов. Данный расчет проводится для балки с такими характеристиками:

• материал изготовления – древесина;
• плотность составляет 600 кг/м3;
• длина составляет 4 м;
• сечение материала составляет 150*200 мм;
• масса перекрывающих элементов составляет 60 кг/м²;
• максимальная нагрузка конструкции составляет 249 кг/м;
• упругость материала составляет 100 000 кгс/ м²;
• J равно 10 кг*м².

Для вычисления максимальной допустимой нагрузки учитывается вес балки, перекрытий и опор. Рекомендуется также учесть вес мебели, приборов, отделки, людей и других тяжелых вещей, который также будут оказывать воздействие на конструкцию. Для расчета потребуются такие данные:

• вес одного метра балки;
• вес м2 перекрытия;
• расстояние, которое оставляется между балками;
• временная нагрузка;
• нагрузка от перегородок на перекрытие.

Чтобы упросить расчет данного примера, можно принять массу перекрытия за 60 кг/м², нагрузку на каждое перекрытие за 250 кг/м², нагрузки на перегородки 75 кг/м², а вес метра балки равным 18 кг. При расстоянии между балками в 60 см, коэффициент k будет равен 0,6.

Если подставить все эти значения в формулу, то получится:

q = ( 60 + 250 + 75 ) * 0,6 + 18 = 249 кг/м.

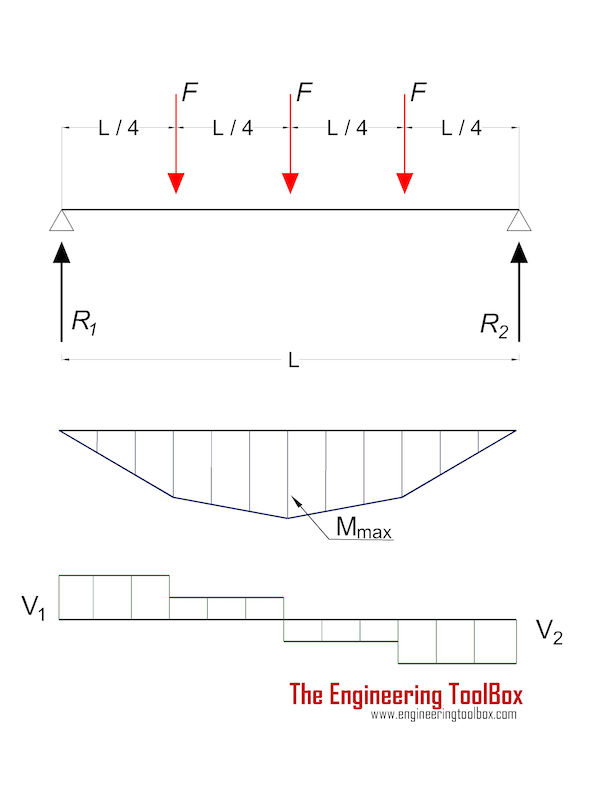
Для расчета изгибающего момента следует воспользоваться формулой f = (5 / 384) * [(qn * L4) / (E * J)] £ [¦].

Подставив в нее данные, получается f = (5 / 384) * [(qn * L4) / (E * J)] = (5 / 384) * [(249 * 44) / (100 000 * 10)] = 0,13020833 * [(249 * 256) / (100 000 * 10)] = 0,13020833 * (6 3744 / 10 000 000) = 0,13020833 * 0,0000063744 = 0,00083 м = 0,83 см.

Именно это и является показателем прогиба при воздействии на балку максимальной нагрузки. Данные расчеты показывают, что при действии на нее максимальной нагрузки, она прогнется на 0,83 см. Если данный показатель меньше 1, то ее использование при указанных нагрузках допускается.

Использование таких вычислений является универсальным способом вычисления жесткости конструкции и величины их прогибания. Самостоятельно вычислить данные величины достаточно легко. Достаточно знать необходимые формулы, а также высчитать величины. Некоторые данные необходимо взять в таблице. При проведении вычислений крайне важно уделять внимание единицам измерения. Если в формуле величина стоит в метрах, то ее нужно перевести в такой вид. Такие простые ошибки могут сделать расчеты бесполезными. Для вычисления жесткости и максимального прогиба балки достаточно знать основные характеристики и размеры материала. Эти данные следует подставить в несколько простых формул.

 

Распределенная нагрузка на балку ℹ️ определение, формулы и условия расчета равномерно и неравномерно распределенной нагрузки, примеры вычисления момента

Взаимодействия с деталями, отдельными элементами и конструкциями механизма задается с помощью нагрузок. В плоскости задается интенсивность взаимодействия конструкции по длине, а в пространстве – по её площади.

Распределённая нагрузка на балку задается площадью, обозначается буквой q и измеряется в [H/м³] для объемной конструкции, в [H/м²] — для площади, для линейной – в [H/м].

Продемонстрируем это на рисунке:

Нагрузку также можно заменить тягой, рассредоточенной по всей поверхности. Значение определяется по формуле:

Q = q ∗ AB⌈H⌉

здесь AB является тяжестью, q – интенсивностью, которая измеряется в [H/м].

Примечательно, что сила приложена к середине данного отрезка AB.

На данном рисунке представлен расчёт возрастающей нагрузки, которую можно заменить равнодействующей единицей, рассчитываемое по формуле:

Q = q_max ∗ AB/2

где q_max – максимальная интенсивность [Н/м]. 

Q приложена к точке C, где AC равно: AC = 2/3 AB 

Рассматривая функцию q(x), представленную на рисунке:

можно высчитать значение эквивалентной силы по формуле:

Равномерно и неравномерно распределенная нагрузка на балку

Распределение сил, которые лежат в одной плоскости, задается равномерно распределенной тяжестью. Основным обозначением является интенсивность q — предельная тяга, несущая равнодействующую на единицу длины нагруженного участка АВ длиной а. 

Единицы измерения распределённой нагрузки [Н/м].

Её также можно заменить на величину Q, которая приложена в середину AB. 

Составим формулу: Q = q∗a

Неравномерно распределённую нагрузку чаще всего упрощают, приводя её к эквивалентной равномерно распределенной, чтобы упростить расчеты.

При построении также следует учитывать максимальный прогиб балки, её прочность, расчетную опорную реакцию и моментальную опору.

Пример решения задач с распределенной нагрузкой

Рассмотрим пример распределенной нагрузки на балку. Им может послужить тяга, благодаря которой происходит разрыв стальной стенки баллона с некоторым газом.

Для начала определяем результирующую давления в металлической трубе. Интенсивность равна q, радиус этого сектора трубы – R, ось симметрии Оx, а 2α – это центральный угол. Представим это на рисунке:

Выделим элемент сектора трубы ∆ϕ.

Затем определим единицу силы ∆Q. Она действует на плоскость дуги. Составим формулу:

Проекция результирующей тяги на ось Оx является:

Исходя из вышесказанного, можно найти проекцию этой же силы на ось Оy:

AB является хордой, которая стягивает дугу.

В нашей задаче сосуд – это ёмкость цилиндрической формы с высотой H, внутренним давлением P, действующим на стенки, и нагрузкой q = p [Н/м²]. 

Разделим цилиндр вдоль его диаметра. 

Исходя из этого, равнодействующая результирующих сил определяется по формуле:

где d – это внутренний диаметр цилиндра, h — его высота. 

Формулу также можно записать следующим образом:

Итак, почему баллон имеет способность разрываться? На его стенки действуют значения S1, S2, S3 (площади), а также F, p (плотность), h (высота цилиндра) и R (его радиус). Рассчитаем их по формулам:

 

Изобразим баллон в момент разрыва:

Учтём a – толщину ёмкости. Таким образом напряжение, которое растягивает баллон, (усилия распространяются в том числе на крышку и дно цилиндра) равно:

Важную роль при решении практических задач также играет эпюра распределенной нагрузки – плоская фигура, которая ограничена графиком. Величина, действующая на балку, называется интенсивностью – силой, которая распространяется на единицы площади, объема или длины.

Расчет металлической балки на прогиб: учимся составлять формулы

Приветствую тебя, читатель экспресс-курса — «сопромат для чайников» на сайте – SoproMats.ru. Меня зовут Константин Вавилов, я являюсь автором статей по сопромату и других материалов данного ресурса. В этой статье, будем рассматривать универсальную методику расчета прогибов балки — метод начальных параметров. Как и любая другая статья для чайников, на нашем проекте, этот материал будет изложен максимально просто, лаконично и без лишних заумных терминов.

В качестве примера, возьмем металлическую балку на двух опорах. Запишем для нее формулу для вычисления прогиба, посчитаем его численное значение. И также в конце этой статьи дам ссылки на другие полезные статьи с примерами определения прогибов для различных расчетных схем.

Что такое прогиб балки?

Под действием внешней нагрузки, поперечные сечения балки перемещаются вертикально (вверх или вниз), эти перемещения называются прогибами. Сопромат позволяет нам определить прогиб балки, зная ее геометрические параметры: длину, размеры поперечного сечения. И также нужно знать материал, из которого изготовлена балка (модуль упругости).

Кстати! Помимо вертикальных перемещений, поперечные сечения балки, поворачиваются на определенный угол. И эти величины также можно определить методом начальных параметров.

ν-прогиб сечения C; θ-угол поворота сечения C.

Прогибы балки необходимо рассчитывать, при расчете на жесткость. Расчётные значения прогибов не должны превышать допустимых значений. Если расчетное значение меньше, чем допустимое, то считают, что условие жесткости элемента конструкции соблюдается. Если же нет, то принимаются меры по повышению жесткости. Например, задаются другим материалом, у которого модуль упругости БОЛЬШЕ. Либо же меняют геометрические параметры балки, чаще всего, поперечное сечение. Например, если балка двутаврового профиля №12, не подходит по жесткости, принимают двутавр №14 и делают перерасчет. Если потребуется, повторяют подбор, до того момента пока не найдут тот самый – двутавр.

Метод начальных параметров

Метод начальных параметров, является довольно универсальным и простым методом. Используя этот метод можно записывать формулу для вычисления прогиба и угла поворота любого сечения балки постоянной жесткости (с одинаковым поперечным сечением по длине.)

Под начальными параметрами понимаются уже известные перемещения:

• в опорах прогибы равны нулю;
• в жесткой заделке прогиб и угол поворота сечения равен нулю.

Учитывая эти хитрости, их называют еще граничными условиями, определяются перемещения в других частях балки.

Расчет прогибов балки

Посмотрим, как пользоваться методом начальных параметров на примере простой балки, которая загружена всевозможными типами нагрузок, чтобы максимально охватить все тонкости этого метода:

Реакции опор

Для расчета нужно знать все внешние нагрузки, действующие на балку, в том числе и реакции, возникающие в опорах.

Если ты не знаешь, как определять реакции, то рекомендую изучить данный материал, где я как раз рассказываю, как они определяются на примере этой балки:

Система координат

Далее вводим систему координат, с началом в левой части балки (точка А):

Распределенная нагрузка

Метод начальных параметров, который будем использовать чуть позднее, работает только в том случае, когда распределенная нагрузка доходит до крайнего правого сечения, наиболее удаленного от начала системы координат. Конкретно, в нашем случае, нагрузка обрывается и такая расчетная схема неприемлема для дальнейшего расчета.

Если бы нагрузка была приложена вот таким способом:

То можно было бы сразу приступать к расчету перемещений. Нам же потребуется использовать один хитрый прием – ввести дополнительные нагрузки, одна из которых будет продолжать действующую нагрузку q, другая будет компенсировать это искусственное продолжение. Таким образом, получим эквивалентную расчетную схему, которую уже можно использовать в расчете методом начальных параметров:

Вот, собственно, и все подготовительные этапы, которые нужно сделать перед расчетом.

Приступим непосредственно к самому расчету прогиба балки. Рассмотрим наиболее интересное сечение в середине пролета, очевидно, что это сечение прогнется больше всех и при расчете на жесткость такой балки, рассчитывалось бы именно это сечение. Обзовем его буквой – C:

Относительно системы координат записываем граничные условия. Учитывая способ закрепления балки, фиксируем, что прогибы в точках А и В равны нулю, причем важны расстояния от начала координат до опор:

\[ { V }_{ A }=0\quad при\quad x=0 \]

\[ { V }_{ B }=0\quad при\quad x=8м \]

Записываем уравнение метода начальных параметров для сечения C:

\[ E{ I }_{ z }{ V }_{ C }=… \]

Произведение жесткости балки EI и прогиба сечения C будет складываться из произведения EI и прогиба сечения в начале системы координат, то есть сечения A:

\[ E{ I }_{ z }{ V }_{ C }=E{ I }_{ z }{ V }_{ A }+ … \]

Напомню, E – это модуль упругости первого рода, зависящий от материала из которого изготовлена балка, I – это момент инерции, который зависит от формы и размеров поперечного сечения балки. Также учитывается угол поворота поперечного сечения в начале системы координат, причем угол поворота дополнительно умножается на расстояние от рассматриваемого сечения до начала координат:

\[ E{ I }_{ z }{ V }_{C }=E{ I }_{ z }{ V }_{ A }+E{ I }_{ z }{ \theta }_{ A }\cdot 4+… \]

Учет внешней нагрузки

И, наконец, нужно учесть внешнюю нагрузку, но только ту, которая находится левее рассматриваемого сечения C. Здесь есть несколько особенностей:

• Сосредоточенные силы и распределенные нагрузки, которые направленны вверх, то есть совпадают с направлением оси y, в уравнении записываются со знаком «плюс». Если они направленны наоборот, соответственно, со знаком «минус»:

• Моменты, направленные по часовой стрелке – положительные, против часовой стрелки – отрицательные:

• Все сосредоточенные моменты нужно умножать дробь:

\[ M\cdot \frac { { x }^{ 2 } }{ 2 } \]

• Все сосредоточенные силы нужно умножать дробь:

\[ F\cdot \frac { { x }^{ 3 } }{ 6 } \]

• Начало и конец распределенных нагрузок нужно умножать на дробь:

\[ q\cdot \frac { { x }^{ 4 } }{ 24 } \]

Откуда такие цифры и степени взялись? Все эти вещи вытекают при интегрировании дифференциального уравнения упругой линии балки, в методе начальных параметров все эти выводы опускаются, то есть он является как бы упрощенным и универсальным методом.

Формулы прогибов

С учетом всех вышеописанных правил запишем окончательное уравнение для сечения C:

\[ E{ I }_{ z }{ V }_{ C }=E{ I }_{ z }{ V }_{ A }+E{ I }_{ z }{ \theta }_{ A }\cdot 4+\frac { { R }_{ A }\cdot { 4 }^{ 3 } }{ 6 } -\frac { F\cdot { 4 }^{ 3 } }{ 6 } -\frac { q\cdot { 2 }^{ 4 } }{ 24 } \]

В этом уравнении содержится 2 неизвестные величины – искомый прогиб сечения C и угол поворота сечения A.

Поэтому, чтобы найти прогиб, составим второе уравнение для сечения B, из которого можно определить угол поворота сечения A. Заодно закрепим пройденный материал:

\[ E{ I }_{ z }{ V }_{ B }=E{ I }_{ z }{ V }_{ A }+E{ I }_{ z }{ \theta }_{ A }\cdot 8+\frac { { R }_{ A }\cdot { 8 }^{ 3 } }{ 6 } -\frac { F\cdot { 8 }^{ 3 } }{ 6 } -\frac { q\cdot 6^{ 4 } }{ 24 } +\frac { q\cdot 2^{ 4 } }{ 24 } =0 \]

Упрощаем уравнение:

\[ E{ I }_{ z }{ \theta }_{ A }\cdot 8+874.67=0 \]

Выражаем угол поворота:

\[ { \theta }_{ A }=-\frac { 874.67 }{ 8E{ I }_{ z } } =-\frac { 109.33кН{ м }^{ 2 } }{ E{ I }_{ z } } \]

Подставляем это значение в наше первое уравнение и находим искомое перемещение:

\[ E{ I }_{ z }{ V }_{ C }=\frac { -109.33\cdot 4E{ I }_{ z } }{ E{ I }_{ z } } +\frac { { R }_{ A }\cdot { 4 }^{ 3 } }{ 6 } -\frac { F\cdot { 4 }^{ 3 } }{ 6 } -\frac { q\cdot { 2 }^{ 4 } }{ 24 } =-\frac { 280кН{ м }^{ 3 } }{ E{ I }_{ z } } \]

Вычисление прогиба

Значение получили в общем виде, так как изначально не задавались тем, какое поперечное сечение имеет рассчитываемая балка. Представим, что металлическая балка имеет двутавровое поперечное сечение №30. Тогда:

\[ { V }_{ C }=-\frac { 280кН{ м }^{ 3 } }{ E{ I }_{ z } } =-\frac { 280\cdot { 10 }^{ 9 }Н\cdot { см }^{ 3 } }{ 2\cdot { 10 }^{ 7 }\frac { Н }{ { см }^{ 2 } } \cdot 7080{ см }^{ 4 } } =-2см \]

Таким образом, такая балка прогнется максимально на 2 см. Знак «минус» указывает на то, что сечение переместится вниз.

На этом, пожалуй, закончу данный урок. Если у вас возникли какие-либо вопросы по представленным материалам, задавайте вопросы в комментариях к этой статье. А также рекомендую вам посмотреть другие примеры определение прогибов этим методом. Там вы найдете более сложные задачи, определение углов поворотов, примеры расчета консольных балок (с жесткой заделкой).

Расчет балки на прогиб

Однопролетные балки на двух шарнирных опорах
1	Расчет балки на двух шарнирных опорах при одной сосредоточенной нагрузке	Смотреть расчет
2	Расчет балки на двух шарнирных опорах при двух сосредоточенных нагрузках	Смотреть расчет
3	Расчет балки на двух шарнирных опорах при одной равномерно-распределенной нагрузке	Смотреть расчет
4	Расчет балки на двух шарнирных опорах при одной неравномерно-распределенной нагрузке	Смотреть расчет
5	Расчет балки на двух шарнирных опорах при действии изгибающего момента	Смотреть расчет
Балки с жестким защемлением на двух опорах
6	Расчет балки с жестким защемлением на опорах при одной сосредоточенной нагрузке	Смотреть расчет
7	Расчет балки с жестким защемлением на опорах при двух сосредоточенных нагрузках	Смотреть расчет
8	Расчет балки с жестким защемлением на опорах при одной равномерно-распределенной нагрузке	Смотреть расчет
9	Расчет балки с жестким защемлением на опорах при одной неравномерно-распределенной нагрузке	Смотреть расчет
10	Расчет балки с жестким защемлением на опорах при действии изгибающего момента	Смотреть расчет
Балки с жестким защемлением на одной опоре (консольные)
11	Расчет однопролетной балки с жестким защемлением на одной опоре при одной сосредоточенной нагрузке	Смотреть расчет
12	Расчет однопролетной балки с жестким защемлением на одной опоре при одной равномерно-распределенной нагрузке	Смотреть расчет
13	Расчет однопролетной балки с жестким защемлением на одной опоре при одной неравномерно-распределенной нагрузке	Смотреть расчет
14	Расчет однопролетной балки с жестким защемлением на одной опоре при действии изгибающего момента	Смотреть расчет
Балки двухпролетные
15	Расчет двухпролетной с шарнирными опорами при одной сосредоточенной нагрузке	Смотреть
16	Расчет двухпролетной с шарнирными опорами при двух сосредоточенных нагрузках	Смотреть
17	Расчет двухпролетной с шарнирными опорами при одной равномерно-распределенной нагрузке	Смотреть
18	Расчет двухпролетной с шарнирными опорами при одной неравномерно-распределенной нагрузке	Смотреть
19	Расчет двухпролетной с шарнирными опорами при одной неравномерно-распределенной нагрузке	Смотреть

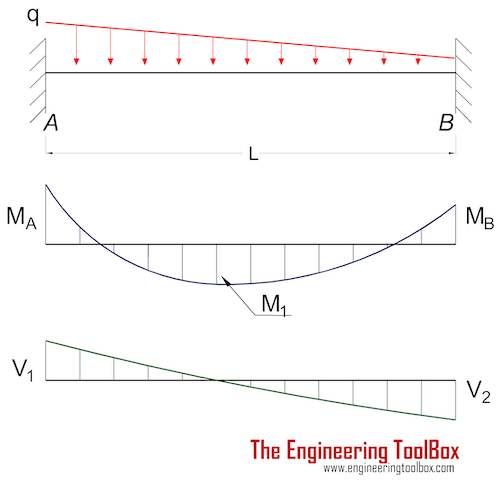
Расчет балок на прогиб. Максимальный прогиб балки: формула

Балка – элемент в инженерии, представляющий собой стержень, который нагружают силы, действующие в направлении, перпендикулярном стержню. Деятельность инженеров зачастую включает в себя необходимость расчета прогиба балки под нагрузкой. Этой действие выполняется для того, чтобы ограничить максимальный прогиб балки.

Типы

На сегодняшний день в строительстве могут использоваться балки, изготовленные из разных материалов. Это может быть металл или дерево. Каждый конкретный случай подразумевает под собой разные балки. При этом расчет балок на прогиб может иметь некоторые отличия, которые возникают по принципу разницы в строении и используемых материалов.

Деревянные балки

Сегодняшнее индивидуальное строительство подразумевает под собой широкое применение балок, изготовленных из дерева. Практически каждое строение содержит в себе деревянные перекрытия. Балки из дерева могут использоваться как несущие элементы, их применяют при изготовлении полов, а также в качестве опор для перекрытий между этажами.

Ни для кого не секрет, что деревянная, так же как и стальная балка, имеет свойство прогибаться под воздействием нагрузочных сил. Стрелка прогиба зависит от того, какой материал используется, геометрических характеристик конструкции, в которой используется балка, и характера нагрузок.

Допустимый прогиб балки формируется из двух факторов:

• Соответствие прогиба и допустимых значений.
• Возможность эксплуатации здания с учетом прогиба.

Проводимые при строительстве расчеты на прочность и жесткость позволяют максимально эффективно оценить то, какие нагрузки сможет выдерживать здание в ходе эксплуатации. Также эти расчеты позволяют узнать, какой именно будет деформация элементов конструкции в каждом конкретном случае. Пожалуй, никто не будет спорить с тем, что подробные и максимально точные расчеты – это часть обязанностей инженеров-строителей, однако с использованием нескольких формул и навыка математических вычислений можно рассчитать все необходимые величины самостоятельно.

Для того чтобы произвести правильный расчет прогиба балки, нужно также брать во внимание тот факт, что в строительстве понятия жесткости и прочности являются неразрывными. Опираясь на данные расчета прочности, можно приступать к дальнейшим расчетам относительно жесткости. Стоит отметить, что расчет прогиба балки – один из незаменимых элементов расчета жесткости.

Обратите ваше внимание на то, что для проведения таких вычислений самостоятельно лучше всего использовать укрупненные расчеты, прибегая при этом к достаточно простым схемам. При этом также рекомендуется делать небольшой запас в большую сторону. Особенно если расчет касается несущих элементов.

Расчет балок на прогиб. Алгоритм работы

На самом деле алгоритм, по которому делается подобный расчет, достаточно прост. В качестве примера рассмотрим несколько упрощенную схему проведения расчета, при этом опустив некоторые специфические термины и формулы. Для того чтобы произвести расчет балок на прогиб, необходимо выполнить ряд действий в определенном порядке. Алгоритм проведения расчетов следующий:

• Составляется расчетная схема.
• Определяются геометрические характеристики балки.
• Вычисляется максимальную нагрузку на данный элемент.
• В случае возникновения необходимости проверяется прочность бруса по изгибающему моменту.
• Производится вычисление максимального прогиба.

Как видите, все действия достаточно просты и вполне выполнимы.

Составление расчетной схемы балки

Для того чтобы составить расчетную схему, не требуется больших знаний. Для этого достаточно знать размер и форму поперечного сечения элемента, пролет между опорами и способ опирания. Пролетом является расстояние между двумя опорами. К примеру, вы используете балки как опорные брусья перекрытия для несущих стен дома, между которыми 4 м, то величина пролета будет равна 4 м.

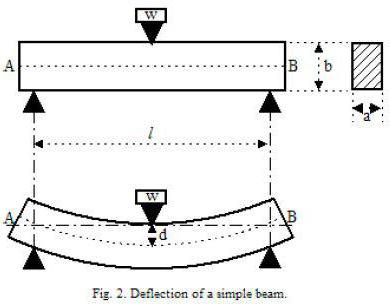
Вычисляя прогиб деревянной балки, их считают свободно опертыми элементами конструкции. В случае балки перекрытия для расчета принимается схема с нагрузкой, которая распределена равномерно. Обозначается она символом q. Если же нагрузка несет сосредоточенный характер, то берется схема с сосредоточенной нагрузкой, обозначаемой F. Величина этой нагрузки равна весу, который будет оказывать давление на конструкцию.

Момент инерции

Геометрическая характеристика, которая получила название момент инерции, важна при проведении расчетов на прогиб балки. Формула позволяет вычислить эту величину, мы приведем ее немного ниже.

При вычислении момента инерции нужно обращать внимание на то, что размер этой характеристики зависит от того, какова ориентация элемента в пространстве. При этом наблюдается обратно пропорциональная зависимость между моментом инерции и величиной прогиба. Чем меньше значение момента инерции, тем больше будет значение прогиба и наоборот. Эту зависимость достаточно легко отследить на практике. Каждый человек знает, что доска, положенная на ребро, прогибается гораздо меньше, чем аналогичная доска, находящаяся в нормальном положении.

Подсчет момента инерции для балки с прямоугольным сечением производится по формуле:

J=b*h^3/12, где:

b – ширина сечения;

h – высота сечения балки.

Вычисления максимального уровня нагрузки

Определение максимальной нагрузки на элемент конструкции производится с учетом целого ряда факторов и показателей. Обычно при вычислении уровня нагрузки берут во внимание вес 1 погонного метра балки, вес 1 квадратного метра перекрытия, нагрузку на перекрытие временного характера и нагрузку от перегородок на 1 квадратный метр перекрытия. Также учитывается расстояние между балками, измеренное в метрах. Для примера вычисления максимальной нагрузки на деревянную балку примем усредненные значения, согласно которым вес перекрытия составляет 60 кг/м², временная нагрузка на перекрытие равна 250 кг/м², перегородки будут весить 75 кг/м². Вес самой балки очень просто вычислить, зная ее объем и плотность. Предположим, что используется деревянная балка сечением 0,15х0,2 м. В этом случае ее вес будет составлять 18 кг/пог.м. Также для примера примем расстояние между брусьями перекрытия равным 600 мм. В этом случае нужный нам коэффициент составит 0,6.

В результате вычисления максимальной нагрузки получаем следующий результат: q=(60+250+75)*0,6+18=249 кг/м.

Когда значение получено, можно переходить к расчету максимального прогиба.

Вычисление значения максимального прогиба

Когда проводится расчет балки, формула отображает в себе все необходимые элементы. При этом стоит учитывать, что формула, используемая для расчетов, может иметь несколько иной вид, если расчет проводится для разных типов нагрузок, которые будут оказывать влияние на балку.

Сначала приведем вашему вниманию формулу, используемую для расчета максимального прогиба деревянной балки с распределенной нагрузкой.

f=-5*q*l^4/384*E*J.

Обратите внимание, что в данной формуле Е – это постоянная величина, которая получила название модуль упругости материала. Для древесины эта величина равна 100 000 кгс/ м².

Продолжив вычисления с нашими данными, использованными для примера, получим то, что для балки из древесины, сечение которой составляет 0,15х0,2 м, а длина равна 4 м, величина максимального прогиба при воздействии распределенной нагрузки равна 0,83 см.

Обращаем внимание, что когда производится расчет прогиба с учетом схемы с сосредоточенной нагрузкой, формула приобретает следующий вид:

f=-F*l^3/48*E*J, где:

F – сила давления на брус.

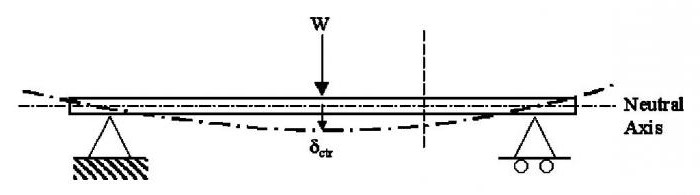
Также обращаем внимание на то, что значение модуля упругости, используемое в расчетах, может различаться для разных видов древесины. Влияние оказывают не только порода дерева, но и вид бруса. Поэтому цельная балка из дерева, клееный брус или оцилиндрованное бревно будут иметь разные модули упругости, а значит, и разные значения максимального прогиба.

Вы можете преследовать разные цели, совершая расчет балок на прогиб. Если вы хотите узнать пределы деформации элементов конструкции, то по завершении расчета стрелки прогиба вы можете остановиться. Если же ваша цель – установить уровень соответствия найденных показателей строительным нормам, то их нужно сравнить с данными, которые размещены в специальных документах нормативного характера.

Двутавровая балка

Обратите внимание на то, что балки из двутавра применяются несколько реже в силу их формы. Однако также не стоит забывать, что такой элемент конструкции выдерживает гораздо большие нагрузки, чем уголок или швеллер, альтернативой которых может стать двутавровая балка.

Расчет прогиба двутавровой балки стоит производить в том случае, если вы собираетесь использовать ее в качестве мощного элемента конструкции.

Также обращаем ваше внимание на то, что не для всех типов балок из двутавра можно производить расчет прогиба. В каких же случаях разрешено рассчитать прогиб двутавровой балки? Всего таких случаев 6, которые соответствуют шести типам двутавровых балок. Эти типы следующие:

• Балка однопролетного типа с равномерно распределенной нагрузкой.
• Консоль с жесткой заделкой на одном конце и равномерно распределенной нагрузкой.
• Балка из одного пролета с консолью с одной стороны, к которой прикладывается равномерно распределенная нагрузка.
• Однопролетная балка с шарнирным типом опирания с сосредоточенной силой.
• Однопролетная шарнирно опертая балка с двумя сосредоточенными силами.
• Консоль с жесткой заделкой и сосредоточенной силой.

Металлические балки

Расчет максимального прогиба одинаковый, будь это стальная балка или же элемент из другого материала. Главное — помнить о тех величинах, которые специфические и постоянные, как к примеру модуль упругости материала. При работе с металлическими балками, важно помнить, что они могут быть изготовлены из стали или же из двутавра.

Прогиб металлической балки, изготовленной из стали, вычисляется с учетом, что константа Е в данном случае составляет 2·105Мпа. Все остальные элементы, вроде момента инерции, вычисляются по алгоритмам, описанным выше.

Расчет максимального прогиба для балки с двумя опорами

В качестве примера рассмотрим схему, в которой балка находится на двух опорах, а к ней прикладывается сосредоточенная сила в произвольной точке. До момента прикладывания силы балка представляла собой прямую линию, однако под воздействием силы изменила свой вид и вследствие деформации стала кривой.

Предположим, что плоскость ХУ является плоскостью симметрии балки на двух опорах. Все нагрузки действуют на балку в этой плоскости. В этом случае фактом будет то, что кривая, полученная в результате действия силы, также будет находиться в этой плоскости. Данная кривая получила название упругой линии балки или же линии прогибов балки. Алгебраически решить упругую линию балки и рассчитать прогиб балки, формула которого будет постоянной для балок с двумя опорами, можно следующим образом.

Прогиб на расстоянии z от левой опоры балки при 0 ≤ z ≤ a

F(z)=(P*a²*b²)/(6E*J*l)*(2*z/a+z/b-z³/a²*b)

Прогиб балки на двух опорах на расстоянии z от левой опоры при а ≤ z ≤l

f(z)=(-P*a²*b²)/(6E*J*l)*(2*(l-z)/b+(l-z)/a-(l-z)³/a+b²), где Р – прикладываемая сила, Е – модуль упругости материала, J – осевой момент инерции.

В случае балки с двумя опорами момент инерции вычисляется следующим образом:

J=b₁h₁³/12, где b₁ и h₁ – значения ширины и высоты сечения используемой балки соответственно.

Заключение

В заключение можно сделать вывод о том, что самстоятельно вычислить величину максимального прогиба балки разных типов достаточно просто. Как было показано в этой статье, главное — знать некоторые характеристики, которые зависят от материала и его геометрических характеристик, а также провести вычисления по нескольким формулам, в которых каждый параметр имеет свое объяснение и не берется из ниоткуда.

Расчетные схемы для балок. Расчёт шарнирно-консольных балок на постоянную и подвижную нагрузки

Балка — это стержень или брус, работающий преимущественно на изгиб. Статически определимые балки разделяются на следующие типы (рис. 1.8):

простые балки — балки на двух опорах по концам;

консольные — балки на двух опорах со свешивающимися концами или консолями;

консоли — балки, защемлённые одним концом;

шарнирно-консольные балки, составленные из двух или нескольких последовательно расположенных балок, концы которых связаны между собой шарнирами.

Рис. 1.8. Различные типы балок: а – простая балка; б – консольная балка; в – консоль; г – шарнирно-консольная балка

Расстановка шарниров в многопролётной балке должна быть произведена так, чтобы она была статически определимой и геометрически неизменяемой:

в каждом пролёте должно быть размещено не более двух шарниров;

пролёты с двумя шарнирами должны быть размещены не менее чем через пролёт;

пролёты с одним шарниром могут следовать один за другим, если в системе есть одна неподвижная балка.

Консоль, простая балка и балка с консолями — это геометрически неизменяемые и статически определимые системы.

Длина консоли называется вылетом консоли, а длина простой балки – пролётом.

1.6. Порядок расчёта шарнирно-консольных балок

Подсчитывают степень свободы системы.

Проводят анализ геометрической неизменяемости системы. Изображают схему взаимодействия элементов шарнирно-консольной балки, то есть поэтажную схему, для чего мысленно разъединяют элементы балки, разделив их на основные или главные, которые могут самостоятельно воспринимать внешнюю нагрузку, и второстепенные или присоединённые, которые не могут работать самостоятельно, а должны опираться на основные балки в соответствии с рисунком 9.

Аналитический расчёт шарнирно-консольных балок начинают со второстепенной балки самого верхнего этажа. Построив для верхней балки эпюры изгибающихся моментов и поперечных сил, прикладывают реакцию опоры на нижележащую балку с обратным направлением и рассчитывают её. Последней рассчитывается опорная балка.

Признаки основной и второстепенной частей:

если разрушается основная часть, то разрушается вся система;

при разрушении второстепенной части, основная или главная остаётся без изменения.

Рис. 1.9. Поэтажные схемы шарнирно-консольных балок

Контрольные вопросы

Почему недопустимы системы, близкие к мгновенно изменяемым?

Для чего проводится кинематический анализ систем?

Как проверить статическую определимость и геометрическую неизменяемость многопролетной статически определимой балки?

2. Расчёт сооружений на подвижную нагрузку

При расчёте сооружения на подвижную нагрузку: движущийся поезд, автомобиль – пользуются линиями влияния (лв).

Линия влияния – это график, показывающий закон изменения того или иного усилия: реакции, момента, поперечной силы – в определённом или фиксированном сечении сооружения при перемещении по его длине груза F=1.

Ордината линии влияния показывает величину усилия, для которого построена ЛВ, когда груз F=1 стоит над этой ординатой на сооружении.

Ординаты линий влияния R и Q безразмерны, а линии влияния М выражаются в метрах.

Сравнение линий влияния и эпюр какого-либо усилия J приведены в табл. 2.1.

Таблица 2.1

Сравнение линии влияния и эпюр

Для расчета балок первым делом необходимо определить усилия, возникающие в конструкциях. В данном разделе показано, как находить усилия, опорные реакции, прогибы и углы поворота в различных изгибаемых конструкциях. Для самых распространенных из них вы можете воспользоваться онлайн расчетом. Для редких — приведены все формулы определения необходимых значений.

Онлайн расчет балки на двух опорах (калькулятор).

Оранжевые ячейки — максимальные значения.

Онлайн расчет консольной балки (калькулятор).

Приведен расчет на момент, прогиб и опорные реакции от сосредоточенной и распределнной силы.

Синие ячейки — ввод данных. (Белые ячейки — ввод координаты для определения промежуточного итога).

Зеленые ячейки — расчетные, промежуточный итог.

Оранжевые ячейки — максимальные значения.

Расчет однопролетной балки на двух шарнирных опорах.

Рис.1 Расчет балки на двух

Представлены расчетные схемы, различные виды действующих нагрузок, эпюры сил, отображающие характер изменения касательных напряжений, эпюры изгибающих моментов, отображающие характер изменения нормальных напряжений, возникающих в поперечном сечении балки, а также формулы для определения опорных реакций, действующего изгибающего момента, максимального изгибающего момента, формулы для определения прогиба балки на расстоянии х от начала балки и формулы для определения максимального прогиба балки, а также формулы для определения тангенса угла поворота поперечного сечения на опорах и на концах — для консольных балок. Классификация производилась не по действующим нагрузкам, а по виду опор балки. В данном разделе представлены статически определимые балки. Ось х , относительно которой производятся расчеты изгибающего момента и прогиба, соответствует продольной оси, проходящей через центр тяжести поперечных сечений балки. Значение момента инерции I следует определять относительно оси z . Если в таблицах отсутствует формула для определения прогиба на каком-то из участков балки (из-за чрезмерной длины формулы), то опять же ее можно вывести, дважды должным образом проинтегрировав уравнение изгибающего момента, разделив результат на EI и добавив к этому результат интегрирования угла поворота. В общем виде уравнение для определения углов поворота выглядит так: θ х = — θ A + Мх/EI + Ax 2 /2EI — qx 3 /6ЕI например, для шарнирной балки, к которой приложена сосредоточенная нагрузка (таблица 1, №1.1, момент и распределенная нагрузка осутствуют) на участке от начала балки до точки приложения силы (0 θ х = — θ A + Ax 2 /2EI = — Ql 2 /16EI + Qx 2 /4EI = Q(4x 2 — l 2)/16EI Соответственно в общем виде уравнение для определения прогиба выглядит так: f х = — θ A x + Мх 2 /2EI + Ax 3 /6EI — qx 4 /24ЕI для той же шарнирной балки на участке от начала балки до точки приложения силы (0 f х = — θ A x + Ax 3 /6EI = — Ql 2 x/16EI + Qx 3 /12EI = Qx(4x 2 — 3l 2)/48EI На участке от точки приложения силы до конца балки (l/2 f х = — θ A x + Ax 3 /6EI — Q(x — l/2) 3 /6EI Эпюры углов поворота и прогибов поперечного сечения по длине балки не приводятся. Если в формуле прогиба есть знак минус, то это значит, что балка прогибается вниз (что в общем-то логично), а если быть более точным, то центр тяжести поперечного сечения смещается вниз по оси у . Представленные расчетные схемы позволяют рассчитать балку практически при любом возможном виде нагрузки. Если на балку действует несколько различных нагрузок, то можно производить отдельный расчет для каждой схемы загружения, а затем полученные результаты сложить (с учетом знаков). Это правило называется принципом суперпозиции и в некоторых случаях значительно упрощает общий расчет, а также экономит уйму времени на поиск в сети подходящей расчетной схемы. 1. БАЛКА НА ДВУХ ШАРНИРНЫХ ОПОРАХ 2. КОНСОЛЬНАЯ БАЛКА 3. БАЛКА НА ШАРНИРНЫХ ОПОРАХ С КОНСОЛЯМИ Расчетные схемы для статически неопределимых балок .

Расчёт балки бесплатно онлайн

Добро пожаловать! Данный онлайн-калькулятор предназначен для расчёта балки и позволит построить эпюры внутренних силовых факторов (изгибающих моментов, поперечных и осевых или продольных сил), рассчитать реакции в опорах. В итоге формируется отчёт с готовым решением. Удачи! 12

Операции Объекты В данном расчёте не задано ни одного закрепления или нагрузки. Для задания нагрузки и закреплений балки перейдите в раздел «Операции»

Балки — поддерживаются с обеих сторон

Напряжение в изгибающейся балке можно выразить как

σ = y M / I (1)

, где

σ = напряжение (Па (Н / м ^{) 2} ), Н / мм ² , psi)

y = расстояние до точки от нейтральной оси (м, мм, дюйм)

M = изгибающий момент (Нм, фунт-дюйм)

I = момент инерции (м ⁴ , мм ⁴ , в ⁴ )

Калькулятор ниже можно использовать для расчета максимального напряжения и прогиба балок с одной одиночной или равномерно распределенной нагрузкой.

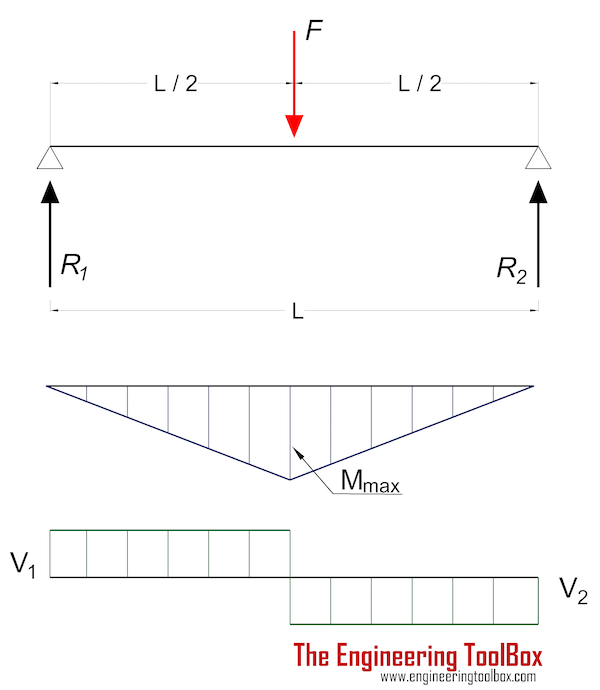
Балка, поддерживаемая на обоих концах — равномерная непрерывная распределенная нагрузка

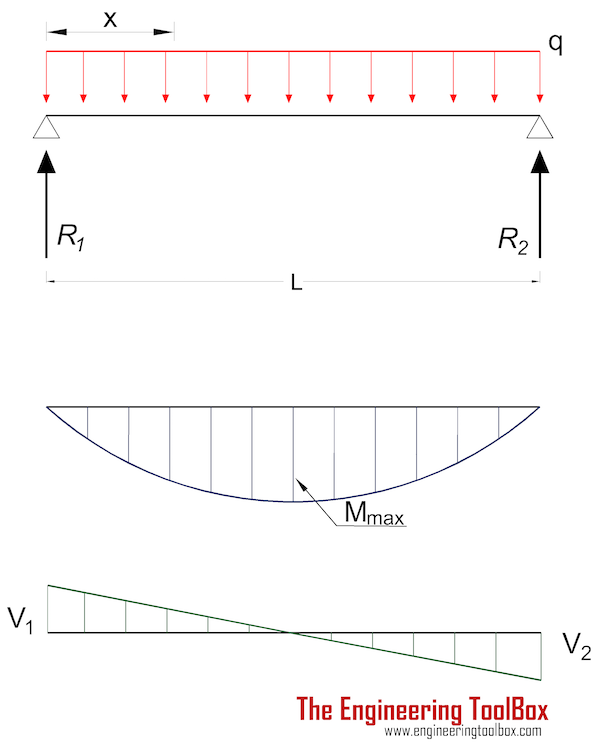
Момент в балке с равномерной нагрузкой, поддерживаемой на обоих концах в положении x, может быть выражен как

M _x = qx (L — x) / 2 (2)

где

M _x = момент в положении x (Нм, фунт дюйм)

x = расстояние от конца (м, мм, дюйм)

Максимум Момент находится в центре балки на расстоянии L / 2 и может быть выражен как

M _max = q L ² /8 (2a)

, где

M _max = максимальный момент ( Нм, фунт-дюйм)

q = равномерная нагрузка на единицу длины балки (Н / м, Н / мм, фунт / дюйм)

9000 2 L = длина балки (м, мм, дюйм)

Максимальное напряжение

Уравнения 1 и 2a могут быть объединены для выражения максимального напряжения в балке с равномерным нагрузка, поддерживаемая с обоих концов на расстоянии L / 2, как

σ _max = y _max q L ² / (8 I) (2b)

где

σ _max = максимальное напряжение (Па (Н / м ² ), Н / мм ² , psi)

y _max = расстояние до крайней точки от нейтральной оси (м, мм, дюйм)

• 1 Н / м ² = 1×10 ^-6 Н / мм ² = 1 Па = 1.4504×10 ^-4 фунтов на кв. Дюйм
• 1 фунт / дюйм (фунт / дюйм ² ) = 144 фунта на квадратный дюйм (фунт _на / фут ² ) = 6 894,8 Па (Н / м ² ) = 6,895×10 ^{— 3} Н / мм ²

Максимальный прогиб :

δ _max = 5 q L ⁴ / (384 EI) (2c)

где

δ _макс = максимальный прогиб (м, мм, дюйм)

E = Модуль упругости (Па (Н / м ² ), Н / мм ² , psi)

Прогиб в позиции x:

δ _x = qx ( L ³ — 2 L x ² + x ³ ) / (24 EI) (2d)

Примечание! — прогиб часто является ограничивающим фактором при проектировании балки.Для некоторых применений балки должны быть прочнее, чем требуется при максимальных нагрузках, чтобы избежать недопустимого прогиба.

Силы, действующие на концы:

R ₁ = R ₂

= q L / 2 (2e)

где

R = сила реакции (Н, фунт)

Пример — балка с равномерной нагрузкой, метрические единицы

Балка UB 305 x 127 x 42 длиной 5000 мм несет равномерную нагрузку 6 Н / мм .Момент инерции балки составляет 8196 см ⁴ (81960000 мм ⁴ ) , а модуль упругости стали, используемой в балке, составляет 200 ГПа (200000 Н / мм ² ) . Высота балки 300 мм (расстояние от крайней точки до нейтральной оси 150 мм ).

Максимальное напряжение в балке можно рассчитать

σ _max = (150 мм) (6 Н / мм) (5000 мм) ² / (8 (81960000 мм ⁴ ))

= 34.3 Н / мм ²

= 34,3 10 ⁶ Н / м ² (Па)

= 34,3 МПа

Максимальный прогиб балки можно рассчитать

δ _макс = 5 (6 Н / мм) (5000 мм) ⁴ / (( 200000 Н / мм) ² ) ( 81960000 мм ⁴ ) 384)

= 2,98 мм

Расчет балки с равномерной нагрузкой — метрические единицы

• 1 мм ⁴ = 10 ^-4 см ⁴ = 10 ^-12 м ⁴
• 1 см ⁴ = 10 ^-8 м = 10 ⁴ мм
• 1 дюйм ⁴ = 4.16×10 ⁵ мм ⁴ = 41,6 см ⁴
• 1 Н / мм ² = 10 ⁶ Н / м ² (Па)

Расчет балок с равномерной нагрузкой — Британские единицы

Пример — балка с равномерной нагрузкой, британские единицы

Максимальное напряжение в стальной широкополочной балке W 12 x 35 дюймов, длина 100 дюймов, длина , момент инерции 285 дюймов, ⁴ , модуль упругости 2

00 фунтов на квадратный дюйм , при равномерной нагрузке 100 фунтов / дюйм можно рассчитать как

σ _макс = y _макс q L ² / (8 I)

= (6.25 дюймов (100 фунтов / дюйм) (100 дюймов) ² / (8 (285 дюймов ⁴ ))

= 2741 (фунт / дюйм ² , psi)

Максимальный прогиб может рассчитывается как

δ _max = 5 q L ⁴ / (EI 384)

= 5 (100 фунтов / дюйм) (100 дюймов) ⁴ / ((2

00 фунтов / дюйм ² ) (285 дюймов ⁴ ) 384)

= 0,016 дюйма

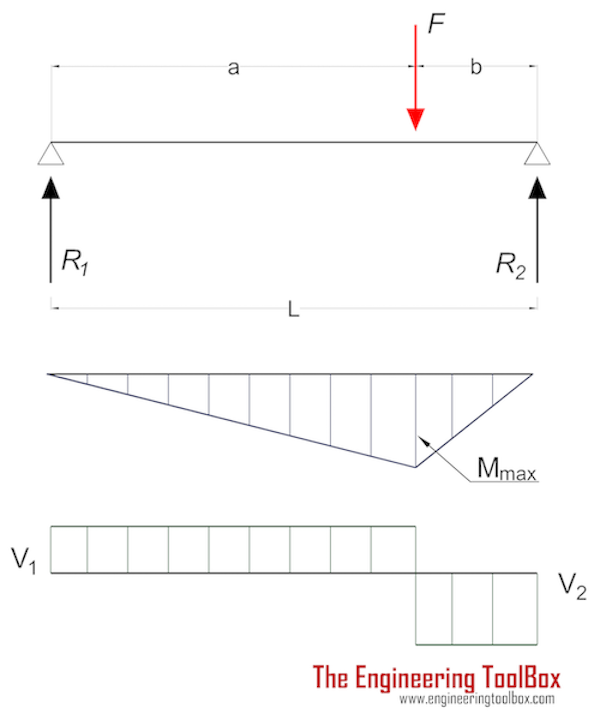
Балка, поддерживаемая на обоих концах — нагрузка в центре

Максимальный момент в балке с центральной нагрузкой, поддерживаемой с обеих сторон концов:

M _max = FL / 4 (3a)

Максимальное напряжение

Максимальное напряжение в балке с одноцентровой нагрузкой, поддерживаемой с обоих концов:

σ _max = y _max FL / (4 I) ( 3b)

где

F = нагрузка (Н, фунт)

Максимальный прогиб может быть выражен как

δ _max = FL ³ / (48 EI) (3c)

Силы, действующие на концы:

R ₁ = R ₂

= F / 2 (3d)

Расчет балки с одним центром нагрузки — метрические единицы

Расчет балки с одним центром нагрузки — Имперские единицы

Пример — Балка с одинарной центральной нагрузкой

Максимальное напряжение в стальной широкополочной балке W 12 x 35 дюймов, длина 100 дюймов, длина , момент инерции 285 дюймов, ⁴ , модуль упругости эластичность 2

00 psi , с центральной нагрузкой 10000 фунтов можно рассчитать как

σ _max = y _max FL / (4 I)

= (6.25 дюймов) (10000 фунтов) (100 дюймов) / (4 (285 дюймов ⁴ ))

= 5482 (фунт / дюйм ² , фунт / кв. Дюйм)

Максимальный прогиб можно рассчитать как

δ _max = FL ³ / EI 48

= (10000 фунтов / дюйм) (100 дюймов) ³ / ((2

00 фунтов / дюйм ² ) (285 дюймов ⁴ ) 48 )

= 0,025 дюйма

Некоторые типичные пределы отклонения по вертикали

• Полное отклонение: пролет / 250
• Прогиб при динамической нагрузке: пролет / 360
• консоли: пролет / 180
• Балки деревянных перекрытий в домашних условиях: пролет / 330 (макс. 14 мм)
• хрупкие элементы: пролет / 500
• подкрановые балки: пролет / 600

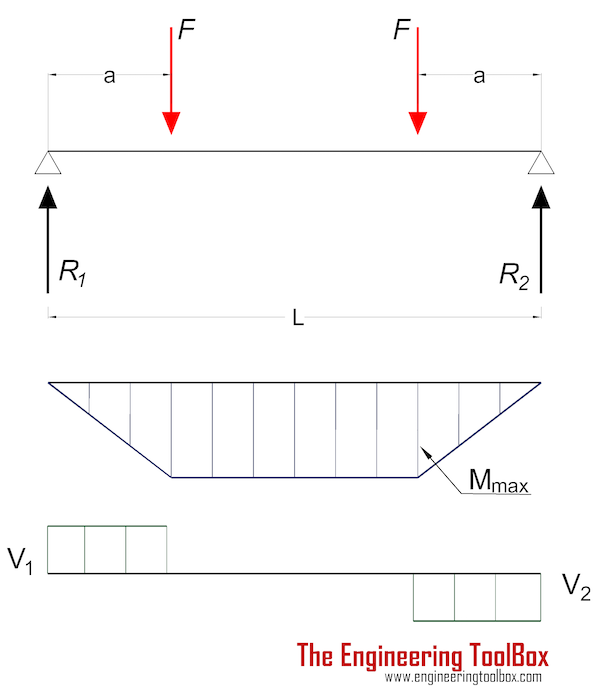
Балка, поддерживаемая на обоих концах — эксцентричная нагрузка

Максимальный момент в балке с одинарной эксцентричной нагрузкой при точка нагрузки:

M _{макс.9 0050 = F ab / L (4a)}

Максимальное напряжение

Максимальное напряжение в балке с одноцентровой нагрузкой, поддерживаемой с обоих концов:

σ _max = y _max F ab / (LI) (4b)

Максимальный прогиб в точке нагрузки может быть выражен как

δ _F = F a ² b ² / (3 EIL) (4c)

Силы, действующие на концы:

R ₁ = F b / L (4d)

R ₂ = F a / L (4e)

Балка, поддерживаемая на обоих концах — две эксцентрические нагрузки

Максимальный момент (между нагрузками) в балке с двумя эксцентрическими нагрузками:

M _max = F a (5a)

Максимальное напряжение

Максимальное напряжение в балке с двумя эксцентрическими нагрузками, поддерживаемыми на обоих концах:

σ _max = y _max F a / I (5b)

Максимум прогиб в точке нагрузки можно выразить как

δ _F = F a (3L ² — 4 a ² ) / (24 EI) (5c)

Силы, действующие на концы:

R ₁ = R ₂

= F (5d)

Вставьте балки в свою модель Sketchup с помощью Engineering ToolBox Sketchup Extension

Балка поддерживается на обоих концах — трехточечная нагрузка

Максимальный момент (между нагрузками) в балке с тремя точечными нагрузками: 9000 3

M _max = FL / 2 (6a)

Максимальное напряжение

Максимальное напряжение в балке с тремя точечными нагрузками, поддерживаемыми с обоих концов:

σ _max = y _max FL / (2 I) (6b)

Максимальный прогиб в центре балки можно выразить как

δ _F = FL ³ / (20.22 E I) (6c)

Силы, действующие на концы:

R ₁ = R ₂

= 1,5 F (6d)

.

Балки — фиксированные на обоих концах

Балки, фиксированные на обоих концах — одноточечная нагрузка

Изгибающий момент

M _A = — F ab ² / L ² (1a)

где

M _A = момент на неподвижном конце A (Нм, фунт _f футов)

F = нагрузка (Н, фунт _f )

M _B = — F a ² b / L ² (1b)

где

M _B = момент на неподвижном конце B (Нм, фунт _f футов)

M _F = 2 F a ² b ² / L ³ (1c)

где

M _F = момент при точечной нагрузке (Нм, фунт _f футов)

Прогиб

δ _F = F a ³ b ³ / (3 L ³ EI) (1d)

где

δ _F = прогиб при точечной нагрузке (м, фут)

E = Модуль упругости (Па (Н / м ² ), Н / мм ² , psi)

I = Момент площади инерции (м ⁴ , мм ⁴ , дюйм ⁴ )

Реакции опоры

R _A = F (3 a + b) b ² / L ³ (1f)

где

R _A = сила опоры на неподвижном конце A (Н, фунт _f )

R _B = F (a + 3 b) a ² / л ³ (1g)

, где

R _B = сила опоры на фиксированном конце B (Н, фунт _f )

Балка, закрепленная на обоих концах — равномерная непрерывная распределенная нагрузка

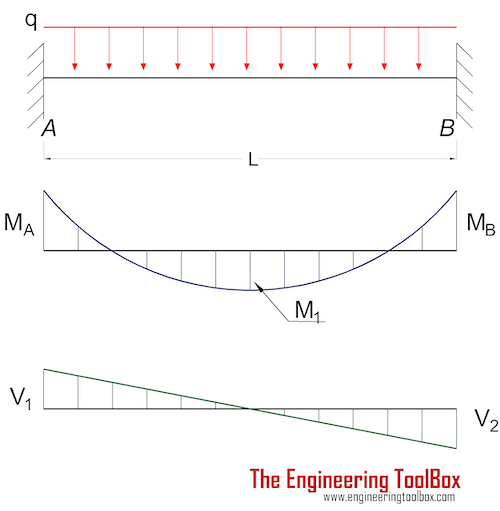Изгибающий момент

M _A = M _B

= — q L ² /12 (2a)

где

M = моменты на неподвижных концах (Нм, фунт _f фут)

q = равномерная нагрузка (Н / м, фунт _f / фут)

M ₁ = q L ² /24 (2b)

где

M ₁ = момент в центре (Нм, фунт _f футов)

Прогиб

δ _max = q L ⁴ / (384 EI) (2c)
9 0016

, где

δ _max = максимальный прогиб в центре (м, фут)

E = Модуль упругости (Па (Н / м ² ), Н / мм ^{) 2} , psi)

I = Момент инерции площади (м ⁴ , мм ⁴ , дюйм ⁴ )

Реакции опоры

R _A = R _B

= q L / 2 (2d)

, где

R = опорные силы на фиксированных концах (Н, фунт _f )

Балка, закрепленная на обеих Концы — равномерно уменьшающаяся распределенная нагрузка

Изгибающий момент

M _A = — q L ² /20 (3a)

где

M 90 009 A = моменты на неподвижном конце A (Нм, фунт _f фут)

q = равномерная падающая нагрузка (Н / м, фунт _f / фут)

M _B = — q L ² /30 (3b)

где

M _B = моменты на неподвижном конце B (Нм, фунт _f футов)

M ₁ = q L ² /46.6 (3c)

где

M ₁ = момент при x = 0,475 L (Нм, фунт _f футов)

Прогиб

δ _max = q L ⁴ / (764 EI) (3d)

где

δ _max = максимальный прогиб при x = 0,475 L (м, фут)

E = Модуль упругости (Па (Н / м ² ), Н / мм ² , psi)

I = Момент инерции площади (м ⁴ , мм ⁴ , дюйм ⁴ )

δ _1/2 = q L ⁴ / (768 EI) (3e)

где

δ _1/2 = прогиб при x = 0.5 л (м, фут)

Реакции опоры

R _A = 7 q L / 20 (3f)

где

R _A = сила опоры на неподвижном конце A (Н, фунт _f )

R _B = 3 q L / 20 (3g)

где

R _B = усилие опоры на неподвижном конце B (Н, фунт _f )

Балка, закрепленная на обоих концах — частично равномерная непрерывная распределенная нагрузка

Изгибающий момент

M _A = — (qa ² /6) (3-4 a / l + 1.5 (a / L) ² ) (4a)

где

M _A = момент на неподвижном конце A (Нм, фунт _f футов)

q = частично однородный нагрузка (Н / м, фунт _f / фут)

M _B = — (qa ² /3) (a / L — 0,75 (a / L) ² ) (4b)

, где

M _B = момент на неподвижном конце B (Нм, фунт _f футов)

Реакции опоры

R _A = qa (L — 0.5 a) / L — (M _A — M _B ) / L (4c)

где

R _A = сила опоры на неподвижном конце A (Н, фунт _f )

R _B = qa ² / (2 л) + (M _A — M _B ) / L (4d)

где

R _B = опорная сила на неподвижном конце B (Н, фунт _f )

.

Безразмерное аналитическое решение и новая формула расчета продольного изгиба двутавровых балок при линейном распределенном моменте с помощью теории линейной устойчивости

• Журналы
• Публикация с нами
• Партнерские отношения с издателями
• О нас

Blog15

Проблемы инженерии + Меню журнала PDF

Обзор журнала

Для авторов Для рецензентов Для редакторов Содержание

Специальные выпуски

ОтправитьМатематические проблемы в инженерии / 2017 / Статья Разделы статей

На этой странице

АннотацияВведениеВыводыКонфликт интересов БлагодарностиСсылкиАвторское право

Research Ar

.