Калькулятор расчёта площади комнаты, расчет площади пола и потолка
Приведу пример расчета пола или потолка комнаты (кухни) в квадратных метрах.
Формула расчета простая, S = a*b, где S — площадь, а и b — соответственно, длина и ширина комнаты.
В нашем примере (рисунка с обмерами) вместо маленьких букв длина — А и ширина — Б., и противоположенных стен — Г и В.
Чтобы рассчитать площадь комнаты по полу:
— если у нас длина комнаты 5 метра, а ширина 3 метров, тогда нам надо ( 5*3 = 15 кв.м.), в итоге получаем 15 кв.м. по полу
Воспользуйтесь нашим Калькулятором, чтобы расчитать площадь пола или потолка
Если вы не хотите в ручную рассчитывать площадь пола или вы, что то не поняли при описание расчетов, то вы можете воспользоваться нашим калькулятором и рассчитать площадь пола или потолка автоматически.
Для расчёта необходимо измерить в метрах длину, ширину комнаты и внести данные по порядку заполнив форму и вы автоматически получите расчет площади пола или потолка в квадратных метрах.
Калькулятор расчёта площади пола
Примечание:
Обращаем ваше внимание, что измерения необходимо проводить в метрах. Т.е. если вы получили длину комнаты 964 сантиметров, то в поля формы необходимо ввести значение 9.64. Обратите внимание, что дробные числа нужно вводить с точкой, а не с запятой!
Т.е. 2,6 — неправильно, 2.6 — правильно
Калькулятор рассчитывает не только площадь пола или потолка, данный калькулятор можно также использовать для расчёта площади любых других прямоугольных объектов у которых есть длина и ширина. В этом случае вместо ширины и длины комнаты вам необходимо подставить значения ширины и длины этих самых объектов (окна, двери и т. д.,) к примеру таких как площадь окон и дверей.
д.,) к примеру таких как площадь окон и дверей.
К примеру как можно проверить и расчитать в ручную
— если у нас размеры окна ширина 1,6 метров, а высота 1,5 метров.
— а двери ширина 0,8 метров, а высота 2,05 метров.
Окно: (1,6*1,5)= 2,4 кв.м., в итоге окно получаем 2,4 кв.м.,
Двери: (0,8*2,05)= 1,64 кв.м, в итоге двери получаем 1,64 кв.м.,
Чтобы рассчитать площадь комнаты по стенам: воспользуйтесь нашим Калькулятором, чтобы расчитать площадь стен
Источник: remont-otdelka-m.ru
Конвертер площади • Популярные конвертеры единиц • Компактный калькулятор • Онлайн-конвертеры единиц измерения
Конвертер длины и расстоянияКонвертер массыКонвертер мер объема сыпучих продуктов и продуктов питанияКонвертер площадиКонвертер объема и единиц измерения в кулинарных рецептахКонвертер температурыКонвертер давления, механического напряжения, модуля ЮнгаКонвертер энергии и работыКонвертер мощностиКонвертер силыКонвертер времениКонвертер линейной скоростиПлоский уголКонвертер тепловой эффективности и топливной экономичностиКонвертер чисел в различных системах счисления. Конвертер единиц измерения количества информацииКурсы валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер вращающего моментаКонвертер удельной теплоты сгорания (по массе)Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему)Конвертер разности температурКонвертер коэффициента теплового расширенияКонвертер термического сопротивленияКонвертер удельной теплопроводностиКонвертер удельной теплоёмкостиКонвертер энергетической экспозиции и мощности теплового излученияКонвертер плотности теплового потокаКонвертер коэффициента теплоотдачиКонвертер объёмного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер плотности потока массыКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкостиКонвертер кинематической вязкостиКонвертер поверхностного натяженияКонвертер паропроницаемостиКонвертер плотности потока водяного параКонвертер уровня звукаКонвертер чувствительности микрофоновКонвертер уровня звукового давления (SPL)Конвертер уровня звукового давления с возможностью выбора опорного давленияКонвертер яркостиКонвертер силы светаКонвертер освещённостиКонвертер разрешения в компьютерной графикеКонвертер частоты и длины волныОптическая сила в диоптриях и фокусное расстояниеОптическая сила в диоптриях и увеличение линзы (×)Конвертер электрического зарядаКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаКонвертер объемной плотности зарядаКонвертер электрического токаКонвертер линейной плотности токаКонвертер поверхностной плотности токаКонвертер напряжённости электрического поляКонвертер электростатического потенциала и напряженияКонвертер электрического сопротивленияКонвертер удельного электрического сопротивленияКонвертер электрической проводимостиКонвертер удельной электрической проводимостиЭлектрическая емкостьКонвертер индуктивностиКонвертер реактивной мощностиКонвертер Американского калибра проводовУровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др.
Конвертер единиц измерения количества информацииКурсы валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер вращающего моментаКонвертер удельной теплоты сгорания (по массе)Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему)Конвертер разности температурКонвертер коэффициента теплового расширенияКонвертер термического сопротивленияКонвертер удельной теплопроводностиКонвертер удельной теплоёмкостиКонвертер энергетической экспозиции и мощности теплового излученияКонвертер плотности теплового потокаКонвертер коэффициента теплоотдачиКонвертер объёмного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер плотности потока массыКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкостиКонвертер кинематической вязкостиКонвертер поверхностного натяженияКонвертер паропроницаемостиКонвертер плотности потока водяного параКонвертер уровня звукаКонвертер чувствительности микрофоновКонвертер уровня звукового давления (SPL)Конвертер уровня звукового давления с возможностью выбора опорного давленияКонвертер яркостиКонвертер силы светаКонвертер освещённостиКонвертер разрешения в компьютерной графикеКонвертер частоты и длины волныОптическая сила в диоптриях и фокусное расстояниеОптическая сила в диоптриях и увеличение линзы (×)Конвертер электрического зарядаКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаКонвертер объемной плотности зарядаКонвертер электрического токаКонвертер линейной плотности токаКонвертер поверхностной плотности токаКонвертер напряжённости электрического поляКонвертер электростатического потенциала и напряженияКонвертер электрического сопротивленияКонвертер удельного электрического сопротивленияКонвертер электрической проводимостиКонвертер удельной электрической проводимостиЭлектрическая емкостьКонвертер индуктивностиКонвертер реактивной мощностиКонвертер Американского калибра проводовУровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др. единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева
единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева
В Мьянме и в Северной Америке для измерения площади земельных владений используют акры
Общие сведения
В ряде Европейских стран и в Индонезии площадь земельных участков измеряют в арах
Площадь — это величина геометрической фигуры в двумерном пространстве. Она используется в математике, медицине, инженерных и других науках, например, в вычислении поперечного сечения клеток, атомов, или труб, таких как кровеносные сосуды или водопроводные трубы. В географии площадь используются для сравнения размеров городов, озер, стран и других географических объектов. При расчетах плотности населения также используется площадь. Плотность населения определяется как количество людей на единицу площади.
В географии площадь используются для сравнения размеров городов, озер, стран и других географических объектов. При расчетах плотности населения также используется площадь. Плотность населения определяется как количество людей на единицу площади.
Единицы
Квадратные Метры
Площадь измеряется в системе СИ в квадратных метрах. Один квадратный метр — площадь квадрата, со стороной в один метр.
Единичный квадрат
Единичный квадрат это квадрат со сторонами в одну единицу. Площадь единичного квадрата тоже равна единице. В прямоугольной системе координат этот квадрат находится в координатах (0,0), (0,1), (1,0) и (1,1). На комплексной плоскости координаты — 0, 1, i и i+1, где i — мнимое число.
Ар
Ар или сотка, как мера площади, используется в странах СНГ, Индонезии и некоторых других странах Европы, для измерения небольших городских объектов таких как парки, когда гектар слишком велик. Один ар равен 100 квадратным метрам. В некоторых странах эта единица называется иначе.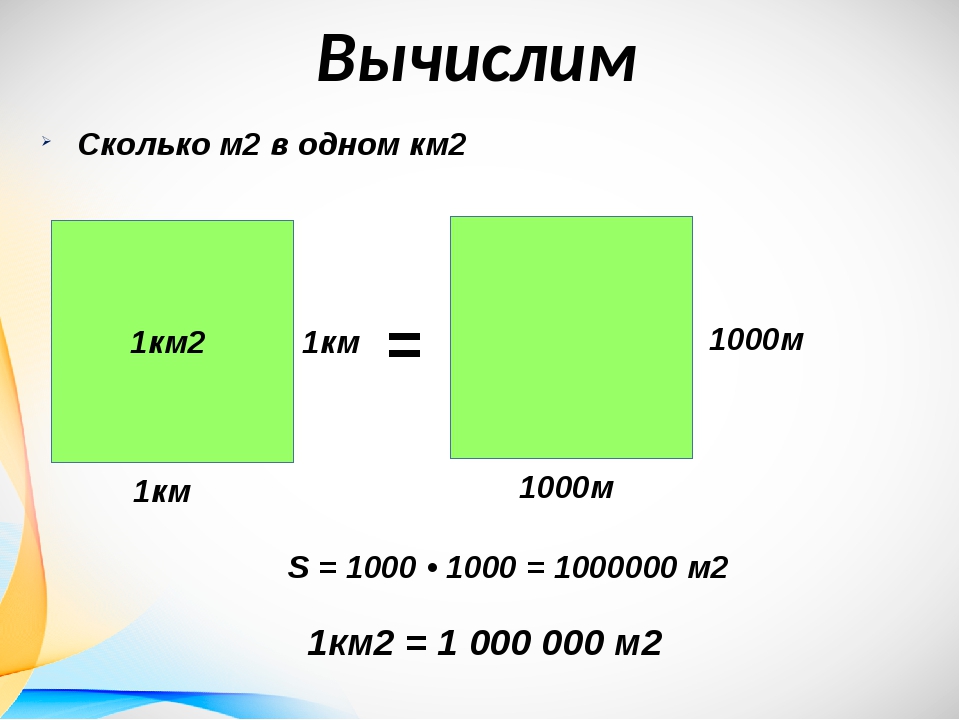
Гектар
В гектарах измеряют недвижимость, особенно земельные участки. Один гектар равен 10 000 квадратных метров. Он используется со времен Французской революции, и применяется в Европейском Союзе и некоторых других регионах. Так же как и ар, в некоторых странах гектар называется иначе.
В южной части провинции Онтарио, Канада
Акр
В Северной Америке и Бирме площадь измеряется в акрах. Гектары там не используются. Один акр равен 4046,86 квадратным метрам. Изначально акр определялся как площадь, которую за один день мог вспахать крестьянин с упряжкой из двух волов.
Барн
Барны используются в ядерной физике для измерения поперечного сечения атомов. Один барн равен 10⁻²⁸ квадратным метрам. Барн не является единицей в системе СИ, но принят к использованию в этой системе. Один барн приблизительно равен площади поперечного сечения ядра урана, которое физики в шутку называли «огромным, как амбар». Амбар по-английски «barn» (произносится барн) и из шутки физиков это слово стало названием единицы площади. Эта единица возникла во время Второй мировой войны, и понравилась ученым, потому что ее название можно было использовать как кодовое в переписке и телефонных разговорах в рамках Манхэттенского проекта.
Эта единица возникла во время Второй мировой войны, и понравилась ученым, потому что ее название можно было использовать как кодовое в переписке и телефонных разговорах в рамках Манхэттенского проекта.
Расчет площади
Площадь простейших геометрических фигур находят, сравнивая их с квадратом известной площади. Это удобно тем, что площадь квадрата легко вычислить. Некоторые формулы вычисления площади геометрических фигур, приведенные ниже, получены именно таким путем. Также для вычисления площади, особенно многоугольника, фигуру делят на треугольники, вычисляют площадь каждого треугольника по формуле, а потом складывают. Площадь более сложных фигур вычисляют с помощью математического анализа.
Формулы для вычисления площади
- Квадрат: сторона в квадрате.
- Прямоугольник: произведение сторон.
- Треугольник (известна сторона и высота): произведение стороны и высоты (расстояния от этой стороны до ребра), деленное пополам. Формула: A = ½ah, где A — площадь, a — сторона, и h — высота.

- Треугольник (известны две стороны и угол между ними): произведение сторон и синуса угла между ними, деленное пополам. Формула: A = ½ab sin(α), где A — площадь, a и b — стороны, и α — угол между ними.
- Равносторонний треугольник: сторона, в квадрате, деленная на 4 и умноженная на квадратный корень из трех.
- Параллелограмм: произведение стороны и высоты, измеряемой от этой стороны, до противоположной.
- Трапеция: сумма двух параллельных сторон, умноженная на высоту, и деленная на два. Высота измеряется между этими двумя сторонами.
- Круг: произведение квадрата радиуса и π.
- Эллипс: произведение полуосей и π.
Площадь поверхности Луны равна приблизительно 3,793 x 10⁷ квадратным километрам
Вычисление площади поверхности
Найти площадь поверхности простых объемных фигур, таких как призмы, можно по развертке этой фигуры на плоскости. Развертку шара получить таким образом невозможно. Площадь поверхности шара находят с помощью формулы, умножая квадрат радиуса на 4π. Из этой формулы следует, что площадь круга в четыре раза меньше площади поверхности шара с таким же радиусом.
Площадь поверхности шара находят с помощью формулы, умножая квадрат радиуса на 4π. Из этой формулы следует, что площадь круга в четыре раза меньше площади поверхности шара с таким же радиусом.
Площади поверхности некоторых астрономических объектов: Солнце — 6,088 x 10¹² квадратных километров; Земля — 5,1 x 10⁸; таким образом, площадь поверхности Земли примерно в 12 раз меньше площади поверхности Солнца. Площадь поверхности Луны приблизительно равна 3,793 x 10⁷ квадратных километров, что примерно в 13 раз меньше площади поверхности Земли.
Планиметр
Площадь также можно вычислить с помощью специального прибора — планиметра. Существуют несколько видов этого прибора, например полярный и линейный. Также, планиметры бывают аналоговыми и цифровыми. В дополнение к другим функциям, в цифровые планиметры можно вводить масштаб, что облегчает измерение объектов на карте. Планиметр измеряет расстояние, пройденное по периметру измеряемого объекта, а также направление. Расстояние, пройденное планиметром параллельно его оси, не измеряется. Эти устройства используются в медицине, биологии, технике, и сельском хозяйстве.
Эти устройства используются в медицине, биологии, технике, и сельском хозяйстве.
Интересные факты о площади
Теорема о свойствах площадей
Согласно изопериметрической теореме, из всех фигур с одинаковым периметром, самая большая площадь у круга. Если, наоборот, сравнить фигуры с одинаковой площадью, то у круга самый маленький периметр. Периметр — это сумма длин сторон геометрической фигуры, или линия, которая обозначает границы этой фигуры.
Географические объекты с самой большой площадью
Вид на вечерний Нью-Йорк с 35-го этажа из окна гостиницы ONE UN New York Hotel
Страна: Россия, 17 098 242 квадратных километров, включая сушу и водное пространство. Вторая и третья по площади страны — это Канада и Китай.
Город: Нью-Йорк — это город с самой большой площадью в 8683 квадратных километров. Второй по площади город — Токио, занимающий 6993 квадратных километров. Третий — Чикаго, с площадью в 5498 квадратных километров.
Городская площадь: Самая большая площадь, занимающая 1 квадратный километр, находится в столице Индонезии Джакарте. Это площадь Медан Мердека. Вторая по величине площадь в 0,57 квадратного километра — Праса-дуз-Жирасойс в городе Палмас, в Бразилии. Третья по величине — площадь Тяньаньмэнь в Китае, 0,44 квадратного километра.
Это площадь Медан Мердека. Вторая по величине площадь в 0,57 квадратного километра — Праса-дуз-Жирасойс в городе Палмас, в Бразилии. Третья по величине — площадь Тяньаньмэнь в Китае, 0,44 квадратного километра.
Озеро: Географы спорят, является ли Каспийское море озером, но если это так, то это — самое большое озеро в мире с площадью 371 000 квадратных километров. Второе по площади озеро — озеро Верхнее в Северной Америке. Это одно из озер системы Великих озер; его площадь составляет 82 414 квадратных километров. Третье по площади — озеро Виктория в Африке. Оно занимает площадь 69 485 квадратных километров.
Список литературы
Автор статьи: Kateryna Yuri
Вы затрудняетесь в переводе единицы измерения с одного языка на другой? Коллеги готовы вам помочь. Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ.
Квадратный метр
Площадь представляет собой важную величину, которой часто оперируют владельцы земельных участков. Ее также используют фермеры, строители и многие другие. Что же представляет собой такая величина и как она рассчитывается? Сколько площади занимает квадратный метр и как его рассчитать?
Что же представляет собой такая величина и как она рассчитывается? Сколько площади занимает квадратный метр и как его рассчитать?
Определение
Площадь представляет собой двухмерную характеристику пространства, которая определяет размер геометрических фигур. Ее используют в медицине, математике, сельском хозяйстве, инженерии. В географии величину используется для определения размеров озер и стран, а также для сравнительной характеристики городов и различных местностей. Также при помощи площади определяется плотность населения на определенной территории. Сколько квадратных метров в 1 га? Чтобы это выяснить, следует разобраться с единицами измерения.
Единицы площади
Существует несколько основных единиц, которыми измеряется площадь. Они позволяют представить масштаб измеряемых территорий. Одной из самых распространенных величин является квадратный метр (м2). Он часто используется для оценивания площадей жилых, офисных и производственных помещений. Так, 1 кв. м равен участку плоскости, каждая сторона которого имеет длину 1 м. Чтобы понять,сколько квадратных сантиметров в квадратном метре, стоит познакомиться с единицами измерений.
Так, 1 кв. м равен участку плоскости, каждая сторона которого имеет длину 1 м. Чтобы понять,сколько квадратных сантиметров в квадратном метре, стоит познакомиться с единицами измерений.
Существуют такие величины:
- Единичный квадрат. Такая единица представляет собой квадрат, в которой стороны равны определенной единице. Единице равна и его площадь.
- Ар. Также его называют соткой. Используется для измерения достаточно больших объектов. Один ар равняется 100 кв. м.
- Гектар. Обычно гектары используются при оценивании недвижимости. Если перевести в квадратные метры, один гектар содержит в себе 10тыс. кв. м.
- Акр. Его значение равно 4046,86 кв. м. Произошла такая величина в результате нехитрых измерений. Раньше ей обозначалась площадь, которую способен вскопать крестьянин за день. При этом в его упряжке должно было находиться 2 вола.
- Барн. Эту величину используют физики-ядерщики. При помощи ее измеряется сечение атомов. Так, 1 барн равняется 10⁻²⁸ кв.
 м. Можно спросить – это сколько? Если после запятой вставить 28 нолей, и только потом единицу, получится наглядный ответ.
м. Можно спросить – это сколько? Если после запятой вставить 28 нолей, и только потом единицу, получится наглядный ответ.
Особой популярностью для решения повседневных задач пользуется квадратный метр. Такую величину стоит рассмотреть подробнее. Также полезно будет узнать, как определять размер территории при помощи нехитрых вычислений.
Определение площади
Чаще всего при помощи квадратного метра вычисляют площадь пола помещений, а также полей различного назначения. К примеру, можно измерить футбольное поле или комнату для проживания. Сделать это можно при помощи обычной рулетки или мерной ленты. Размер участка территории вычисляется достаточно просто – необходимо умножить долину измеренной территории на ее ширину.
Измерение площади
Чтобы измерить площадь определенной территории, стоит выбрать мерную ленту. Ее использование позволит сделать процесс измерения более простым и быстрым.При наличии рулетки или ленты, которая измеряет в дюймах стоит сначала провести все необходимые вычисления, а потом перевести дюймы в квадратные метры.
Особенности измерения участка пространства в кв. м:
- Определение длины измеряемой области. Выполняется процедура путем прокладывания измерительной ленты от одного угла квадрата или прямоугольника к другому. Длина – это большая из сторон.
- При длине большей, чем 1 м, стоит посчитать и сантиметры.
- Если объект представляет собой не квадрат и не прямоугольник, стоит либо разбить его на эти фигуры, либо воспользоваться методом расчета сложных фигур.
- При невозможности измерить длину 1 раз стоит делать это поэтапно. Необходимо разложить рулетку сделать необходимые отметки там, где она заканчивается. Повторять необходимо до тех пор, пока не будет измерена вся длина.
- После этого приступают к измерению ширины. Для этого рулетку кладут под углом 90 градусов к длине объекта. Полученное число, как и в случае с длиной, нужно записать.
После того как измерения проведены, необходимо перевести сантиметры в метры. Стоит помнить, что 1 см равен 0,1 м. Это означает, что если в результате измерений получились числа 4 м 35 см, при переводе в метры получится 4,35 м.
Это означает, что если в результате измерений получились числа 4 м 35 см, при переводе в метры получится 4,35 м.
После того как все полученные величины (длина и ширина) оказались в метрах, их необходимо перемножить. Результатом умножения окажется искомая площадь. К примеру, если длина получилась 3 м, а ширина – 2, путем несложного вычисления (3х2) можно получить количество кв. м. территории – 6. Также стоит знать, что в квадратном метре находится 10 000 кв. см.
Если чисел после запятой достаточно много, полученную цифру можно округлить. Если измерения были проведены не с точностью до миллиметра, полученный результат все равно окажется неточным.
Важно
Каждый раз, умножая различные числа, которые выражены в одинаковых единицах измерения, полученный результат должен также отображаться в них. К примеру, если длина и ширина были в сантиметрах, то и площадь будет в сантиметрах.
Периметр, площадь и объем
Данный материал содержит геометрические фигуры с измерениями. Приведённые измерения являются приблизительными и могут не совпадать с измерениями в реальной жизни.
Периметр геометрической фигуры
Периметр геометрической фигуры — это сумма всех её сторон. Чтобы вычислить периметр, нужно измерить каждую сторону и сложить результаты измерений.
Вычислим периметр следующей фигуры:
Это прямоугольник. Детальнее мы поговорим об этой фигуре позже. Сейчас просто вычислим периметр этого прямоугольника. Длина его равна 9 см, а ширина 4 см.
У прямоугольника противоположные стороны равны. Это видно на рисунке. Если длина равна 9 см, а ширина равна 4 см, то противоположные стороны будут равны 9 см и 4 см соответственно:
Найдём периметр. Для этого сложим все стороны.
P = 9 см + 4 см + 9 см + 4 см = 26 см.
Поскольку у прямоугольника противоположные стороны равны, нахождение периметра записывают короче — складывают длину и ширину, и умножают её на 2, что будет означать «повторить длину и ширину два раза»
P = 2 × (9 + 4) = 18 + 8 = 26 см.
Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, найдём периметр квадрата со стороной 5 см. Фразу
Чтобы вычислить периметр, сложим все стороны:
P = 5 см + 5 см + 5 см + 5 см = 20 см
Но поскольку все стороны равны, вычисление периметра можно записать в виде произведения. Сторона квадрата равна 5 см, и таких сторон 4. Тогда эту сторону, равную 5 см нужно повторить 4 раза
Тогда эту сторону, равную 5 см нужно повторить 4 раза
P = 5 см × 4 = 20 см
Площадь геометрической фигуры
Площадь геометрической фигуры — это число, которое характеризует размер данной фигуры.
Следует уточнить, что речь в данном случае идёт о площади на плоскости. Плоскостью в геометрии называют любую плоскую поверхность, например: лист бумаги, земельный участок, поверхность стола.
Площадь измеряется в квадратных единицах. Под квадратными единицами подразумевают квадраты, стороны которых равны единице. Например, 1 квадратный сантиметр, 1 квадратный метр или 1 квадратный километр.
Измерить площадь какой-нибудь фигуры означает выяснить сколько квадратных единиц содержится в данной фигуре.
Например, площадь следующего прямоугольника равна трём квадратным сантиметрам:
Это потому что в данном прямоугольнике содержится три квадрата, каждый из которых имеет сторону, равную одному сантиметру:
Справа представлен квадрат со стороной 1 см (он в данном случае является квадратной единицей). Если посмотреть сколько раз этот квадрат входит в прямоугольник, представленный слева, то обнаружим, что он входит в него три раза.
Если посмотреть сколько раз этот квадрат входит в прямоугольник, представленный слева, то обнаружим, что он входит в него три раза.
Следующий прямоугольник имеет площадь, равную шести квадратным сантиметрам:
Это потому что в данном прямоугольнике содержится шесть квадратов, каждый из которых имеет сторону, равную одному сантиметру:
Допустим, потребовалось измерить площадь следующей комнаты:
Определимся в каких квадратах будем измерять площадь. В данном случае площадь удобно измерить в квадратных метрах:
Итак, наша задача состоит в том, чтобы определить сколько таких квадратов со стороной 1 м содержится в исходной комнате. Заполним этим квадратом всю комнату:
Видим, что квадратный метр содержится в комнате 12 раз. Значит, площадь комнаты составляет 12 квадратных метров.
Площадь прямоугольника
В предыдущем примере мы вычислили площадь комнаты, последовательно проверив сколько раз в ней содержится квадрат, сторона которого равна одному метру. Площадь составила 12 квадратных метров.
Площадь составила 12 квадратных метров.
Комната представляла собой прямоугольник. Площадь прямоугольника можно вычислить перемножив его длину и ширину.
Чтобы вычислить площадь прямоугольника, нужно перемножить его длину и ширину.
Вернёмся к предыдущему примеру. Допустим, мы измерили длину комнаты рулеткой и оказалось, что длина составила 4 метра:
Теперь измерим ширину. Пусть она составила 3 метра:
Умножим длину (4 м) на ширину (3 м).
4 × 3 = 12
Как и в прошлый раз получаем двенадцать квадратных метров. Это объясняется тем, что измерив длину, мы тем самым узнаём сколько раз можно уложить в эту длину квадрат со стороной, равной одному метру. Уложим четыре квадрата в эту длину:
Затем мы определяем сколько раз можно повторить эту длину с уложенными квадратами. Это мы узнаём, измерив ширину прямоугольника:
Площадь квадрата
Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, на следующем рисунке представлен квадрат со стороной 3 см. Фраза «квадрат со стороной 3 см» означает, что все стороны равны 3 см
Например, на следующем рисунке представлен квадрат со стороной 3 см. Фраза «квадрат со стороной 3 см» означает, что все стороны равны 3 см
Площадь квадрата вычисляется таким же образом, как и площадь прямоугольника — длину умножают на ширину.
Вычислим площадь квадрата со стороной 3 см. Умножим длину 3 см на ширину 3 см
3 × 3 = 9
В данном случае требовалось узнать сколько квадратов со стороной 1 см содержится в исходном квадрате. В исходном квадрате содержится девять квадратов со стороной 1 см. Действительно, так оно и есть. Квадрат со стороной 1 см, входит в исходный квадрат девять раз:
Умножив длину на ширину, мы получили выражение 3 × 3, а это есть произведение двух одинаковых множителей, каждый из которых равен 3. Иными словами выражение 3 × 3 представляет собой вторую степень числа 3. А значит процесс вычисления площади квадрата можно записать в виде степени 32.
Поэтому вторую степень числа называют квадратом числа.
Обозначения
Площадь обозначается заглавной латинской буквой S (англ. Square — квадрат). Тогда площадь квадрата со стороной a см будет вычисляться по следующему правилу
S = a2
где a — длина стороны квадрата. Вторая степень указывает на то, что происходит перемножение двух одинаковых сомножителей, а именно длины и ширины. Ранее было сказано, что у квадрата все стороны равны, а значит равны длина и ширина квадрата, выраженные через букву a.
Если задача состоит в том, чтобы определить сколько квадратов стороной 1 см содержится в исходном квадрате, то в качестве единиц измерения площади нужно указывать см2. Это обозначение заменяет словосочетание «квадратный сантиметр».
Например, вычислим площадь квадрат со стороной 2 см.
Значит, квадрат со стороной 2 см, имеет площадь, равную четырём квадратным сантиметрам:
Если задача состоит в том, чтобы определить сколько квадратов со стороной 1 м содержится в исходном квадрате, то в качестве единиц измерения нужно указывать м2. Это обозначение заменяет словосочетание «квадратный метр».
Вычислим площадь квадрата со стороной 3 метра
Значит, квадрат со стороной 3 м, имеет площадь равную девяти квадратным метрам:
Аналогичные обозначения используются при вычислении площади прямоугольника. Но длина и ширина прямоугольника могут быть разными, поэтому они обозначаются через разные буквы, например a и b. Тогда площадь прямоугольника, длиной a и шириной b вычисляется по следующему правилу:
S = a × b
Как и в случае с квадратом, единицами измерения площади прямоугольника могут быть см2, м2, км2. Эти обозначения заменяют словосочетания «квадратный сантиметр», «квадратный метр», «квадратный километр» соответственно.
Эти обозначения заменяют словосочетания «квадратный сантиметр», «квадратный метр», «квадратный километр» соответственно.
Например, вычислим площадь прямоугольника, длиной 6 см и шириной 3 см
Значит, прямоугольник длиной 6 см и шириной 3 см имеет площадь, равную восемнадцати квадратным сантиметрам:
В качестве единицы измерения допускается использовать словосочетание «квадратных единиц». Например, запись S = 3 кв.ед означает, что площадь квадрата или прямоугольника равна трём квадратам, каждый из которых имеет единичную сторону (1 см, 1 м или 1 км).
Перевод единиц измерения площади
Единицы измерения площади можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:
Пример 1. Выразить 1 квадратный метр в квадратных сантиметрах.
1 квадратный метр это квадрат со стороной 1 м. То есть все четыре стороны имеют длину, равную одному метру.
Но 1 м = 100 см. Тогда все четыре стороны тоже имеют длину, равную 100 см
Тогда все четыре стороны тоже имеют длину, равную 100 см
Вычислим новую площадь этого квадрата. Умножим длину 100 см на ширину 100 см или возведём в квадрат число 100
S = 1002 = 10 000 см2
Получается, что на один квадратный метр приходится десять тысяч квадратных сантиметров.
1 м2 = 10 000 см2
Это позволяет в будущем умножить любое количество квадратных метров на 10 000 и получить площадь, выраженную в квадратных сантиметрах.
Чтобы перевести квадратные метры в квадратные сантиметры, нужно количество квадратных метров умножить на 10 000.
А чтобы перевести квадратные сантиметры в квадратные метры, нужно наоборот количество квадратных сантиметров разделить на 10 000.
Например, переведём 100 000 см2 в квадратные метры. Рассуждать в этом случае можно так: «если 10 000 см2 это один квадратный метр, то сколько раз 100 000 см2 будут содержать по 10 000 см2»
100 000 см2 : 10 000 см2 = 10 м2
Другие единицы измерения можно переводить таким же образом. Например, переведём 2 км2 в квадратные метры.
Например, переведём 2 км2 в квадратные метры.
Один квадратный километр это квадрат со стороной 1 км. То есть все четыре стороны имеют длину, равную одному километру. Но 1 км = 1000 м. Значит, все четыре стороны квадрата также равны 1000 м. Найдём новую площадь квадрата, выраженную в квадратных метрах. Для этого умножим длину 1000 м на ширину 1000 м или возведём в квадрат число 1000
S = 10002 = 1 000 000 м2
Получается, что на один квадратный километр приходится один миллион квадратных метров:
1 км2 = 1 000 000 м2
Это позволяет в будущем умножить любое количество квадратных километров на 1 000 000 и получить площадь, выраженную в квадратных метрах.
Чтобы перевести квадратные километры в квадратные метры, нужно количество квадратных километров умножить на 1 000 000.
Итак, вернёмся к нашей задаче. Требовалось перевести 2 км2 в квадратные метры. Умножим 2 км2 на 1 000 000
2 км2 × 1 000 000 = 2 000 000 м2
А чтобы перевести квадратные метры в квадратные километры, нужно наоборот количество квадратных метров разделить на 1 000 000.
Например, переведём 3 500 000 м2 в квадратные километры. Рассуждать в этом случае можно так: «если 1 000 000 м2 это один квадратный километр, то сколько раз 3 500 000 м2 будут содержать по 1 000 000 м2»
3 500 000 м2 : 1 000 000 м2 = 3,5 км2
Пример 2. Выразить 7 м2 в квадратных сантиметрах.
Умножим 7 м2 на 10 000
7 м2 = 7 м2 × 10 000 = 70 000 см2
Пример 3. Выразить 5 м2 13 см2 в квадратных сантиметрах.
5 м2 13 см2 = 5 м2 × 10 000 + 13 см2 = 50 013 см2
Пример 4. Выразить 550 000 см2 в квадратных метрах.
Узнаем сколько раз 550 000 см2 содержит по 10 000 см2. Для этого разделим 550 000 см2 на 10 000 см2
550 000 см2 : 10 000 см2 = 55 м2
Пример 5. Выразить 7 км2 в квадратных метрах.
Выразить 7 км2 в квадратных метрах.
Умножим 7 км2 на 1 000 000
7 км2 × 1 000 000 = 7 000 000 м2
Пример 6. Выразить 8 500 000 м2 в квадратных километрах.
Узнаем сколько раз 8 500 000 м2 содержит по 1 000 000 м2. Для этого разделим 8 500 000 м2 на 1 000 000 м2
8 500 000 м2 × 1 000 000 м2 = 8,5 км2
Единицы измерения площади земельных участков
Площади небольших земельных участков удобно измерять в квадратных метрах.
Площади более крупных земельных участков измеряются в арах и гектарах.
Ар (сокращённо: a) — это площадь равная ста квадратным метрам (100 м2). В виду частого распространения такой площади (100 м2) она стала использоваться, как отдельная единица измерения.
Например, если сказано что площадь какого-нибудь поля составляет 3 а, то нужно понимать, что это три квадрата площадью 100 м2 каждый, то есть:
3 а = 100 м2 × 3 = 300 м2
В народе ар часто называют соткой, поскольку ар равен квадрату, площадью 100 м2. Примеры:
Примеры:
1 сотка = 100 м2
2 сотки = 200 м2
10 соток = 1000 м2
Гектар (сокращенно: га) — это площадь, равная 10 000 м2. Например, если сказано что площадь какого-нибудь леса составляет 20 гектаров, то нужно понимать, что это двадцать квадратов площадью 10 000 м2 каждый, то есть:
20 га = 10 000 м2 × 20 = 200 000 м2
Прямоугольный параллелепипед и куб
Прямоугольный параллелепипед — это геометрическая фигура, состоящая из грáней, рёбер и вершин. На рисунке показан прямоугольный параллелепипед:
Желтым цветом показаны грáни параллелепипеда, чёрным цветом — рёбра, красным — вершины.
Прямоугольный параллелепипед обладает длиной, шириной и высотой. На рисунке показано где длина, ширина и высота:
Параллелепипед, у которого длина, ширина и высота равны между собой, называется кубом.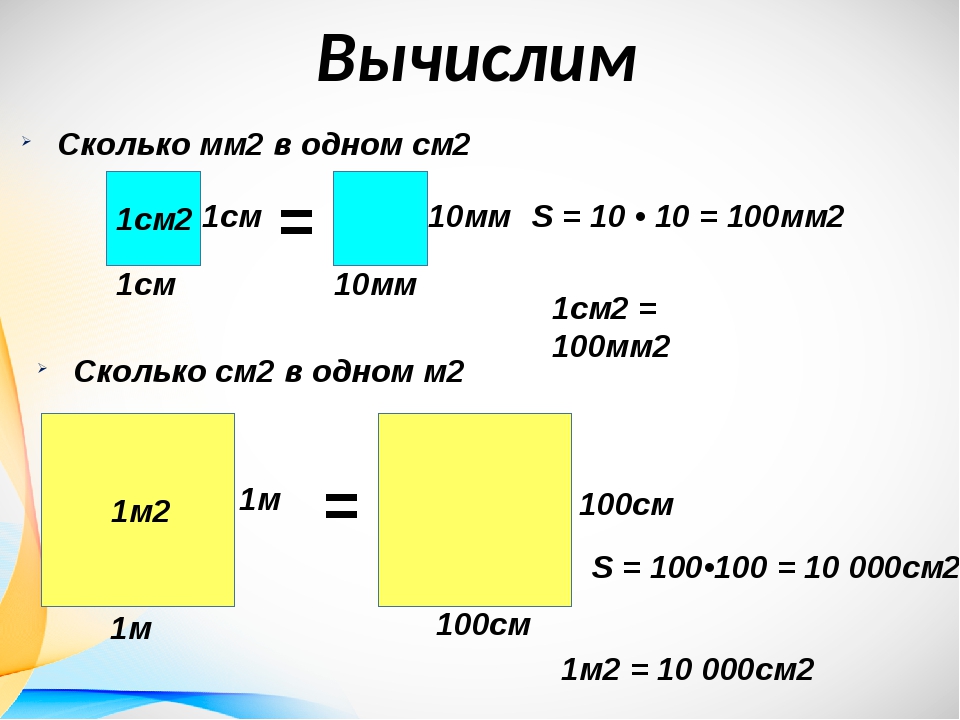 На рисунке показан куб:
На рисунке показан куб:
Объём геометрической фигуры
Объём геометрической фигуры — это число, которое характеризует вместимость данной фигуры.
Объём измеряется в кубических единицах. Под кубическими единицами подразумевают кубы длиной 1, шириной 1 и высотой 1. Например, 1 кубический сантиметр или 1 кубический метр.
Измерить объём какой-нибудь фигуры означает выяснить сколько кубических единиц вмещается в данную фигуру.
Например, объём следующего прямоугольного параллелепипеда равен двенадцати кубическим сантиметрам:
Это потому что в данный параллелепипед вмещается двенадцать кубов длиной 1 см, шириной 1 см и высотой 1 см:
Объём обозначается заглавной латинской буквой V. Одна из единиц измерения объема это кубический сантиметр (см3). Тогда объём V рассмотренного нами параллелепипеда равен 12 см3
V = 12 см3
Объём любого параллелепипеда вычисляют следующим образом: перемножают его длину, ширину и высоту .
Объём прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
V = abc
где, a — длина, b — ширина, c — высота
Так, в предыдущем примере мы визуально определили, что объём параллелепипеда равен 12 см3. Но можно измерить длину, ширину и высоту данного параллелепипеда и перемножить результаты измерений. Мы получим тот же результат
Объём куба вычисляется таким же образом, как и объём прямоугольного параллелепипеда — перемножают длину, ширину и высоту.
Например, вычислим объём куба, длина которого 3 см. У куба длина, ширина и высота равны между собой. Если длина равна 3 см, то равны этим же трём сантиметрам ширина и высота куба:
Перемножаем длину, ширину, высоту и получаем объём, равный двадцати семи кубическим сантиметрам:
V = 3 × 3 × 3 = 27 см³
Действительно, в исходный куб вмещается 27 кубиков длиной 1 см
При вычислении объёма данного куба мы перемножили длину, ширину и высоту. Получилось произведение 3 × 3 × 3. Это есть произведение трёх сомножителей, каждый из которых равен 3. Иными словами, произведение 3 × 3 × 3 является третьей степенью числа 3 и может быть записано в виде 33.
Получилось произведение 3 × 3 × 3. Это есть произведение трёх сомножителей, каждый из которых равен 3. Иными словами, произведение 3 × 3 × 3 является третьей степенью числа 3 и может быть записано в виде 33.
V = 33 = 27 см3
Поэтому третью степень числа называют кубом числа. При вычислении третьей степени числа a, человек тем самым находит объём куба, длиной a. Операцию возведения числа в третью степень по другому называют возведением в куб.
Таким образом, объём куба вычисляется по следующему правилу:
V = a3
Где a — длина куба.
Кубический дециметр. Кубический метр
Не все объекты нашего мира удобно измерять в кубических сантиметрах. Например, объём комнаты или дома удобнее измерять в кубических метрах (м3). А объём бака, аквариума или холодильника удобнее измерять в кубических дециметрах (дм3).
Другое название одного кубического дециметра – один литр.
1 дм3 = 1 литр
Перевод единиц измерения объёма
Единицы измерения объёма можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:
Пример 1. Выразить 1 кубический метр в кубических сантиметрах.
Один кубический метр это куб со стороной 1 м. Длина, ширина и высота этого куба равны одному метру.
Но 1 м = 100 см. Значит, длина, ширина и высота тоже равны 100 см
Вычислим новый объём куба, выраженный в кубических сантиметрах. Для этого перемножим его длину, ширину и высоту. Либо возведём число 100 в куб:
V = 1003 = 1 000 000 см3
Получается, что на один кубический метр приходится один миллион кубических сантиметров:
1 м3 = 1 000 000 см3
Это позволяет в будущем умножить любое количество кубических метров на 1 000 000 и получить объём, выраженный в кубических сантиметрах.
Чтобы перевести кубические метры в кубические сантиметры, нужно количество кубических метров умножить на 1 000 000.
А чтобы перевести кубические сантиметры в кубические метры, нужно наоборот количество кубических сантиметров разделить на 1 000 000.
Например, переведём 300 000 000 см3 в кубические метры. Рассуждать в этом случае можно так: «если 1 000 000 см3 это один кубический метр, то сколько раз 300 000 000 см3 будут содержать по 1 000 000 см3»
300 000 000 см3 : 1 000 000 см3 = 300 м3
Пример 2. Выразить 3 м3 в кубических сантиметрах.
Умножим 3 м3 на 1 000 000
3 м3 × 1 000 000 = 3 000 000 см3
Пример 3. Выразить 60 000 000 см3 в кубических метрах.
Узнаем сколько раз 60 000 000 см3 содержит по 1 000 000 см3. Для этого разделим 60 000 000 см3 на 1 000 000 см3
Для этого разделим 60 000 000 см3 на 1 000 000 см3
60 000 000 см3 : 1 000 000 см3 = 60 м3
Вместимость бака, банки или канистры измеряют в литрах. Литр это тоже единица измерения объема. Один литр равен одному кубическому дециметру.
1 литр = 1 дм3
Например, если вместимость банки составляет 1 литр, это значит что объём этой банки составляет 1 дм3. При решении некоторых задач может быть полезным умение переводить литры в кубические дециметры и наоборот. Рассмотрим несколько примеров.
Пример 1. Перевести 5 литров в кубические дециметры.
Чтобы перевести 5 литров в кубические дециметры, достаточно умножить 5 на 1
5 л × 1 = 5 дм3
Пример 2. Перевести 6000 литров в кубические метры.
Шесть тысяч литров это шесть тысяч кубических дециметров:
6000 л × 1 = 6000 дм3
Теперь переведём эти 6000 дм3 в кубические метры.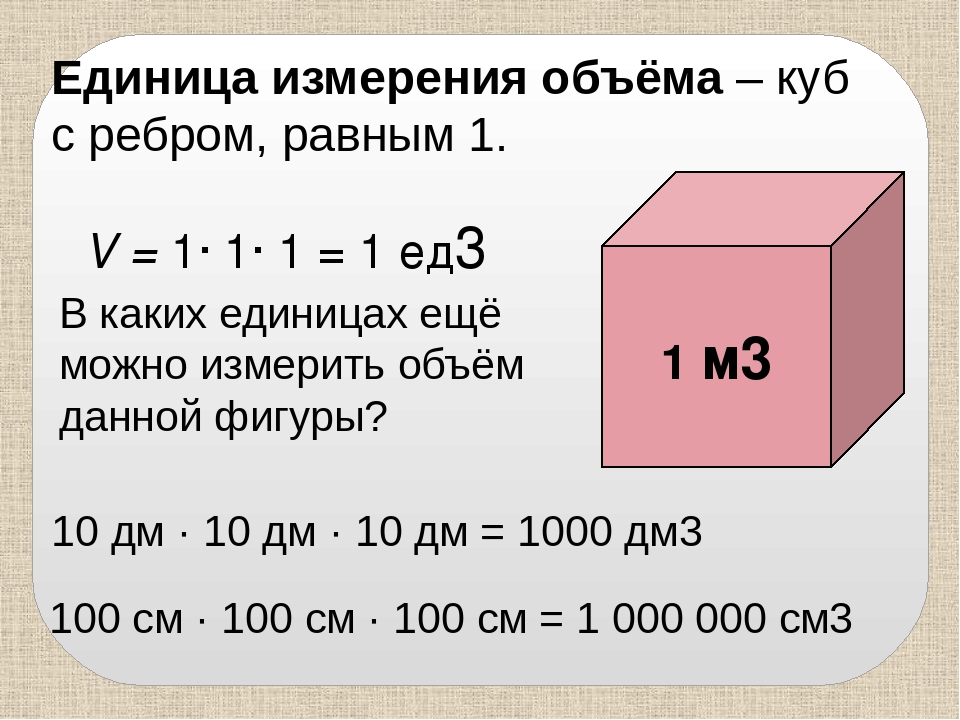
Длина, ширина и высота одного кубического метра равны 10 дм
Если вычислить объём этого куба в дециметрах, то получим 1000 дм3
V = 103= 1000 дм3
Получается, что одна тысяча кубических дециметров соответствует одному кубическому метру. А чтобы определить сколько кубических метров соответствуют шести тысячамл кубических дециметров, нужно узнать сколько раз 6 000 дм3 содержит по 1 000 дм3
6 000 дм3 : 1 000 дм3 = 6 м3
Значит, 6000 л = 6 м3.
Таблица квадратов
В жизни часто приходиться находить площади различных квадратов. Для этого каждый раз требуется возводить исходное число во вторую степень.
Квадраты первых 99 натуральных чисел уже вычислены и занесены в специальную таблицу, называемую таблицей квадратов.
Первая строка данной таблицы (цифры от 0 до 9) это единицы исходного числа, а первый столбец (цифры от 1 до 9) это десятки исходного числа.
Например, найдём квадрат числа 24 по данной таблице. Число 24 состоит из цифр 2 и 4. Точнее, число 24 состоит из двух десятков и четырёх единиц.
Итак, выбираем цифру 2 в первом столбце таблицы (столбце десятков), а цифру 4 выбираем в первой строке (строке единиц). Затем, двигаясь вправо от цифры 2 и вниз от цифры 4, найдём точку пересечения. В результате окажемся на позиции, где располагается число 576. Значит, квадрат числа 24 есть число 576
242 = 576
Таблица кубов
Как и в ситуации с квадратами, кубы первых 99 натуральных чисел уже вычислены и занесены в таблицу, называемую таблицей кубов.
Куб числа по таблице определяется таким же образом, как и квадрат числа. Например, найдём куб числа 35. Это число состоит из цифр 3 и 5. Выбираем цифру 3 в первом столбце таблицы (столбце десятков), а цифру 5 выбираем в первой строке (строке единиц). Двигаясь вправо от цифры 3 и вниз от цифры 5, найдём точку пересечения. В результате окажемся на позиции, где располагается число 42875. Значит, куб числа 35 есть число 42875.
В результате окажемся на позиции, где располагается число 42875. Значит, куб числа 35 есть число 42875.
353 = 42875
Задания для самостоятельного решения
Задача 1. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите периметр.
Решение
P = 2(a + b)
a = 6, b = 2
P = 2(6 + 2) = 12 + 4 = 16 см
Ответ: периметр прямоугольника равен 16 см.
Задача 2. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите площадь.
Решение
S = ab
a = 6, b = 2
S = 6 × 2 = 12 см2
Ответ: площадь равна 12 см2.
Задача 3. Площадь прямоугольника составляет 12 см2. Длина составляет 6 см. Найдите ширину прямоугольника.
Решение
S = ab
S = 12, a = 6, b = x
12 = 6 × x
x = 2
Ответ: ширина прямоугольника составляет 2 см.
Задача 4. Вычислите площадь квадрата со стороной 8 см
Решение
S = a2
a = 8
S = 82 = 64 см2
Ответ: площадь квадрата со стороной 8 см равна 64 см2
Задача 5. Вычислите объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см.
Решение
V = abc
a = 6, b = 4, c = 3
V = 6 × 4 × 3 = 72 см3.
Ответ: объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см равен 72 см3
Задача 6. Объем прямоугольного параллелепипеда составляет 200 см3. Найдите высоту параллелепипеда, если его длина равна 10 см, а ширина 5 см
Решение
V = abc
V = 200, a = 10, b = 5, c = x
200 = 10 × 5 × x
200 = 50x
x = 4
Ответ: высота прямоугольного параллелепипеда равна 4 см.
Задача 7. Площади земельного участка, засеянные пшеницей и льном, пропорциональны числам 4 и 5. На какой площади засеяна пшеница, если под льном засеяно 15 га
Решение
Число 4 отражает площадь, засеянную пшеницей. А число 5 отражает площадь, засеянную льном.
Сказано что площади, засеянные пшеницей и льном пропорциональны этим числам.
Проще говоря, во сколько раз изменяются числа 4 или 5, во сколько же раз изменится и площадь, которая засеяна пшеницей или льном. Льном засеяно 15 га. То есть число 5, которое отражает площадь, засеянную льном, изменилось в 3 раза.
Тогда число 4, которое отражает площадь засеянную пшеницей, нужно увеличить в три раза
4 × 3 = 12 га
Ответ: пшеницей засеяно 12 га.
Задача 8. Длина зернохранилища 42 м, ширина составляет длины, а высота – 0,1 длины. Определите сколько тонн зерна вмещает зернохранилище, если 1 м3 его весит 740 кг.Решение
a — длина
b — ширина
c — высота
a = 42 м
b = м
c = 42 × 0,1 = 4,2 м
Определим объем зернохранилища:
V = abc = 42 × 30 × 4,2 = 5292 м3
Определите сколько тонн зерна вмещает зернохранилище:
5292 × 740 = 3916080 кг
Переведём килограммы в тонны:
Ответ: зернохранилище вмещает 3916,08 тонн зерна.
Задача 9. 12. Бассейн имеет форму прямоугольного параллелепипеда, длина которого равна 5,8 м, а ширина – 3,5 м. Две трубы наполняют его водой в течение 13 ч 32 мин., причём через одну из них вливается 25 л/мин, а через вторую – 0,75 этого количества. Определите высоту (глубину) бассейна.
Решение
Определим сколько литров в минуту вливается через вторую трубу:
25 л/мин × 0,75 = 18,75 л/мин
Определим сколько литров в минуту вливается в бассейн через обе трубы:
25 л/мин + 18,75 л/мин = 43,75 л/мин
Определим сколько литров воды будет залито в бассейн за 13 ч 32 мин
43,75 × 13 ч 32 мин = 43,75 × 812 мин = 35 525 л
1 л = 1 дм3
35 525 л = 35 525 дм3
Переведём кубические дециметры в кубические метры. Это позволит вычислит объем бассейна:
35 525 дм3 : 1000 дм3 = 35,525 м3
Зная объём бассейна можно вычислить высоту бассейна. Подставим в буквенное уравнение V=abc имеющиеся у нас значения. Тогда получим:
Подставим в буквенное уравнение V=abc имеющиеся у нас значения. Тогда получим:
V = 35,525
a = 5.8
b = 3.5
c = x
35,525 = 5,8 × 3,5 × x
35,525 = 20,3 × x
x = 1,75 м
с = 1,75
Ответ: высота (глубина) бассейна составляет 1,75 м.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Как перевести см в квадратные метры
Онлайн калькулятор для перевода квадратных сантиметров в другие единицы измерения площади, такие как миллиметр квадратный, метр квадратный, километр квадратный, и д.р. Данный конвертер имеет высокий класс точности, историю вычислений и напишет сумму прописью.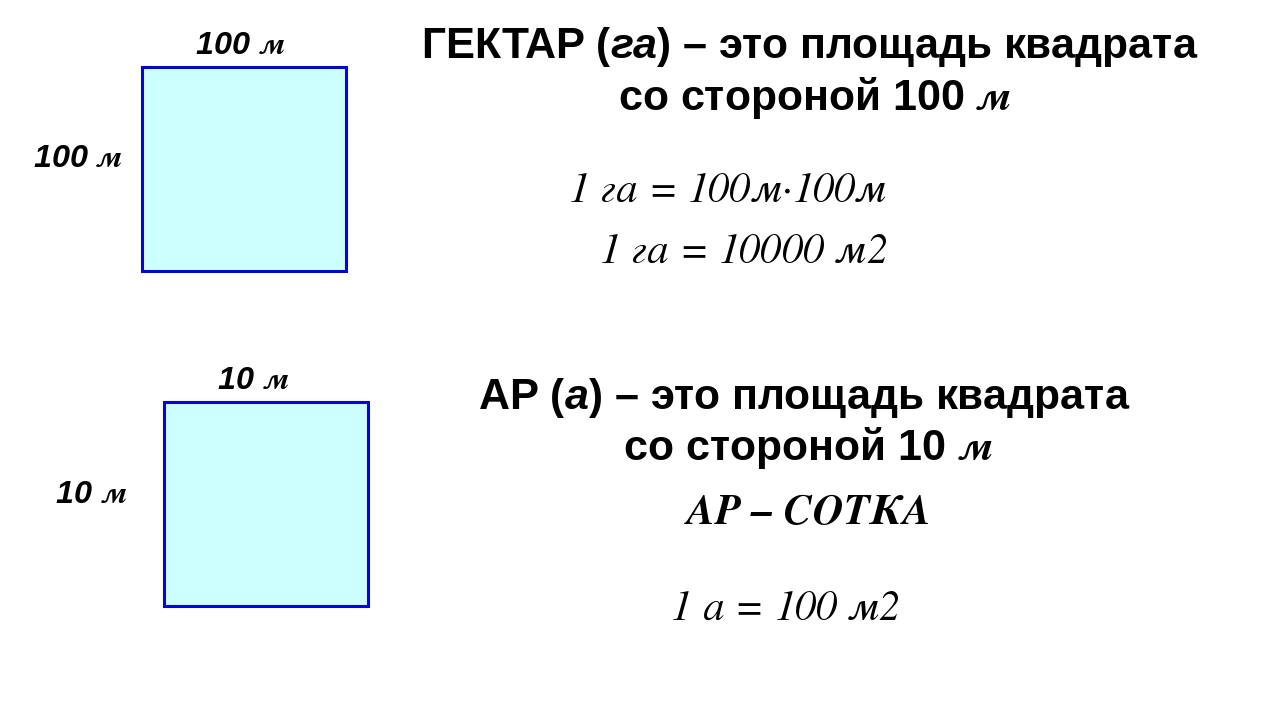
Сколько м 2 в см 2 – в 1 сантиметре квадратном 0.0001 метра квадратного.
100 квадратных сантиметров равно 1 метр квадратный
Квадратный сантиметр (обозначение см 2 ) – единица измерения площади, равная площади квадрата со стороной 1 сантиметр.
2 квадратных сантиметра = 200 миллиметров = 0.0002 квадратных метра;
3 квадратных сантиметра = 300 миллиметров = 0.0003 квадратных метра;
4 квадратных сантиметра = 400 миллиметров = 0.0004 квадратных метра;
5 квадратных сантиметра = 500 миллиметров = 0.0005 квадратных метра;
6 квадратных сантиметра = 600 миллиметров = 0.0006 квадратных метра;
8 квадратных сантиметра = 800 миллиметров = 0.0008 квадратных метра;
Как перевести квадратные метры в квадратные сантиметры?
Один квадратный метр равен 10000 квадратным сантиметрам:
Для сокращения записи принято использовать следующие обозначения:
1 квадратный метр = 1 м²;
1 квадратный сантиметр = 1 см²:
Другой вариант сокращённой записи —
1 квадратный метр = 1 кв.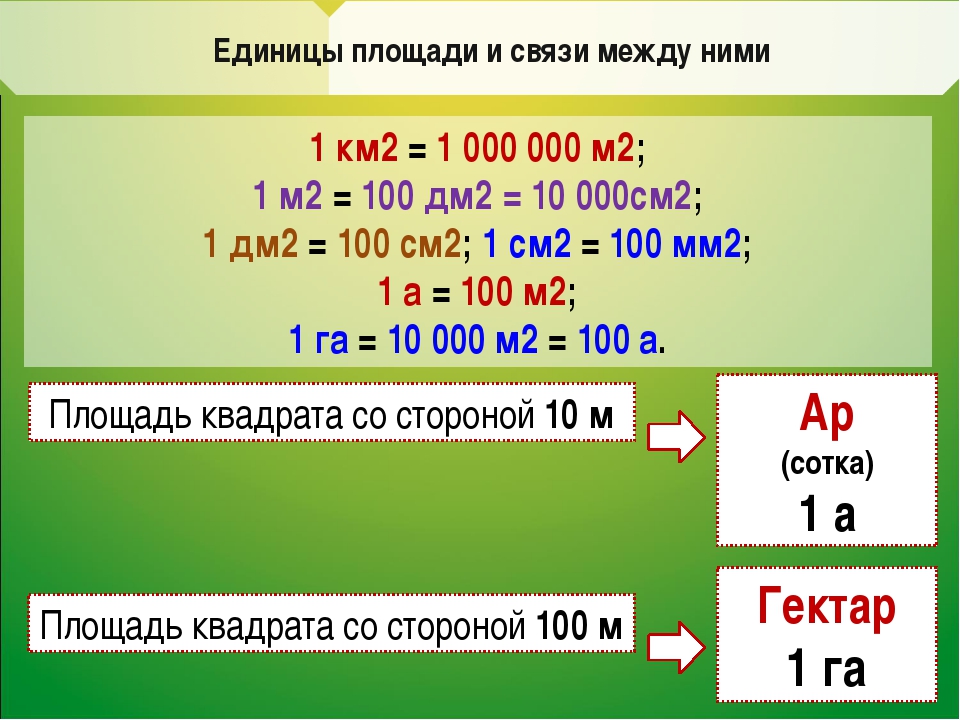 м
м
1 квадратный сантиметр = 1 кв.см
Это равенство не обязательно учить. Достаточно понять, как оно получено.
1 квадратный метр — это площадь квадрата со стороной 1 метр. В одном метре 100 сантиметров. Разделив каждую сторону квадрата на 100 частей по 1 сантиметру каждая, мы получим 100∙100=10000 квадратов со стороной 1 сантиметр.
Площадь каждого такого квадрата со стороной 1 см равна 1 квадратному сантиметру. Значит, площадь квадрата со стороной 1 м также равна 10000 см². Поэтому 1 м² = 10000 см².
Как перевести м² в см²?
Чтобы перевести квадратные метры в квадратные сантиметры, надо количество квадратных сантиметров умножить на 10000.
Формула перевода квадратных метров в квадратные сантиметры:
Перевод квадратных метров в квадратные сантиметры рассмотрим на конкретных примерах.
Выразить в квадратных сантиметрах:
При переводе квадратных метров в квадратные сантиметры количество квадратных метров умножаем на 10000:
1) 5 м²=5∙10000 см²=50000 см²;
2) 10 м²=10∙10000=100000 см²;
3) 7 м² 12 см²=7∙10000 см²+ 12 см²=70012 см²;
4) 28 м² 83 см²=28∙10000 см²+83 см²=28083 см²;
Онлайн конвертер метры в сантиметры (м² в см²)
Вы пересчитываете площадь из см² в метры²
Конвертируем см² в метр²
Сантиметры квадратные
Квадратный сантиметр (обозначение: «см²») – производная измерения площади.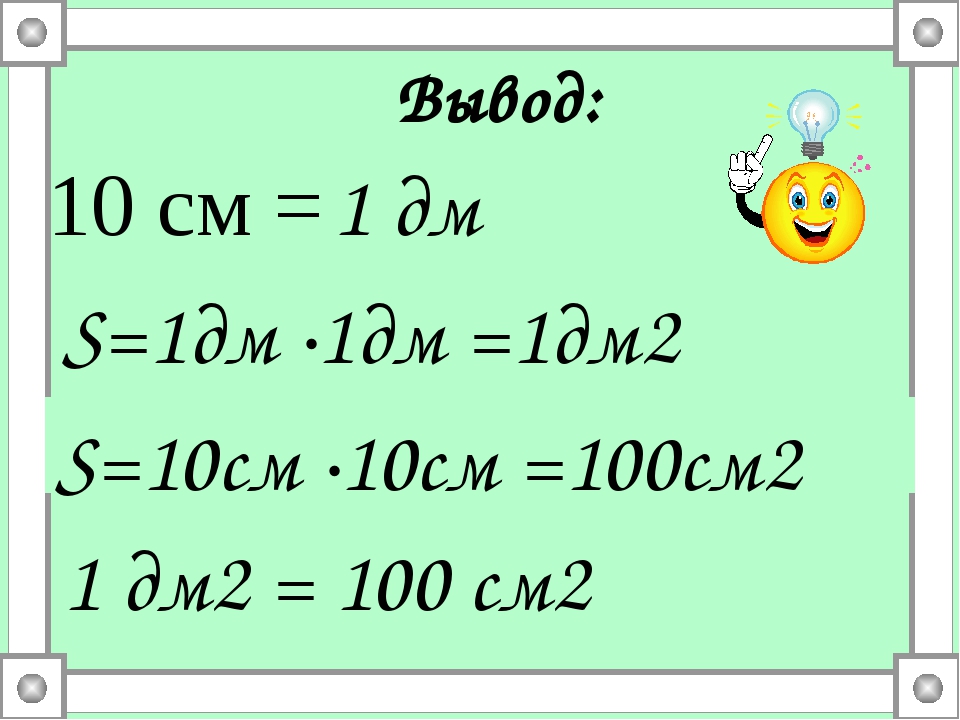 Эта единица образовывается от сантиметра. 1 квадратный сантиметр равен 0.0001 м².
Эта единица образовывается от сантиметра. 1 квадратный сантиметр равен 0.0001 м².
Метры
Квадратный метр (обозначение «м²») – это производная международная единица измерения площади. Она является исходной от известной меры Международной Системы Единиц «метр». Добавление и усечение приставки СИ создает кратные единицы, такие, как квадратный дециметр, квадратный гектометр.
методы расчета и формулы, примеры и объём помещения по формуле, сложные фигуры
При ремонте, покупке материалов нужно знать площадь помещений. Говорят еще «квадратура». Как посчитать площадь комнаты в квадратных метрах, что для этого нужно — будем рассматривать в статье.
Немного теории
Как найти площадь различных фигур, проходили еще в начальной школе. Было это давно, так что «обновить» информацию может быть полезно. Будем рассматривать только то, что может иметь отношение к полу. Итак, начнем с самого простого — единиц измерения.
Чтобы посчитать площадь комнаты в квадратных метрах, нужен будет карандаш, рулетка и некоторый багаж знаний
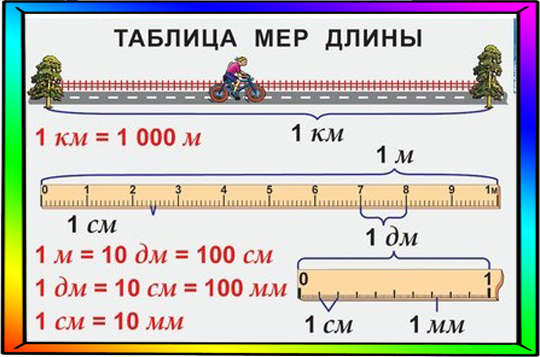
Что такое 1 см² и 1 м²
Площадь любой фигуры измеряется в квадратных метрах или в квадратных сантиметрах. Обозначение см² или м², может встречаться написание кв.м, кв. см., кв. метры, кв. сантиметры и другие вариации.
Обозначение см² или м², может встречаться написание кв.м, кв. см., кв. метры, кв. сантиметры и другие вариации.
Один квадратный сантиметр — это площадь квадрата со стороной 1 см. Если нарисовать такой квадрат, стороны которого равны 1 см, то заштрихованная часть (на рисунке красным или синим) и будет один квадратный сантиметр.
Соответственно, квадрат со стороной один метр — 1 м — имеет площадь один квадратный метр. Тот самый «квадрат площади». То есть, это квадратный участок пола (или стены) со стороной в один метр — 1 м².
В одном квадратном метре десять тысяч квадратных сантиметров: 1 м² = 10000 см².
Формулы
Это то, что касалось единиц измерения и их соответствия. Но наши помещения, слава богу, больше чем один квадратный метр. Как посчитать площадь комнаты? Сколько в ней квадратных метров? Обычно комната имеет форму прямоугольника, реже — квадрата. Значит, надо будет вспомнить формулы нахождения площади квадрата и прямоугольника.
При помощи очень простых формул, можно рассчитать площадь прямоугольника и квадрата
Надо длины сторон прямоугольника перемножить. Получим искомую площадь. Давайте потренируемся.
Получим искомую площадь. Давайте потренируемся.
- Имеем прямоугольник со сторонами 80 см и 50 см. Перемножаем эти цифры: 80 * 50 = 4000 см². Это и будет его площадь.
- Стороны 322 см и 300 см. Получим: 322*300 = 96000 см².
- Есть квадрат со стороной 60 см. Его площадь — 60 * 60 = 3600 см².
В случае с квадратом длину стороны можно возвести в квадрат — получится одно и то же. Но можно не морочить голову. Проще помнить, что надо стороны умножить.
Простейший калкулятор для расчета площади прямоугольной комнаты.
Перевод квадратных сантиметров в квадратные метры
Когда имеем дело с сотнями сантиметров, удобнее и проще считать в метрах. Мы знаем, что в одном метре сто сантиметров. Давайте решим те же примеры, но переведем сантиметры в метры:
- 80 см = 0,8 м; 50 см = 0,5 м. Перемножаем 0,8*0,5 = 0,4 м². То есть, 0,4 квадратных метра.
- 322 см это 3,22 м; 300 см это 3 м. Теперь умножаем полученные цифры: 3,22 * 3 = 9,6 м².

- 60 см равны 0,6 м. Площадь квадрата с такой стороной 0,6*0,6 = 0,36 м².
Цифры получаются намного меньше, запомнить их проще. И если мы хотим посчитать площадь комнаты в квадратных метрах, ее размеры мы меряем в метрах, а не сантиметрах. Можно перевести квадратные сантиметры в квадратные метры. Как уже говорили, в одном квадратном метре содержится десять тысяч квадратных сантиметров.
Соотношение квадратных сантиметров и квадратных метров
Если же у вас есть площадь в квадратных сантиметрах, чтобы перевести ее в квадратные метры, цифру надо разделить на 10 000. Например:
- 4000 см² / 10000 = 0,4 м²;
- 96000 см² / 10000 = 9,6 м²;
- 3600 см²/ 10000 = 0,36 м².
Как видите, все просто. Надо только запомнить основные положения и посчитать площадь комнаты в квадратных метрах будет совсем несложно. Нужно будет предварительно провести измерения, а потом заняться расчетами.
Рассчитать площадь комнаты, часто надо при закупке материалов для строительства или ремонта. Например, некоторые виды напольного покрытия продают на квадраты (то есть, на квадратные метры). Чтобы правильно рассчитать его количество, надо знать площадь пола (часто говорят квадратура комнаты, что по сути одно и то же).
Например, некоторые виды напольного покрытия продают на квадраты (то есть, на квадратные метры). Чтобы правильно рассчитать его количество, надо знать площадь пола (часто говорят квадратура комнаты, что по сути одно и то же).
Можно найти площадь комнаты зная длину и ширину
Измерения
Берем рулетку, листок бумаги, карандаш и калькулятор. На бумаге рисуем план комнаты. При помощи рулетки измеряем длины всех стен. Измерения проводим на уровне пола — если постройка старая, велика вероятность того, что стены «завалены» в ту или другую сторону. Тем более что определяем площадь пола, так что логичнее измерять вплотную к стенам, но мерную ленту тянуть по полу.
На схеме проставляем измерения. Лучше всего в метрах. Точность измерений — до сантиметра. Это понадобится при покупке материалов, которые продаются на погонные метры — линолеум, ковролин или другие рулонные покрытия. Чтобы посчитать площадь комнаты в квадратных метрах, тоже желательна такая точность. Хоть можно, конечно, и округлить. Но лучше это сделать уже получив результат.
Но лучше это сделать уже получив результат.
Как высчитать квадратуру комнаты
Имея длину и ширину комнаты прямоугольной формы, цифры надо просто перемножить. На рисунке выше такая комната нарисована справа. Длинная стена равна 7 м, короткая — 4 метрам. Перемножаем 7*4 = 28 квадратных метров. Это и есть площадь этого помещения, пола.
Другими словами, мы нашли квадратуру. Используя эту цифру, можно покупать напольное покрытие. Но надо иметь в виду, что требуется некоторый запас — на подгонку, подрезку.
Чем сложнее схема укладки и чем больше фрагменты напольного покрытия, тем запас должен быть больше.
Часто комната не прямоугольная, а имеет более сложную форму. Чтобы посчитать площадь такой комнаты в квадратных метрах, ее разбивают на простые фигуры. Если удается — на прямоугольники или квадраты. Например, Г-образную комнату разбивают на два прямоугольника. Затем считают площадь каждого прямоугольника отдельно, потом их складывают.
Как найти площадь комнаты сложной формы
- Считаем большой прямоугольник: 5 м * 4,35 м = 21,75 м².

- Находим квадратуру маленького: 2,5 м * 2,65 м = 6,625 м².
- Площадь пола в этом помещении равна сумме 21,75 м² + 6,625 м² = 28,375 м².
При покупке материалов, проще пользоваться округленными значениями. Чаще всего говорят, что в этом помещении 28,4 квадрата.
Если помещение имеет участок «срезанной» стены, как на рисунке ниже, проще всего дорисовать прямоугольник так, чтобы косая делила его на два треугольника. В этом случае снова-таки получаем Г-образную комнату. Как высчитать ее площадь уже знаем.
Получается, ищем площадь трех прямоугольников
А недостающий участок — это половина маленького прямоугольника. То есть, находим площадь этого маленького прямоугольника, делим ее пополам и прибавляем к размерам Г-образного участка.
Приведем пример расчета подставляя произвольные значения:
- Большой прямоугольник: 1,75 м *1,93 м = 3,3775 м². Для простоты округлим до 3,38 м².
- Средний прямоугольник: 1,18 м * 0,57 м = 0,6726 м².
 Снова округлим до 0,67 м².
Снова округлим до 0,67 м². - Самый маленький прямоугольник (в нашем случае это будет квадрат): 0,57 м *0,57 м = 0,3249 м2, после округления имеем 0,33 м².
- Чтобы найти общую площадь складываем квадратуру двух прямоугольников и добавляем половину площади последнего, самого маленького участка. 3,38 + 0,67 +0,33/2 = 3,38 + 0,67 +0,17 = 4,22 м².
Такая методика — разбиение на простые фигуры — самый удобный и простой метод. Всегда стоит стараться преобразовать сложную фигуру в набор простых. Правда, измерений может потребоваться больше.
Площадь квартиры
Так как ремонт — это «бедствие», которое периодически нас посещает, лучше сделать план всей квартиры с подробными замерами. На этом же плане проставьте площади каждого помещения. После того, как рассчитаете квадратуру всех комнат, сложите цифры и получите метраж квартиры.
Один вариант может быть как на рисунке выше — для того, чтобы знать именно площади каждого помещения. Это потребуется для закупки материалов. Но нужен будет еще план, на котором будут все длины. Простенки, ширина окон, дверей и т.д. Это потребуется, например, для разработки схем укладки ламината, напольной плитки или других покрытий. Нужен будет такой план и при планировании теплого пола.
Но нужен будет еще план, на котором будут все длины. Простенки, ширина окон, дверей и т.д. Это потребуется, например, для разработки схем укладки ламината, напольной плитки или других покрытий. Нужен будет такой план и при планировании теплого пола.
Источник: https://chudopol.ru/raschet-ploshhadi
Как посчитать квадратуру комнаты, стен, потолка, пола
Периодически нам требуется знать площадь и объем комнаты. Эти данные могут понадобиться при проектировании отопления и вентиляции, при закупке стройматериалов и еще во многих других ситуациях.
Также периодически требуется знать площадь стен. Все эти данные вычисляются легко, но предварительно придется поработать рулеткой — измерять все требуемые габариты.
Площадь комнаты в квадратных метрах
Посчитать несложно, требуется только вспомнить простейшие формулы а также провести измерения. Для этого нужны будут:
- Рулетка. Лучше — с фиксатором, но подойдет и обычная.
- Бумага и карандаш или ручка.

- Калькулятор (или считайте в столбик или в уме).
Набор инструментов нехитрый, найдется в каждом хозяйстве. Проще измерения проводить с помощником, но можно справиться и самостоятельно.
Для начала надо измерить длину стен. Делать это желательно вдоль стен, но если все они заставлены тяжелой мебелью, можно проводить измерения и посередине. Только в этом случае следите чтобы лента рулетки лежала вдоль стен, а не наискосок — погрешность измерений будет меньше.
Прямоугольная комната
Если помещение правильной формы, без выступающих частей, вычислить площадь комнаты просто. Измеряете длину и ширину, записываете на бумажке. Цифры пишите в метрах, после запятой ставите сантиметры. Например, длина 4,35 м (430 см), ширина 3,25 м (325 см).
Найденные цифры перемножаем, получаем площадь комнаты в квадратных метрах. Если обратимся к нашему примеру, то получится следующее: 4,35 м * 3,25 м = 14,1375 кв. м. В данной величине оставляют обычно две цифры после запятой, значит округляем. Итого, рассчитанная квадратура комнаты 14,14 квадратных метров.
Итого, рассчитанная квадратура комнаты 14,14 квадратных метров.
Помещение неправильной формы
Если надо высчитать площадь комнаты неправильной формы, ее разбивают на простые фигуры — квадраты, прямоугольники, треугольники. Потом измеряют все нужные размеры, производят расчеты по известным формулам (есть в таблице чуть ниже).
Перед тем как посчитать площадь комнаты, тоже проводим изменения. Только в этом случае цифр будет не две, а четыре: добавится еще длина и ширина выступа. Габариты обоих кусков считаются отдельно.
Один из примеров — на фото. Так как и то, и другое — прямоугольник, площадь считается по той же формуле: длину умножаем на ширину. Найденную цифру надо отнять или прибавить к размеру помещения — в зависимости от конфигурации.
Покажем на этом примере как посчитать площадь комнаты с выступом (изображена на фото выше):
- Считаем квадратуру без выступа: 3,6 м * 8,5 м = 30,6 кв. м.
- Считаем габариты выступающей части: 3,25 м * 0,8 м = 2,6 кв.
 м.
м. - Складываем две величины: 30,6 кв. м. + 2,6 кв. м. = 33,2 кв. м.
Еще бывают помещения со скошенными стенами. В этом случае разбиваем ее так, чтобы получились прямоугольники и треугольник (как на рисунке ниже). Как видите, для данного случая требуется иметь пять размеров. Разбить можно было по-другому, поставив вертикальную, а не горизонтальную черту. Это не важно. Просто требуется набор простых фигур, а способ их выделения произвольный.
В этом случае порядок вычислений такой:
- Считаем большую прямоугольную часть: 6,4 м * 1,4 м = 8,96 кв. м. Если округлить, получим 9, 0 кв.м.
- Высчитываем малый прямоугольник: 2,7 м * 1,9 м = 5,13 кв. м. Округляем, получаем 5,1 кв. м.
- Считаем площадь треугольника. Так как он с прямым углом, то равен половине площади прямоугольника с такими же размерами. (1,3 м * 1,9 м) / 2 = 1,235 кв. м. После округления получаем 1,2 кв. м.
- Теперь все складываем чтобы найти общую площадь комнаты: 9,0 + 5,1 + 1,2 = 15,3 кв.
 м.
м.
Планировка помещений может быть очень разнообразной, но общий принцип вы поняли: делим на простые фигуры, измеряем все требуемые размеры, высчитываем квадратуру каждого фрагмента, потом все складываем.
Формулы расчета площади и периметра простых геометрических фигур
Еще одно важное замечание: площадь комнаты, пола и потолка — это все одинаковые величины. Отличия могут быть если есть какие-то полу-колоны, не доходящие до потолка. Тогда из общей квадратуры вычитается квадратура этих элементов. В результате получаем площадь пола.
Как рассчитать квадратуру стен
Определение площади стен часто требуется при закупке отделочных материалов — обоев, штукатурки и т.п. Для этого расчета нужны дополнительные измерения. К имеющимся уже ширине и длине комнаты нужны будут:
- высота потолков;
- высота и ширина дверных проемов;
- высота и ширина оконных проемов.
Все измерения — в метрах, так как квадратуру стен тоже принято измерять в квадратных метрах.
Так как стены прямоугольные, то и площадь считается как для прямоугольника: длину умножаем на ширину. Таким же образом вычисляем размеры окон и дверных проемов, их габариты вычитаем. Для примера рассчитаем площадь стен, изображенных на схеме выше.
- Стена с дверью:
- 2,5 м * 5,6 м = 14 кв. м. — общая площадь длинной стены
- сколько занимает дверной проем: 2,1 м *0,9 м = 1,89 кв.м.
- стена без учета дверного проема — 14 кв.м — 1,89 кв. м = 12,11 кв. м
- Стена с окном:
- квадратура маленьких стен: 2,5 м * 3,2 м = 8 кв.м.
- сколько занимает окно: 1,3 м * 1,42 м = 1,846 кв. м, округляем, получаем 1,75 кв.м.
- стена без оконного проема: 8 кв. м — 1,75 кв.м = 6,25 кв.м.
Найти общую площадь стен не составит труда. Складываем все четыре цифры: 14 кв.м + 12,11 кв.м. + 8 кв.м + 6,25 кв.м. = 40,36 кв. м.
Объем комнаты
Для некоторых расчетов требуется объем комнаты. В этом случае перемножаются три величины: ширина, длинна и высота помещения. Измеряется данная величина в кубических метрах (кубометрах), называется еще кубатурой. Для примера используем данные из предыдущего пункта:
Измеряется данная величина в кубических метрах (кубометрах), называется еще кубатурой. Для примера используем данные из предыдущего пункта:
- длинна — 5,6 м;
- ширина — 3,2 м;
- высота — 2,5 м.
Если все перемножить, получаем: 5,6 м * 3,2 м * 2,5 м = 44,8 м3. Итак, объем помещения 44,8 куба.
Источник: https://stroychik.ru/raznoe/raschet-ploshhadi-i-obema
Как посчитать квадратуру комнаты, стен, потолка, пола
Временами требуется узнать площадь или объем комнаты, чтобы произвести расчеты на приобретение различных материалов для строительства или ремонта помещения. В процессе ремонта приходится измерять площадь стен, чтобы определиться с количеством обоев или других отделочных материалов. Как правило, расчеты начинаются с замеров. Замеры осуществляются с помощью рулетки или другими способами.
Как посчитать площадь комнаты?
Это не сложный процесс, поскольку существуют определенные формулы. В данном случае, достаточно определиться с размерами.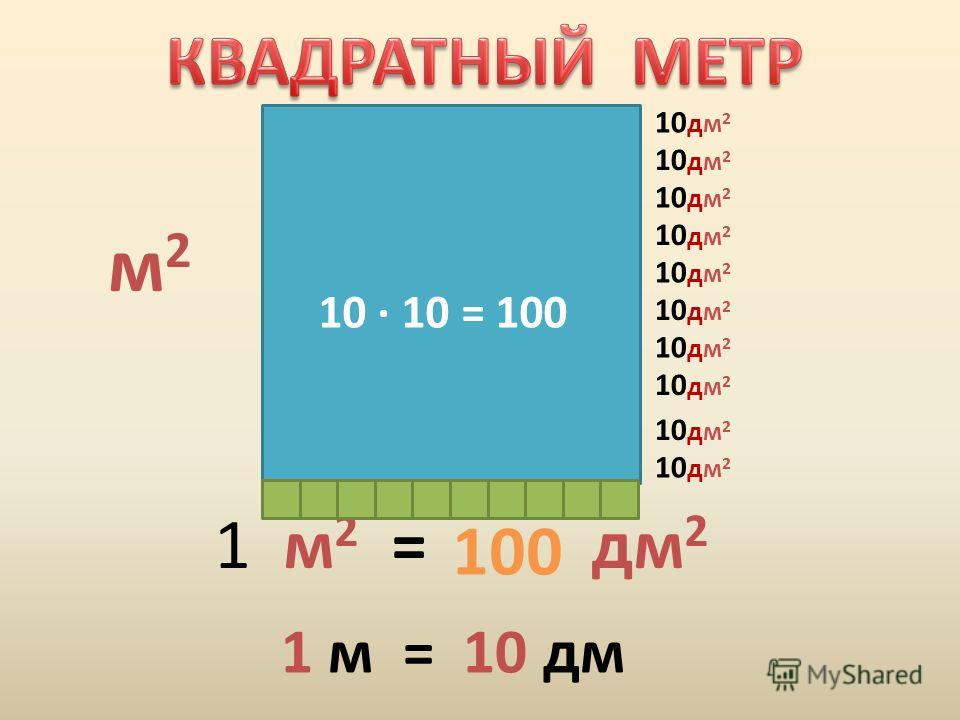 Для этого необходимо:
Для этого необходимо:
- приобрести рулетку, самую обычную, желательно на 5 метров;
- взять бумагу, карандаш или ручку;
- иметь калькулятор, хотя не сложно посчитать и на бумаге.
С помощью этого, минимального набора приспособлений и осуществляются все необходимые расчеты. Лучше конечно, иметь помощника, но, в крайнем случае, можно все делать самому. Габариты комнаты измеряются вдоль стен, если они не заставлены мебелью.
Если нужны точные размеры, то лучше мебель отставить и освободить стены. Лишь после этого рекомендуется производить все измерения. При этом, следует учитывать тот фактор, что правильных комнат, с прямыми углами практически не существует, если дело касается помещений, сооруженных еще в советские времена.
В связи с этим, необходимо весьма серьезно отнестись к процессу измерения.
Прямоугольные помещения
Если комната имеет правильную (относительно) прямоугольную форму, без всевозможных выступов или ниш, то площадь ее вычисляется довольно просто.
Для начала, нужно измерить длину и ширину комнаты, после чего результаты записать на бумажке, чтобы не забыть. Измерения можно производить как в метрах, так и в сантиметрах.
Если замеры осуществляются в метрах, то после целых значений метров ставится запятая, а потом пишутся сантиметры. Например, 4 метра, 35 сантиметров следует записать: 4,35 м.
Измерив длину, например, 2,35 м и ширину 1,4 м, данные перемножаются. Например: 2,35 м х 1,4 м. В результате получается 3,290 м2 или 3,29 м2. Как правило, после запятой всегда оставляется две цифры.
Если их больше, то значение округляется по правилам, которые излагались еще в начальных классах школы. При этом, можно округлять или до метров, или до сантиметров, в зависимости от требуемой точности.
В основном, достаточно измерять с точностью до метров и лишь изредка требуется точность до сантиметров.
Комната неправильной формы
Не все комнаты имеют правильную форму. Довольно часто встречаются помещения с наличиями выступов различной формы. В таких случаях, помещения делятся на отдельные квадраты, прямоугольники или треугольники, в зависимости от конфигурации выступов. Затем измеряются все выступы, после чего рассчитывают их площадь и все полученные результаты суммируют.
В таких случаях, помещения делятся на отдельные квадраты, прямоугольники или треугольники, в зависимости от конфигурации выступов. Затем измеряются все выступы, после чего рассчитывают их площадь и все полученные результаты суммируют.
На фото выше представлен пример, где в комнате имеется выступ прямоугольной формы. В таком случае, площадь комнаты вычисляется следующим образом:
- Подсчитывается общая площадь без выступа: 3,6м х 8,5м = 30,6м2.
- Вычисляется площадь выступа: 3,25м х 0,8м = 2,6м2.
- Полученные результаты складываются: 30,6м2 + 2,6м2 = 33,2м2.
Встречаются комнаты со скошенными стенами. Поступают следующим образом: стена разбивается так, что получается прямоугольник и треугольник (см. рисунок ниже). В результате для расчетов, необходимо иметь пять размеров. Впоследствии, вычисляют отдельно площади фигур, а потом все результаты либо складывают, либо вычитаются, в зависимости от характера выступа.
Квадратуру обсчитывают в таком порядке:
- Подсчитывается основная прямоугольная часть: 6,5 м х 1,4 м = 8,96м2.
 Округляя получаем 9,0 м2.
Округляя получаем 9,0 м2. - Вычисляется площадь малого прямоугольника: 2,7м х 1,9м = 5,13м2. При округлении получаем 5,0 м2.
- Подсчитывается площадь треугольника, имеющего прямой угол (1,3м х 1,9м) / 2 = 1,235м2. Округлив получится 1 м2.
- В заключение, полученные результаты складываются: 9+5+1 = 15 м2.
Подобная точность вычислений абсолютно приемлема. Как правило, планировка помещений бывает разнообразной, но правило подсчетов абсолютно одинаковы: все делится на отдельные, независимые фигуры, подсчитывается площадь отдельных фигур, а потом все складывается, а может и вычитается, в зависимости от конфигурации выступов. Особенно это актуально при определении площади пола или потолка.
Как подсчитать площадь стен
Квадратуру стен необходимо знать, когда планируется закупка отделочных материалов, таких как обои, шпаклевка, краска и другие. Если это глухая стена, то здесь все просто – измеряется высота и длина стены, после чего результаты перемножаются.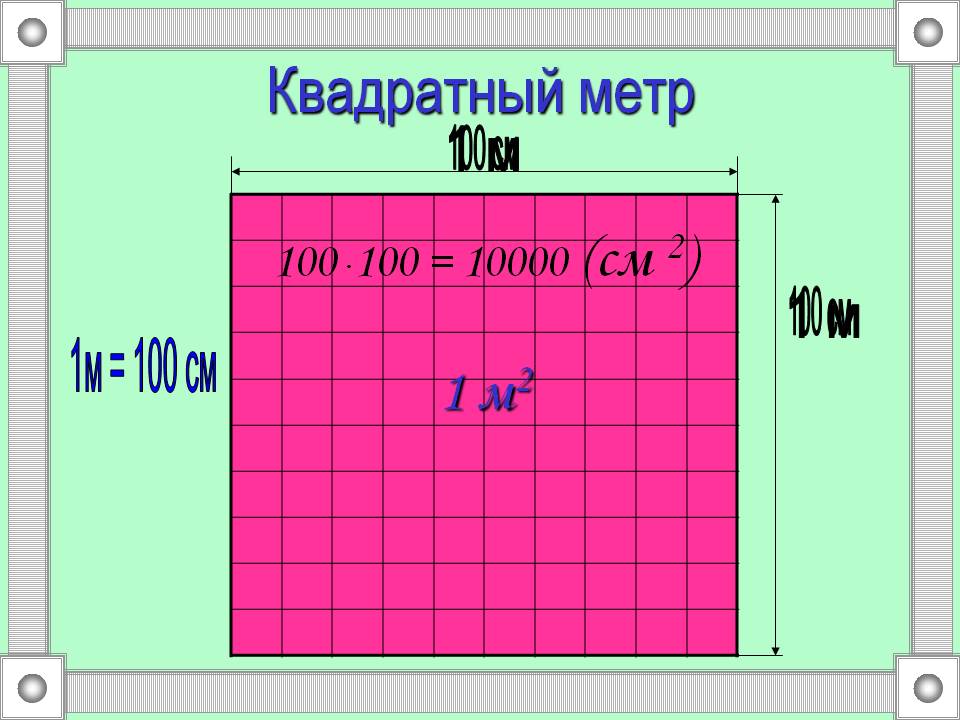 Если в стене расположен оконный или дверной проем, то нужно определить, какую площадь они занимают и отнять от общей площади стены. Поэтому:
Если в стене расположен оконный или дверной проем, то нужно определить, какую площадь они занимают и отнять от общей площади стены. Поэтому:
- измеряют высоту стен и их ширину;
- узнают высоту и ширину дверных проемов;
- измеряют высоту и ширину оконных проемов.
Глухая стена
- 2,5 м х 6,0м = 15 м2 – площадь глухой стены.
Стена с дверным проемом:
- Общая площадь стены: 2,5м х 6,0м = 15м2.
- Площадь дверного проема: 2,1м х 1,0м = 2,1м2.
- Площадь стены без дверей: 15м2 – 2,1м2 = 12,9м2.
Стена с оконным проемом:
- Общая площадь стены: 2,5м х 4м = 10м2.
- Площадь оконного проема: 1,3м х 1,5м = 1,95м2.
- Площадь стены без окна: 10 м2 – 1,95 м2 = 8,05м2.
Как правило, вычисляют общую площадь всех стен. Для этого берут и складывают полученные результаты площадей каждой стены. Например: 15м2 + 12,9м2 + 10м2 + 8,05м2 = 45,95м2.
Как определить объем комнаты
Иногда, для некоторых расчетов необходимо знать, какой объем занимает комната. Для подобных расчетов нужно знать еще одну цифру: не только длину и ширину, но и высоту комнаты. В результате расчетов получается кубатура (объем) комнаты, которая обозначается в метрах кубических. Например:
- длина помещения – 6 м;
- ширина помещения – 4 м;
- высота помещения – 2,5 м.
Теперь нужно все показатели перемножить: 6м х 4м х 2,5м = 60м3. Итак, получается, что объем помещения составляет 60 м3.
Подобная точность расчетов на конечный результат особо не влияет, поскольку мало кто приобретает облицовочные материалы исходя из подобных расчетов. Как правило, приобретают любые облицовочные материалы с некоторым запасом.
Если, например, считают количество керамической плитки, то расчеты производят по количеству штук, исходя из схемы укладки. Даже в этом случае, ее берут с некоторым избытком. Это связано еще и с тем, что возможны нештатные ситуации, связанные с порчей облицовочного материала.
Особенно это актуально, когда работы выполняются самостоятельно, без привлечения профессионалов.
Это относится и к таким материалам, как обои, линолеум, ламинат, различная вагонка, сайдинг и т.д. Нужно всегда помнить, что при работах появляются отходы и, причем, их может быть немало, если размеры произвольные, без учета применения тех или иных материалов.
Подобный подход особенно актуален при укладке линолеума, который имеет стандартные размеры по ширине. Что касается его длины, то тут нужно очень точно все измерить и всегда сантиметров 10, но добавить. Если просчитаться, то это может дорого обойтись.
Источник: https://stroyday.com/kak-poschitat-kvadraturu-komnaty-sten-potolka-pola/
Как правильно и быстро посчитать квадратные метры стен, пола и потолка? Объём помещения по формуле, сложные фигуры
Проверить работу строителей, определить объёмы работ и материалов легко, зная как посчитать квадратные метры пола или стен помещения с помощью простых геометрических формул, несложных вычислений и нехитрых приёмов.
В строительстве и отделочных работах почти все расценки на работы сведены к стоимости за квадратный метр. Квадратура поверхностей нужна и для подсчёта расхода материала (смотрите еще: советы для дома).
Метр квадратный это сколько?
Квадратным метром называется единица измерения площади, принятая в международной системе единиц, СИ. 1м² равен площади квадрата со стороной 1 м.
Знание простых правил и нескольких геометрических формул для подсчёта количества квадратных метров стен, полов, потолка позволит избежать ошибок в вычислениях и правильно определить нужные величины.
Инструменты для подсчёта
Для замера и расчёта понадобятся следующие предметы и инструменты:
- измерительная рулетка, необходимая длина рулетки 3-5 м;
- карандаш;
- лист бумаги для записей;
- калькулятор;
- строительный угольник.
Угольником размечают перпендикуляры – линии, пересекающиеся под прямым углом.
Площадь комнаты
Знание метража комнаты пригодится для определения стоимости полового покрытия, отделки потолка, количества и мощности осветительных приборов. Замеряя квадратуру помещения, проверяют соответствие площади, заявленной по проекту.
Измерения стен удобнее производить снизу, на уровне плинтуса. Сомнения в правильной форме помещения устраняют при помощи измерения диагоналей. Если диагонали комнаты равны, то углы – прямые, а помещение – прямоугольное.
Квадрат или прямоугольник
Самая распространенная форма комнаты в плане – квадратная или прямоугольная. Подсчёт квадратуры по полу при этом не составит особого труда:
- измеряют с помощью рулетки длину и ширину комнаты;
- перемножают цифры между собой, записывая результат на бумагу;
- выступы, колонны обмеряют, площадь элементов считают по тем же принципам, перемножая два размера;
- получившиеся цифры вычитают из площади комнаты.

При этом площадь потолка считают по тому же принципу, то есть умножают длину на ширину за вычетом технологических проемов, если таковые имеются.
Помещение неправильной формы
Эркеры, мансарды и комнаты домов со сложной архитектурой в плане часто имеют неправильную форму. Метраж нестандартной комнаты с полукругами, выступами, множеством углов подсчитать сложнее. Облегчают задачу, используя принцип деления сложных фигур на простые.
Пол, представляя как составную фигуру мысленно или отображая на бумаге, разделяют на стандартные геометрические элементы. Затем вычисляют площадь элементов по одному и складывают полученные величины.
Г-образные, Т-образные формы помещения в плане разбивают на прямоугольники и квадраты. Полукруглые поверхности принимают как часть круга.
Количество квадратных метров пола комнаты, в основе которой лежит трапеция, можно высчитать двумя способами:
- представив трапецию, как сочетание квадрата с двумя треугольниками.
 Получив значение фигур, цифры складывают;
Получив значение фигур, цифры складывают; - по формуле площади трапеции.
Для подсчёта по формуле измеряют две противоположные длинные стены, эти размеры дадут значения оснований. Значение высоты определяют путём замера перпендикуляра, проведённого от одного из углов меньшего основания к большему.
Формула площади трапеции S=1/2(А+В)*Н, где:
- S – искомая величина, площадь трапеции;
- А – основание трапеции;
- В – основание трапеции;
- Н – высота трапеции.
Площадь трапециевидной комнаты – половина суммы числовых значений оснований, умноженных на высоту.
Объем комнаты
Объём измеряется в кубических метрах. Единица записывается как 1 м³.
- С точки зрения геометрии, помещение как фигура представляет собой шестигранник.
- Измерив длину, ширину и высоту комнаты прямоугольной формы, перемножив полученные измерения, получают объём простого помещения.

- Объём помещения сложной формы вычисляют следующим путём:
- пол комнаты разбивают на простые геометрические фигуры;
- вычисляют квадратуру каждой фигуры;
- полученные значения складывают и умножают на высоту до потолка.
Как посчитать квадратуру стен?
Размер стены в квадратных метрах нужен для подсчёта количества отделочных материалов, размещения полок, зеркал или навесных шкафов.
Сплошная стена
Квадратура стены рассчитывается аналогично площади пола – длина, высота стены после обмера перемножаются между собой. Учитывают все впадины и выступы, если такие есть. Стены мансардных помещений под крышей часто ломаной формы, сегменты находятся в разных плоскостях.
В этом случае участки стены измеряют по отдельности, переносят на бумагу. Подсчитывают площадь каждой отдельной геометрической фигуры и суммируют числа.
С окном
Определяя количество квадратных метров стены, оконные проёмы, как правило, исключают.
Торцевые грани стен возле окна называют откосами, их размеры также не входят в метраж стены и считаются отдельно, например при подсчёте штукатурных работ или шпаклёвки.
С дверью
Квадратуру дверного проёма из площади стены при расчёте вычитают. Откосы при необходимости измеряют отдельно.
Измеряем площадь неправильной фигуры
Высчитывая метраж декоративных арочных проёмов или стрельчатых окон, поступают по тому же принципу, разбивая сложную фигуру на несколько простых элементов.
С квадратами и прямоугольниками совмещают части круга и треугольники.
Окружность
Целый круг в интерьере встречается достаточно редко. Полностью круглым может быть окно, колонны, центральная часть многоуровневого потолка. В основном дело приходится иметь с частями круга: половиной или сегментами.
Рулеткой снимают размер между двумя противоположными точками круга. Этот отрезок будет называться диаметром. Радиус круга равен половине диаметра.
Радиус круга равен половине диаметра.
Подсчёт площади круга производят по формуле S = π*R², где:
- R – радиус;
- S – площадь круга;
- π – постоянная математическая величина, округлённая до значения 3,14.
Числовое значение площади полукруга получают делением полученного результата на 2.
Квадратура сектора круга равна произведению половины длины дуги сектора на радиус круга, вычисляется по формуле S = 1/2 L*R.
Треугольник
Формула площади треугольника S=1/2*Н*А, где:
- S – площадь треугольника;
- Н – высота;
- А – сторона треугольника.
Высоту треугольника получают, измеряя рулеткой перпендикуляр от угла, противоположного к стороне.
Источник: https://DomaVlad.ru/sovety-dlya-doma/kak-poschitat-kvadratnye-metry.html
Как рассчитать квадратные метры стен комнаты, расчет площади стен
Приведу пример расчета пола и стен комнаты (кухни) в квадратных метрах.
Формула расчета простая, S = a*b, где S — площадь, а и b — соответственно, длина и ширина комнаты. В нашем примере (рисунка с обмерами) вместо маленьких букв длина — А и ширина — Б., и противоположенных стен — Г и В.
Чтобы рассчитать площадь комнаты по полу:
— если у нас длина комнаты 5 метра, а ширина 3 метров, тогда нам надо ( 5*3 = 15 кв.м.), в итоге получаем 15 кв.м. по полу
Чтобы рассчитать площадь комнаты по стенам:
Надо с начало сложить длины всех четырех сторон комнаты А + Б + Г + В и умножить на высоту потолка комнаты h, ( А + Б + Г + В)* h — если у нас длина комнаты 5 метра, а ширина 3 метров, а высота потолка комнаты к примеру 2,5 метра, тогда надо ((5+3+5+3)*2,5= 40 кв.м.), в итоге получаем 40 кв.м. по стенам.
- Но это еще не все, для того чтобы получить чистые квадратные метры стен комнаты для ремонта и отделки квартиры, надо из полученного вычесть двери и окно.

- К примеру:
— если у нас размеры окна ширина 1,6 метров, а высота 1,5 метров. — а двери ширина 0,8 метров, а высота 2,05 метров. Окно: (1,6*1,5)= 2,4 кв.м., в итоге окно получаем 2,4 кв.м., Двери: (0,8*2,05)= 1,64 кв.м, в итоге двери получаем 1,64 кв.м., Осталось вычесть от (40-2,4-1,64)= 35,96 кв.м.,
ИТОГО: Получили 35,96 кв.м. по стенам комнаты.
- Если вы не хотите в ручную рассчитывать площадь стен или вы, что то не поняли при описание расчетов, то вы можете воспользоваться нашим калькулятором и рассчитать площадь стен автоматически.
- Для расчёта необходимо измерить в метрах длину, ширину комнаты и высоту потолка и внести данные по порядку заполнив форму и вы автоматически получите расчет площади стен в квадратных метрах.
Калькулятор расчёта площади стен
Примечание:
Обращаем ваше внимание, что измерения необходимо проводить в метрах. Т.е. если вы получили длину комнаты 964 сантиметров, то в поля формы необходимо ввести значение 9.64. Обратите внимание, что дробные числа нужно вводить с точкой, а не с запятой!
Т.е. если вы получили длину комнаты 964 сантиметров, то в поля формы необходимо ввести значение 9.64. Обратите внимание, что дробные числа нужно вводить с точкой, а не с запятой!
Т.е. 2,6 — неправильно, 2.6 — правильно
Калькулятор рассчитывает только площадь стен, но без учета и вычета площади окон и дверей, для этого надо еще раз повторить расчеты на площадь окон и дверей описанные выше.
К примеру:
— если у нас размеры окна ширина 1,6 метров, а высота 1,5 метров. — а двери ширина 0,8 метров, а высота 2,05 метров. Окно: (1,6*1,5)= 2,4 кв.м., в итоге окно получаем 2,4 кв.м., Двери: (0,8*2,05)= 1,64 кв.м, в итоге двери получаем 1,64 кв.м.,
Осталось вычесть от (от полученных расчетов автоматического калькулятора (площадь чистых стен) -2,4-1,64 (Окно и двери)= получим площадь стен с учетом вычета Окон и двери помещения (комнаты) в кв.м.,
Чтобы рассчитать площадь комнаты по полу: воспользуйтесь нашим Калькулятором, чтобы расчитать площадь пола или потолка.
Калькулятор рассчитывает не только площадь пола или потолка, а также данный калькулятор можно использовать для расчёта площади любых других прямоугольных объектов у которых есть длина и ширина. В этом случае вместо ширины и длины комнаты вам необходимо подставить значения ширины и длины этих самых объектов (окна, двери и т.д.,) к примеру таких как площадь окон и дверей.
Источник: http://remont-otdelka-m.ru/kak-rachitaty-kvadratnie-metri.php
Квадратный метр это сколько: как измерить квадратуру комнаты самостоятельно — формулы в помощь
- При проведении ремонтных работ возникает вопрос: квадратный метр – это сколько необходимо материалов, чтобы его покрыть.
- Чтобы не потратить лишние деньги, лучше для начала произвести расчет квадратных метров комнаты и только потом отправляться в магазин с конкретными требованиями.
- На упаковках с красками, штукатуркой, грунтовкой обязательно обозначено, на какой размер помещения рассчитано данное количество смеси.

- Главный вопрос – сколько необходимо упаковок или банок, чтобы хватило на площадь стен или пола.
Что такое квадратный метр
Для начала надо определиться, что из себя представляет квадратный метр. Люди, которые плохо учили в школе математику, все равно рано или поздно сталкиваются с проблемой подсчета количества строительных материалов. Поэтому квадратный метр – основная точка отсчета при определении площади помещения.
Если нарисовать квадрат (это геометрическая фигура с одинаковыми сторонами), и сторона будет равна 100 см, то при умножении на 100 получим число 10000 см. это означает, что размер данной фигуры 10000 см2. Можно проще. Посчитать в метрах: 100 см – это 1 м. Применяем формулу подсчета площади – перемножаем две стороны, то есть 1 умножаем на 1, получаем 1 м. Значит, размер квадрата 1 кв.м.
Инструменты для подсчета квадратных метров
Для вычислений необходимо подготовить калькулятор.
com/embed/VmciATFAhuQ?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>
Если его нет, тогда таблицу умножения на обычной тетради для первоклассника.
Если стены имеют не 2, не 3 метра, а, например 2,5 метра, то лучше все-таки калькулятор. Это чересчур сложная нагрузка для мозга, который не привык работать с цифрами.
Формула подсчета квадратных метров
Чтобы рассчитать площадь, необходимо применить формулу квадратного метра А X B, где число А – это длина одной стороны, а число В – длина второй стороны. Они могут быть одинаковы, если форма пола или стены квадратная.
Чаще всего она не квадратная, а прямоугольная, то есть число А будет иметь одно значение, а число В – другое. Их необходимо будет перемножить в уме, или по таблице умножения, или на калькуляторе. И полученное число будет площадью, которую надо будет покрывать краской или еще чем-нибудь.
Это интересно! Иногда нужно знать как правильно высчитываются размеры. Сколько же 1 4 дюйма в мм? Об этом можно прочесть в нашей статье.
Сколько же 1 4 дюйма в мм? Об этом можно прочесть в нашей статье.
Бывает, что форма пола не стандартная, а, например, трапециевидная. Тогда сложнее, особенно тем людям, кто не знает, что такое треугольник (такое тоже есть в природе).
Чтобы рассчитать размер трапеции, необходимо посчитать сначала площадь прямоугольника в середине, потом величину каждого треугольника по бокам, потом эти три числа сложить.
Не легче ли сразу позвать бригаду рабочих? Пускай они думают, как рассчитать квадратные метры комнаты.
Важно! Если на этом этапе возникло непонимание, то лучше сразу позвать учителя математики и попросить подсчитать, сколько кв. метров имеет комната.
Площадь пола или потолка
Потолка и пол в обычной квартире одинаковые. Как посчитать квадратные метры? Очень просто. Если помещение мансардное, тогда потолка там нет – есть только пол и стены.
Этап № 1. Измерить длину комнаты и записать полученное число на бумаге. Если число целое, тогда пишем просто цифру. Например, 5 (м). Если число больше 5, но меньше 6, тогда придется вспомнить десятичные дроби и написать, к примеру, 5,5 (м).
Если число целое, тогда пишем просто цифру. Например, 5 (м). Если число больше 5, но меньше 6, тогда придется вспомнить десятичные дроби и написать, к примеру, 5,5 (м).
Этап № 2. Измерить ширину комнаты и записать аналогично. К примеру – 3м.
Этап № 3. Теперь необходимо перемножить эти два числа. Пример: 5 x 3 = 15м. Итак, площадь пола – 15 кв. м. Следовательно, размер потолка также будет равняться 15 кв. м. Записать это число отдельно и обвести ручкой.
Площадь сплошной стены
Как вычислить квадратуру сплошной стены? Так же, как мы измеряли пол или потолок. Алгоритм действий тот же, что и при подсчете размера пола:
- измерить длину стены и записать;
- измерить высоту;
- перемножить два числа – полученный результат и будет площадью в квадратных метрах.
Пример: высота 2,20 м, длина 7м. 7 x 2,2 = 15,4 м. Площадь стены – 15,4 кв. м.
Как посчитать квадратные метры стены с окном
Сложнее будет иметь дело со стеной, на которой расположено окно.
В таком случае надо отдельно высчитать размер стены, отдельно – размер окна. Потом из большей площади вычесть меньшую. Получится число метров квадратных, которое необходимо будет покрыть краской или штукатуркой.
Алгоритм действий:
- По уже пройденному сценарию высчитать размер стены. Пускай будет уже известное число – 15,4 м2.
- Далее измерить высоту и длину окна. Перемножить числа. К примеру: длина 1,5 м, высота 1,2 м. Если умножить, то получится 1,8. Значит, площадь окна 1,8 кв. м.
- Берем площадь стены и вычитаем из нее размер окна: 15,4 – 1,8 = 13,6. Площадь, которую необходимо будет привести в порядок, – 13,6 кв. м.
Важно! Цифры, которые получаются при подсчетах, обязательно записывать и обводить ручкой, чтобы не потеряться в собственных расчетах.
Как посчитать квадратные метры стены с дверью
Похожие действия необходимо производить, когда требуется высчитать квадратные метры стены с дверью. Если дверь с математической точки зрения простой прямоугольник, то вычисляем ее площадь по обычной формуле А X В. То есть надо измерить высоту и длину, далее числа перемножить и получится размер двери.
То есть надо измерить высоту и длину, далее числа перемножить и получится размер двери.
Далее из площади стены вычитаем размер двери и получаем квадратуру, на которую необходимо будет покупать отделочные материалы. Если предыдущий хозяин квартиры сделал дверь с аркой, то здесь без вычисления размера круга никак не обойтись.
Измеряем площадь сложных фигур
Круг и треугольник – сложные фигуры для самостоятельного вычисления. Как измерить квадратные метры окружности, если нет математического или инженерного образования? Опять-таки по формуле.
Как измерить размер окружности
Существует формула вычисления площади круга. Есть такое постоянное число – отношение длины окружности к ее диаметру. Оно одинаково для всех размеров круга. Называется оно пи и равняется 3,14. Вот это число и используют при подсчетах.
Этап № 1. Замеряем диаметр (это линия, которая проходит через центр круга от одного края окружности к другому). Пускай диаметр будет равняться 3 м.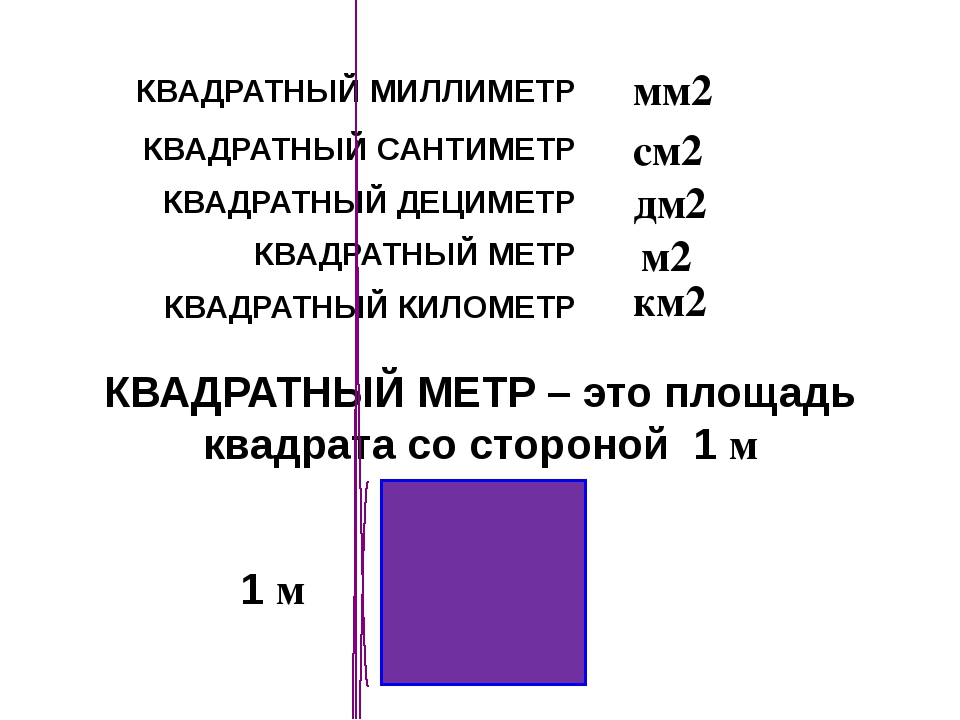 Далее находим радиус – это половина длины диаметра. То есть 1,5 м. Записываем радиус на бумагу.
Далее находим радиус – это половина длины диаметра. То есть 1,5 м. Записываем радиус на бумагу.
Этап № 2. Производим расчеты по формуле S = ПR2, где S – это площадь круга, П – постоянное число, а R – радиус окружности. Получается 3,14 x (1,5 x 1,5) = 7, 065. Площадь данного круга – 7,065 кв. м.
Но это площадь целого круга. Арка над дверью – это половина круга. Значит, еще нужно разделить данное число на два и далее прибавить к прямоугольной площади двери. 7,065 : 2 = 3,53 м2.
Как измерить площадь треугольника
Если предыдущий хозяин квартиры был математик, то он вполне мог сделать на потолке треугольные фигуры, которые приходится реставрировать и выделять другим цветом или штукатуркой. Придется считать, чтобы не переплачивать.
Расчет метра квадратного в треугольной фигуре начинается с внимательного осмотра этой фигуры.
Необходимо найти основание треугольника, то есть линию, на которую опираются две других (как крыша на доме). Далее провести линию из противоположной верхушки к основанию. Эти два числа записать.
Эти два числа записать.
Этап № 1. Разделить основание треугольника на 2 и записать. Это число пригодится в недалеком будущем. Измерить высоту и тоже записать.
Этап № 2. Произвести расчет м2 фигуры. Для этого необходимо использовать формулу: S = 0,5аh, где S – площадь треугольника, а – основание, а h – высота. Пример: основание 3 м, высота 2,5 м. Итого: 0,5 x 3 x 2,5 = 3,75. Размер треугольника – 3,75 м2. Записать, чтобы не забыть.
Советы и рекомендации
Таким образом можно высчитать площадь всей квартиры и расписать, что и каким цветом красить. Размеры всех стен и потолка сложить – получится число, на которое надо будет ориентироваться при покупке стройматериалов.
Совет! При расчетах лучше пригласить еще одного человека в помощь. Одна голова хорошо, а две надежнее.
Дело за малым – пойти в магазин и купить материалы. Здесь еще придется считать, так как не все упаковки предназначены для больших помещений. К примеру, размер потолка на кухне 3 x 3. Сколько квадратных метров штукатурки понадобится, если одной упаковкой можно покрыть 3 кв. м? Считаем: размер потолка 9 кв. м. Одна упаковка уходит на 3 кв. м. Следовательно, на весь потолок необходимо 3 пачки.
Сколько квадратных метров штукатурки понадобится, если одной упаковкой можно покрыть 3 кв. м? Считаем: размер потолка 9 кв. м. Одна упаковка уходит на 3 кв. м. Следовательно, на весь потолок необходимо 3 пачки.
Если на упаковке написано, что расход на 12 квадратных метров, это означает, сколько материала надо, чтобы покрыть стену размером 3 x 4 м.
Или другой пример. Стена в квартире 6 на 4. Сколько квадратных метров необходимо закрасить? Умножаем 6 на 4, получаем 24 квадратных метра. Это сколько нужно банок краски по 3 л, если каждая банка расходуется на 6 кв. м? Считаем: 24 делим на 6. Получается 4. Значит, необходимо купить 4 трехлитровых банки краски для покрытия всей стены.
Для ремонтных работ всегда лучше взять немного больше материалов, чтобы потом не идти лишний раз в магазин. В будущем, если придется что-то подкрасить или подбелить, остатки материалов могут здорово выручить.
Источник: https://stroim.guru/polezno-znat/kvadratnyj-metr-eto-skolko. html
html
Сколько метров в сотке, как перевести сотки в квадратные метры + КАЛЬКУЛЯТОР
Главная » Разное » Сколько квадратных метров в сотке земли: измерение, расчёт
Если вы затрудняетесь выяснить, сколько метров в сотке, или не знаете, как перевести сотки в квадратные метры, то после прочтения этой статьи вы точно будете знать, как это сделать.
Размер одной сотки земли равен 100 м2
Максимально кратко и ёмко разберём, что такое земельная сотка, каковы её величины в разных единицах измерения (гектары/ар). От слов перейдём к делу – посчитаем размеры на примерах конкретных участков.
Содержание статьи
Откуда взялись сотки – устраним путаницу в понятиях
В дореволюционной России классической величиной измерения земли служила десятина, которая подразделялась на фиксированные единицы измерения. Например, «бахчевая» с размером участка 80х10 м2 (саженей в старину).
При помощи десятин измеряли даже площадь для покоса травы, делая нехитрый расчёт: десятина земли – 10 стогов сена. Эта единица измерения использовалась вплоть до революции 1917 года, через год после которой страна начала постепенный переход на метрическую систему мер.
Эта единица измерения использовалась вплоть до революции 1917 года, через год после которой страна начала постепенный переход на метрическую систему мер.
Понятие десятины заменил ар – квадратный участок земли 10х10 м, что соответствует 100 м2. Новая мера заметно облегчила сложность подсчётов, поскольку общую площадь стало легко измерять по числу квадратов 10х10 м, входящих в конкретный участок.
Дачный участок в 6 соток
Сотки, как название, появились ещё в советские годы, когда стали массово появляться дачи, площадь которых укладывалась в 4–6 аров. «Сотка» буквально означает числительное «сто», легко произносится и не вызывает путаницы с количеством метров.
Так народное определение уверенно заняло своё место в языке советских граждан и успешно прижилось в современности. Однако вопросы вроде «сколько квадратных метров в одной сотке» до сих пор актуальны.
Особенно сложно разобраться в вопросе тем, кто никогда не сталкивался с необходимостью измерить площадь участка, чтобы понять его реальные размеры (например, при покупке/продаже земли).
Вы удивитесь, насколько всё просто: 1 сотка – это 100 квадратных метров или ар земли, а площадь в 10 соток соответствует 10х100 м2. Зная метраж сотки, теперь вы легко можете планировать строительство – на сколько квадратов можно построить дом, сколько отвести для других построек, а сколько достанется грядке с клубникой.
При этом большие территории (сельского назначения, аренда лесных участков и т. д.) измеряют в гектарах. Наравне с квадратными метрами эту единицу измерения используют кадастровые инженеры, вычисляя площадь объектов. Поэтому навык переводить метры в сотки и в гектары пригодится каждому грамотному человеку.
Единицы измерения площади земельных наделов
Есть ещё одна единица измерения больших участков земли — акр. В нашей стране ей пользуются для определения площади земельных угодий сельскохозяйственного назначения. Один акр земли это 4046,86 м² или 40,47 соток.
Как узнать, сколько соток на участке
Сколько метров в аре мы выяснили, поэтому от теории – к практике. Чтобы перевести это значение в квадратные метры, вспоминаем вместимость 1 сотки – это 100 м2. Для визуального представления площади земли в сотке, измеряем ее в метрах и получаем нужное число.
Чтобы перевести это значение в квадратные метры, вспоминаем вместимость 1 сотки – это 100 м2. Для визуального представления площади земли в сотке, измеряем ее в метрах и получаем нужное число.
Предположим, вы провели замер территории рулеткой и выяснили расстояние по каждой из сторон: длина участка составила 65 метров, а ширина 40 метров. Чтобы посчитать общую площадь, остаётся перемножить полученные цифры: 65х40 = 2600 квадратных метров.
Теперь переводим метры в сотки. Для этого земельную площадь в метрах делим на количество метров в 1 сотке: 2600/100 = 26 соток. Аналогичный алгоритм действий проводим в обратном порядке, если сотки необходимо перевести в метры. Буквально: 40 соток х 100 м = 4000 м2.
Для вычисления в гектарах используют аналогичный принцип, только метры делят на 10 000, поскольку 1 гектар равен 10 тысячам квадратных метров. Проще всего выяснить площадь участка в виде прямоугольника или квадрата, обладающего правильной формой.
Сложнее посчитать участок в виде многоугольника, где техника расчётов заметно меняется. В этом случае отрезок земли делят на несколько треугольников, считают размер каждого и складывают между собой, получая общий метраж участка.
В этом случае отрезок земли делят на несколько треугольников, считают размер каждого и складывают между собой, получая общий метраж участка.
На практике встречаются земельные участки совершенно разных форм – от многоугольника и трапеции до круга и треугольника. Поэтому для точности расчёта нестандартных наделов важно обратиться к профильным специалистам – кадастровым инженерам, в расчёте которых будет учтён каждый сантиметр ваших владений.
Сколько соток на участке – расчёт на примере
Проведём вычисление для участка прямоугольной формы с переводом в сотки:
- Отмечаем углы участка, вбивая небольшой колышек (можете хоть камень положить – главное, визуально обозначить угловую часть).
- Измеряем длину и ширину используя подручные инструменты – рулетку или палку длинной 1 метр.
- Умножаем длину участка на его ширину. Допустим, ваш «прямоугольник» составил 36 м. в длину, 24 м. в ширину. Перемножив показатели, вы получите размеры в квадратных метрах, то есть 864 м2.
 Следует отметить, что не нужно путать вычисление площади участка с его периметром. Вычисляя периметр, можно найти общую длину сторон, а не площадь.
Следует отметить, что не нужно путать вычисление площади участка с его периметром. Вычисляя периметр, можно найти общую длину сторон, а не площадь. - Переводим метры в сотки. Вспоминаем, сколько метров в сотке – 100 м2. Соответственно, 864 / 100 = 8.64 сотки.
Перевести сотки в метры можно умножением (8.64х100 = 864).
Ответы на частые вопросы:
- 10 соток – это сколько м2? Умножайте 10 на 100 и получите верный ответ: в 10 сотках – 1000 м2.
- 6 соток – это сколько квадратных метров? Проводим аналогичное вычисление и получаем 600 м2.
- 1000 м2 – сколько соток? 1 тысячу метров делим на 1 сотку, то есть 1000/100, и получаем ответ: 10 соток.
Таблица перевода метров квадратных в сотки:
| М2 | 100 | 200 | 300 | 400 | 600 | 900 | 1 000 | 1200 | 2 500 |
| сотки | 1 | 2 | 3 | 4 | 6 | 9 | 10 | 12 | 25 |
Главное в расчётах – не забывать о переводе больших единиц в меньшие, чтобы получить верный размер земельного отрезка.
Сколько соток в 1 га
Измерять большие территории принято гектарами – это удобно и практично. Напомним, что 1 га соответствует 100 соткам, которые составляет 10 000 м2. Все официальные документы, содержащие сведения о площади территорий больше 100 соток (например, фермерские земли), зарегистрированы в гектарах.
Размер в сотках одного гектара
Обратите внимание, что размеры таких земель исчисляются квадратными километрами. Сколько это составит в сотках? Первым делом переводим площадь 1 км2 в метры. Пример: 1000 м х 1000 м = 1 000 000 м2. Полученная цифра соответствует 100 га или 10 000 соток.
Участок нестандартной формы – как вычислить количество соток
При замерах важно считать точно по границам участка. Особенно если расчёт готовят для оформления документов на землю.
Существует 3 способа узнать количество соток для участка неправильной формы:
- Провести межевание. Пригласите на замеры специалиста, который определит площадь геодезическим методом, используя дальномеры, специальную вышку и другие приборы.
 Это максимально достоверный способ узнать размеры участка: неправильная форма будет разбита на несколько равных треугольников, подсчитана их площадь по отдельности и в сумме. Результат – точное количество соток, включая самые неудобные для «ручных» замеров места.
Это максимально достоверный способ узнать размеры участка: неправильная форма будет разбита на несколько равных треугольников, подсчитана их площадь по отдельности и в сумме. Результат – точное количество соток, включая самые неудобные для «ручных» замеров места. - Измерить самостоятельно. Для этого установите вехи по углам всего периметра, затем проведите замер расстояния между каждой из них. Зафиксируйте схему участка и полученные цифры на бумаге. Разделите землю на схеме, на отдельные фигуры с правильной геометрией. Посчитайте площадь каждой в отдельности, а полученные результаты сложите – итоговая цифра покажет общее количество соток.
- Используйте Google-карту. Подходит в качестве способа вычислить приблизительные размеры для общей информации. В удалённом расчёте по карте можно выставить точки по всем границам территории, соединить и получить готовый результат.
На картах в Google maps можно различить границы участков
Размер геометрически сложных земель подручными средствами определить сложно, поскольку погрешности будут неизбежны. Если вы проводите расчёт для оформления документов, используйте услуги профильных компаний – это требует денег, но даёт гарантию точности в измерении границ и площади участка.
Если вы проводите расчёт для оформления документов, используйте услуги профильных компаний – это требует денег, но даёт гарантию точности в измерении границ и площади участка.
— Сайт калькулятора
Используйте этот конвертер площади для мгновенного преобразования акров, квадратных сантиметров, квадратных футов, квадратных миль и других метрических и британских единиц площади.
Единицы преобразования для конвертера площади
Акры (ac), Арес (a), Сараи (b), Центы (ct), Гектары (га), Пинг, Квадратные Ангстремы, Квадратные астрономические единицы, Квадратные сантиметры (см 2 ), Квадратные дециметры (дм 2 ) ), Квадратные декаметры (плотина 2 ), квадратные сажени, квадратные футы ( 2 футов), квадратные гектометры (hm 2 ), квадратные дюймы ( 2 ), квадратные километры ( 2 км), Квадратные световые годы, квадратные метры (м 2 ), квадратные микрометры (мкм 2 ), квадратные микроны, квадратные мили (mi 2 ), квадратные миллиметры ( 2 мм), квадратные миллимикроны, квадратные нанометры (нм ) 2 ), квадратные парсеки, квадратные стержни, квадратные ярды (ярды 2 ),
Если вы хотите рассчитать площадь в квадратных футах для комнаты или участка для пола, озеленения, ковров или плитки, воспользуйтесь калькулятором квадратных футов.
Популярные индивидуальные конвертеры:
центов и акров, Гектары и акры, Квадратные дюймы и квадратные сантиметры, Квадратные футы и акры, Квадратные футы и центы, Квадратные футы и гектары, Квадратные километры и акры, Квадратные километры и гектары, Квадратные метры и сотки, Квадратные метры в Квадратные дюймы, Квадратные метры в Квадратные футы, Квадратные метры и центы, Квадратные стержни в квадратные футы,
Определения преобразователя площади
Акров
Акр — это единица площади в британской системе мер и единиц.С. Обычные системы. Акр часто используется для измерения площадей земли и ее площади. международный символ — ac . Вы можете узнать больше об акрах в статье, сколько это акр?
А
Площадь составляет 100 квадратных метров (10 х 10 м). Обычно он используется для измерения земельной площади. Хотя в настоящее время считается, что Аре не входит в современную международную систему (СИ), он все еще используется для
измерить недвижимость в некоторых странах Европы. Его международный символ — a .
Его международный символ — a .
Га
Гектар — это единица площади, равная 10 000 квадратных метров (107 639 квадратных футов) или одному квадратному гектометру (100 м x 100 м), и обычно используется для измерения площади земли. Он чаще всего используется в геодезической профессии для повседневных юридических документов, таких как земельные документы, ипотечные исследования, градостроительство, экология. защита и другие необходимые имущественные соображения в соответствии с законом. Подробнее о гектарах читайте в статье, а какой гектар?
Чтобы повысить продуктивность, мы теперь устанавливаем cookie для хранения последних единиц, из которых и в которые вы конвертировали.Это означает, что при повторном посещении этого конвертера площади единицы измерения будут выбраны автоматически.
Конвертер квадратных метров и акров (м² и акров)
Добавить в телефон
Используйте этот калькулятор для конвертации квадратные метры (м²) в акры (акры) и акры в квадратные метры. Этот конвертер является частью полной
инструмент для преобразования площади.
Этот конвертер является частью полной
инструмент для преобразования площади.Нравится? Поделитесь, пожалуйста,
Пожалуйста, помогите мне распространить информацию, поделившись этим с друзьями или на своем веб-сайте / в блоге.Спасибо.
Связь
Заявление об ограничении ответственности: Несмотря на то, что для создания этого калькулятора были приложены все усилия, мы не можем несет ответственность за любой ущерб или денежные убытки, возникшие в результате или в связи с его использованием. Этот инструмент предназначен исключительно в качестве услуги для вас, пожалуйста, используйте его на свой страх и риск. Полный отказ от ответственности. Не используйте расчеты для чего-либо, где неточные расчеты могут привести к гибели людей, деньгам, имуществу и т. Д.
Пересчет акров и квадратных метров
В приведенных ниже таблицах преобразования цифры округлены максимум до 5 десятичных знаков (7 с меньшими числами), чтобы дать приблизительные значения.
| Акров | Квадратные метры |
|---|---|
| 1 акр | 4046.85642 кв.м |
| 2 сотки | 8093.71284 кв. М |
| 3 сотки | 12140.56927 квадратных метров |
| 4 сотки | 16187.42569 кв.м |
| 5 соток | 20234.28211 квадратных метров |
| 6 соток | 24281.13853 кв.м |
| 7 соток | 28327.99496 кв.м |
| 8 соток | 32374.85138 кв.м |
| 9 соток | 36421.7078 квадратных метров |
| 10 соток | 40468.56422 квадратных метров |
| 11 соток | 44515.42065 кв.м |
| 12 соток | 48562.27707 кв.м |
| 13 соток | 52609.13349 квадратных метров |
| 14 соток | 56655.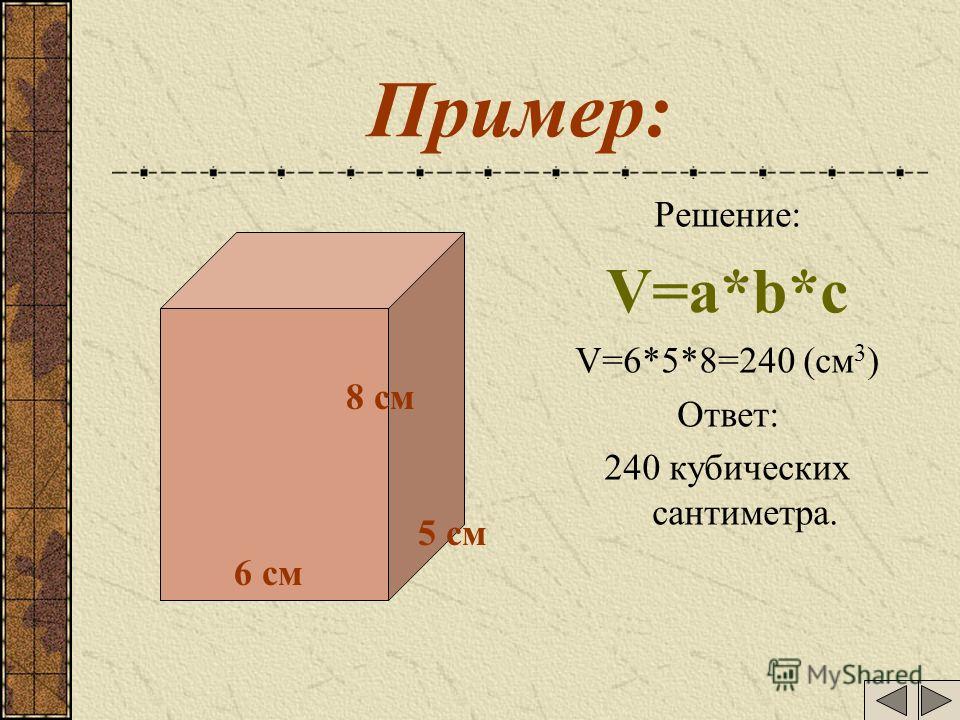 98991 кв.м 98991 кв.м |
| 15 соток | 60702.84634 кв.м |
| 16 соток | 64749.70276 кв.м |
| 17 соток | 68796.55918 кв.м |
| 18 соток | 72843.4156 кв.м |
| 19 соток | 76890.27203 кв.м |
| 20 соток | 80937.12845 квадратных метров |
| Квадратные метры | соток |
|---|---|
| 1 квадратный метр | 0.00025 соток |
| 2 квадратных метра | 0,00049 соток |
| 3 квадратных метра | 0,00074 соток |
| 4 квадратных метра | 0,00099 соток |
| 5 квадратных метров | 0,00124 соток |
| 6 квадратных метров | 0,00148 соток |
| 7 квадратных метров | 0,00173 соток |
| 8 квадратных метров | 0.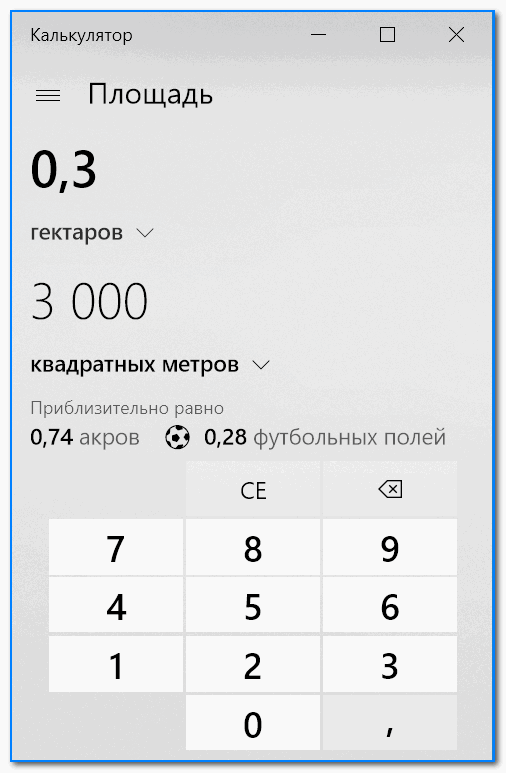 00198 соток 00198 соток |
| 9 квадратных метров | 0,00222 соток |
| 10 квадратных метров | 0,00247 соток |
| 11 квадратных метров | 0,00272 соток |
| 12 квадратных метров | 0,00297 соток |
| 13 квадратных метров | 0,00321 соток |
| 14 квадратных метров | 0,00346 соток |
| 15 квадратных метров | 0.00371 соток |
| 16 квадратных метров | 0,00395 соток |
| 17 квадратных метров | 0,0042 соток |
| 18 квадратных метров | 0,00445 соток |
| 19 квадратных метров | 0,0047 соток |
| 20 квадратных метров | 0,00494 соток |
Сколько квадратных метров в 1 акре?
В 1 акре 4046,8564224 квадратных метра.Чтобы преобразовать из акров в квадратные метры,
умножьте свою цифру на 4046,8564224 (или разделите на 0,00024710538146717).
Сколько гектаров в 1 квадратном метре?
В 1 м.кв. 0,00024710538146717 соток. Чтобы преобразовать квадратные метры в акры, умножьте свою цифру на 0,00024710538146717 (или разделите на 4046,8564224).
РекламаЧто такое акр?
акра — это единица земли, обычно используемая в Северной Америке и Карибском бассейне.Он равен 4 047 кв. М или 43 560 кв. Футов. Это примерно равно 40 процентам гектара. Интересно, что корни этого акра восходят к средневековью. Он был определен как площадь, которую можно было вспахать за один день с помощью быка. Один акр составляет примерно 76 процентов от размера футбольного поля. Многие пригородные участки имеют размер от четверти до одной пятой акра. Вы можете узнать больше об акрах в статье, сколько это акр?
Что такое квадратный метр?
Иначе сокращенно m 2 , квадратных метра (или «метр» в британском написании) — это квадрат, у которого равные стороны равны одному метру. Его часто используют для измерения площади помещения или общей площади внешнего участка земли. Квадратный метр равен 10 000 квадратных сантиметров, 10,76 квадратных футов и 0,0001 га. Большие эркеры иногда равняются квадратному метру. Ковровые покрытия и деревянные полы также оцениваются за квадратный метр.
Его часто используют для измерения площади помещения или общей площади внешнего участка земли. Квадратный метр равен 10 000 квадратных сантиметров, 10,76 квадратных футов и 0,0001 га. Большие эркеры иногда равняются квадратному метру. Ковровые покрытия и деревянные полы также оцениваются за квадратный метр.
Прочие преобразователи индивидуальных площадей
Ары и акры, Центы и акры, Гектары и акры, Квадратные сантиметры и акры, Квадратные футы и акры, Квадратные дюймы и акры, Квадратные километры и акры, Квадратные метры и акры, Квадратные метры и акры, Квадратные Метры и центы, квадратные метры и гектары, квадратные метры и квадратные сантиметры, квадратные метры и квадратные дециметры, квадратные метры и квадратные декаметры, квадратные метры и квадратные футы, квадратные метры и квадратные гектометры, квадратные метры и квадратные дюймы, квадратные метры и квадратные километры , Квадратные мили и акры, квадратные мили и квадратные метры, квадратные миллиметры и квадратные метры, квадратные стержни и акры, квадратные ярды и акры, квадратные ярды и квадратные метры,
Конвертер квадратных футов и центов (ft² и ct)
Добавить в телефон
Используйте этот калькулятор для конвертации квадратные футы (ft²) в центы (ct) и центы в квадратные футы.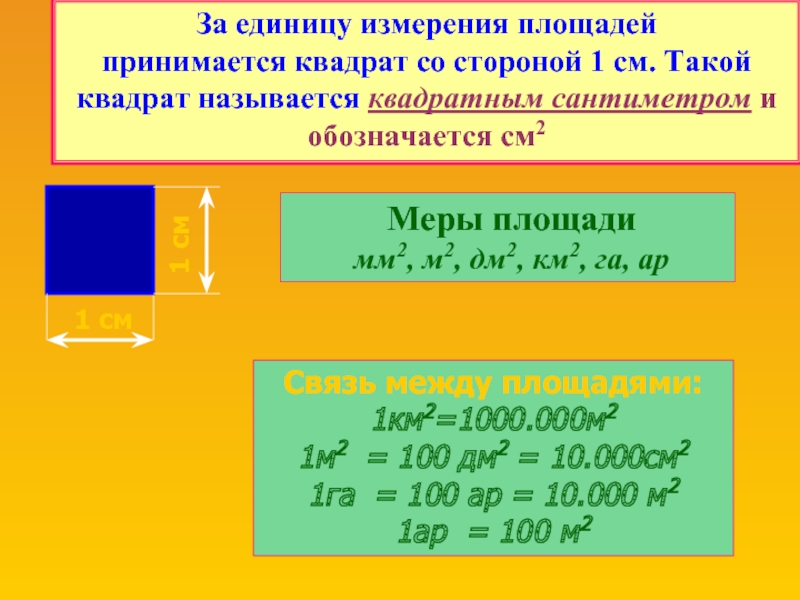 Этот конвертер является частью полной
инструмент для преобразования площади.
Этот конвертер является частью полной
инструмент для преобразования площади.Нравится? Поделитесь, пожалуйста,
Пожалуйста, помогите мне распространить информацию, поделившись этим с друзьями или на своем веб-сайте / в блоге. Спасибо.
Связь
Заявление об ограничении ответственности: Несмотря на то, что для создания этого калькулятора были приложены все усилия, мы не можем несет ответственность за любой ущерб или денежные убытки, возникшие в результате или в связи с его использованием.Этот инструмент предназначен исключительно в качестве услуги для вас, пожалуйста, используйте его на свой страх и риск. Полный отказ от ответственности. Не используйте расчеты для чего-либо, где неточные расчеты могут привести к гибели людей, деньгам, имуществу и т. Д.
Преобразование центов и квадратных футов
В приведенных ниже таблицах преобразования цифры округлены максимум до 5 десятичных знаков (7 с меньшими числами), чтобы дать приблизительные значения.
| центов | Квадратные ноги |
|---|---|
| 1 цент | 435.6 квадратных футов |
| 2 цента | 871,2 квадратных футов |
| 3 цента | 1306,8 квадратных футов |
| 4 цента | 1742,4 квадратных футов |
| 5 центов | 2178 квадратных футов |
| 6 центов | 2613,6 квадратных футов |
| 7 центов | 3049,2 квадратных футов |
| 8 центов | 3484,8 квадратных футов |
| 9 центов | 3920.4 квадратных фута |
| 10 центов | 4356 квадратных футов |
| 11 центов | 4791,6 квадратных футов |
| 12 центов | 5227,2 квадратных футов |
| 13 центов | 5662,8 квадратных футов |
| 14 центов | 6098,4 квадратных футов |
| 15 центов | 6534 квадратных футов |
| 16 центов | 6969,6 квадратных футов |
| 17 центов | 7405. 2 квадратных фута 2 квадратных фута |
| 18 центов | 7840,8 квадратных футов |
| 19 центов | 8276,4 квадратных футов |
| 20 центов | 8712 квадратных футов |
| Квадратные ноги | центов |
|---|---|
| 1 квадратный фут | 0,0023 цента |
| 2 квадратных фута | 0.00459 центов |
| 3 квадратных фута | 0,00689 центов |
| 4 квадратных фута | 0,00918 центов |
| 5 квадратных футов | 0,01148 центов |
| 6 квадратных футов | 0,01377 центов |
| 7 квадратных футов | 0,01607 центов |
| 8 квадратных футов | 0,01837 центов |
| 9 квадратных футов | 0,02066 центов |
| 10 квадратных футов | 0. 02296 центов 02296 центов |
| 11 квадратных футов | 0,02525 центов |
| 12 квадратных футов | 0,02755 центов |
| 13 квадратных футов | 0,02984 центов |
| 14 квадратных футов | 0,03214 центов |
| 15 квадратных футов | 0,03444 центов |
| 16 квадратных футов | 0,03673 центов |
| 17 квадратных футов | 0,03903 центов |
| 18 квадратных футов | 0.04132 центов |
| 19 квадратных футов | 0,04362 центов |
| 20 квадратных футов | 0,04591 цент |
Сколько квадратных футов в 1 центе?
В 1 ц. Чтобы преобразовать центы в квадратные футы, умножьте свою цифру на 435,6 (или разделите на 0,0022956841138659).
Сколько центов в 1 квадратном футе?
Есть 0.0022956841138659 центов за 1 квадратный фут. Чтобы преобразовать квадратные футы в центы,
умножьте свою цифру на 0,0022956841138659 (или разделите на 435,6).
Чтобы преобразовать квадратные футы в центы,
умножьте свою цифру на 0,0022956841138659 (или разделите на 435,6).
Прочие преобразователи отдельных площадей
Центы и акры, Центы и ары, Гектары и центы, Квадратные сантиметры и центы, Квадратные футы и акры, Квадратные футы и центы, Квадратные футы и гектары, Квадратные футы и квадратные сантиметры, Квадратные футы и квадратные дециметры , Квадратные дюймы и квадратные футы, квадратные километры и центы, квадратные километры и квадратные футы, квадратные метры и центы, квадратные метры и квадратные футы, квадратные мили и квадратные футы, квадратные миллиметры и центы, квадратные миллиметры и квадратные футы, квадратные стержни и квадрат Футы, квадратные ярды и центы, квадратные ярды и квадратные футы,
пожаловаться на это объявление пожаловаться на это объявлениеКалькулятор преобразования площади
Использование калькулятора
Преобразуйте единицы площади, введя значение для преобразования, а также от и до единиц.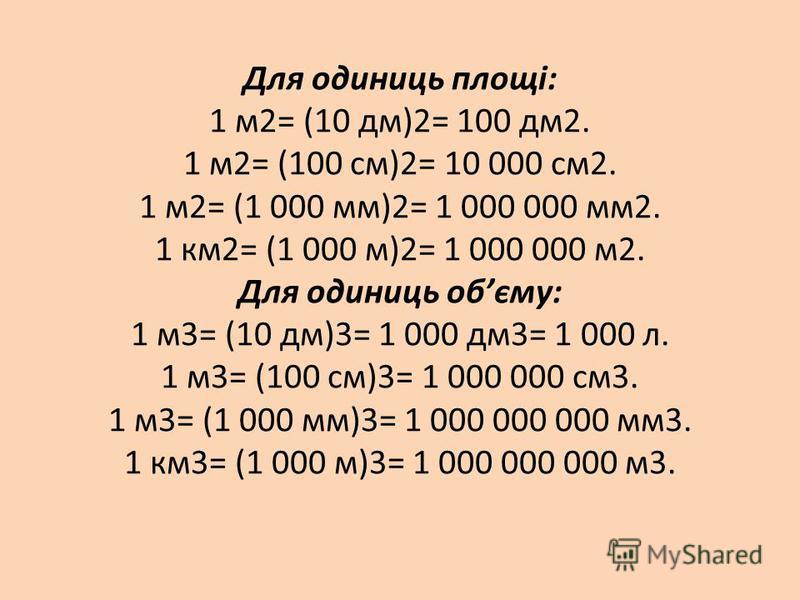
Как преобразовать единицы площади
Преобразования выполняются с использованием коэффициента преобразования. Зная коэффициент преобразования, преобразование единиц может стать простой задачей умножения:
S * C = E
Где S — наше начальное значение, C — наш коэффициент пересчета, и E — это наш конечный результат преобразования.
Чтобы просто преобразовать из любых единиц в м 2 , например, из 50 футов 2 , просто умножьте на значение в правом столбце в таблице ниже.
50 футов 2 * 0,092
[м 2 / фут 2 ] = 4,645152 м 2 Для преобразования 2 из m обратно в единицы в левом столбце разделите на значение в правом столбце или, умножив на обратную величину, 1 / x.
4.645152 м 2 /0.092
[м 2 / фут 2 ] = 50 футов 2 Для преобразования любых единиц в левом столбце, скажем, из A в B, вы можете умножить на коэффициент A, чтобы преобразовать A в m 2 , а затем разделить на коэффициент B для преобразования из m 2 . Или вы можете найти единственный фактор, который вам нужен, разделив фактор A на фактор B.
Например, чтобы преобразовать 2 футов в 2 , нужно умножить на 0.092
затем разделите на 0,000001. Или умножьте на 0,092 / 0,000001 = 92903,04. Таким образом, для прямого преобразования из 2 футов в 2 вы умножаете на 92903,04. Чтобы понять, как также преобразовать единицы, следуйте этому примеру. Допустим, вы хотите преобразовать из 2 футов в 2 метров.
Поскольку вы можете умножить что угодно на 1 и при этом сохранить исходное значение, но в других единицах, настройте его так, чтобы ft компенсировались, оставив вас с m.
С:
1 м = 3,28084 фута, 1 м / 3,28084 фута = 1Мы можем записать преобразование как:
1 фут 2 = 1 фут 2 * (1 м / 3,28084 фута) * (1 м / 3,28084 фута) = 0,0929030 м 2И теперь у нас есть коэффициент для преобразования 2 футов в 2 м, так как 1 * 0.0929030 = 0,0929030. Обратите внимание, что в этом значении есть ошибки округления. Значение в таблице 0,092
является более точным. Зная, что 1 фут 2 = 0,092
м 2 , теперь мы можем найти коэффициент преобразования для обратного преобразования. Разделив обе части уравнения на 0,092
, мы получим примерно 10,7639104 фута 2 = 1 м 2 . Таким образом, коэффициент преобразования, на который нужно умножить, чтобы преобразовать из 2 м в 2 футов, составляет около 10.7639104. Единицы, символы и значения преобразования
используется в калькуляторе этой площадиквадратный дюйм
в 2
кв.м.
0,00064516
квадратных футов
фут 2
кв.м.
0.092
кв.
Двор
ярд 2
кв.м.
0,83612736
квадратных миль
миль 2
кв.м.
2589988.110336
акров
ac
кв.м.
4046. 8564224
га
га
кв.м.
10000
квадратный миллиметр
мм 2
кв.м.
0.
000001
квадратный сантиметр
см 2
кв.м.
0,0001
кв. Км
км 2
кв.м.
1000000
Ссылки / Дополнительная литература
Национальный институт стандартов и технологий (NIST) — Руководство NIST по использованию Международной системы единиц — Приложение B, подразделы Б.8 факторов для единиц, перечисленных в алфавитном порядке и B.9 Факторы для единиц, перечисленных по виду количества или области науки.
Лиде, Дэвид Р.
, Дэниел (главный редактор). CRC Handbook of Chemistry and Physics, 89th Edition New York, NY: CRC Press, p. 1-28, 2008.
авторов Википедии. «Преобразование единиц» Википедия, Бесплатная энциклопедия. Википедия, Бесплатная энциклопедия, последний раз посещалась 26 июня.2011 г.
Арес в квадратные метры Преобразование (а в квадратный метр)
Введите площадь в ар ниже, чтобы получить значение, переведенное в квадратные метры.
Как перевести ареи в квадратные метры
Чтобы преобразовать единицу измерения в квадратный метр, умножьте площадь на коэффициент преобразования.
Поскольку одна равна 100 квадратных метров, вы можете использовать эту простую формулу для преобразования:
квадратные метры = ар × 100
Площадь в квадратных метрах равна арам, умноженным на 100.
Например, вот как преобразовать 5 ар в квадратные метры, используя формулу выше.5 a = (5 × 100) = 500 кв.м
Сколько квадратных метров в доме?
Площадь соток составляет 100 квадратных метров, поэтому мы используем это значение в приведенной выше формуле.
1 а = 100 кв м
Ареи и квадратные метры — единицы измерения площади. Продолжайте читать, чтобы узнать больше о каждой единице измерения.
Один равен 100 квадратных метрам, или площади квадрата со сторонами 10 метров.
Ар — это метрическая единица измерения площади вне системы СИ. Сокращенное обозначение Ares — a ; например, 1 ар можно записать как 1 а.
Один квадратный метр равен площади квадрата со стороной 1 метр.
[1]
Квадратный метр или квадратный метр — производная единица измерения площади в системе СИ в метрической системе. Квадратный метр иногда также называют квадратным м. Квадратные метры могут быть сокращены до кв. М , а иногда также сокращаются до м² .Например, 1 квадратный метр можно записать как 1 кв. М или 1 м².
Воспользуйтесь нашим калькулятором квадратных метров, чтобы рассчитать площадь помещения.
Как рассчитать квадратные метры комнаты
Обновлено 3 ноября 2020 г.
Лиза Мэлони
Если вы когда-либо пытались выложить пол, расставить мебель или спорили о том, кому достанется большая спальня, вы уже понимать важность знания размера комнаты.В США большинство напольных покрытий, мебели и других материалов измеряются в футах, поэтому имеет смысл рассчитывать размер комнаты в квадратных футах. Однако, если вы смотрите на мебель или материалы для пола — или на потенциального соседа по комнате из любой точки мира — вам нужно вместо этого рассчитать размер комнаты в квадратных метрах.
TL; DR (слишком долго; не читал)
Чтобы вычислить площадь прямоугольной комнаты в квадратных метрах, умножьте ее длину в метрах на ширину в метрах.Если комната необычной формы, разбейте ее на отдельные прямоугольники, вычислите площадь в квадратных метрах для каждого прямоугольника, а затем сложите площади всех прямоугольников для общей площади комнаты в квадратных метрах.
Измерьте длину и ширину
Чтобы рассчитать площадь комнаты, вам необходимо знать ее длину и ширину. Поскольку вы хотите получить результат в квадратных метрах, оба измерения следует проводить в метрах. У большинства измерительных лент есть метрические измерения на одной стороне, поэтому просто убедитесь, что вы читаете правую сторону ленты, и всегда записывайте измерения, чтобы сократить ошибки и избежать необходимости повторного измерения, если вы забудете.
Преобразование метров в футы
Если вы уже измерили комнату в футах, повторять измерения не нужно.
2
Когда вы умножаете одно измерение в метрах на другое измерение в метрах, результат всегда должен быть помечен как квадратные метры, чтобы избежать путаницы.Вы также можете записать квадратные метры как метры 2 или m 2 , что читается как квадратные метры.
Измерение комнат нечетной формы
Формула работает, если ваша комната имеет квадратную или прямоугольную форму, но иногда комнаты имеют L-образную форму, или, может быть, вы хотите измерить свободное пространство на полу вокруг мебели, которая уже находится в комнате. В этом случае проще всего разбить форму комнаты на отдельные прямоугольники. Вычислите площадь каждого прямоугольника в квадратных метрах, а затем сложите площади, чтобы получить общую площадь комнаты в квадратных метрах.2
Расчет площади в квадратных метрах
Измерение
Выберите метр или метрическую рулетку. Выберите линейку-линейку или рулетку с напечатанными на ней метрами (м) или сантиметрами (см).Эти инструменты упростят расчет квадратных метров, поскольку они были разработаны в одной системе измерения.
Измерьте длину измеряемой области. Квадратные метры — это единица измерения площади или размера двухмерного объекта, такого как пол или поле.Используйте свой измерительный инструмент, чтобы измерить одну сторону объекта от одного угла до другого. Запишите результат.
Если объект длиннее 1 метра, не забудьте включить в измерение и метровую, и сантиметровую части. Например, «2 метра 35 сантиметров».
Если вы не можете измерить всю длину сразу, делайте это поэтапно. Разложите измерительный инструмент, затем положите камень или другой небольшой предмет точно на легко запоминающейся отметке (например, 1 метр или 25 сантиметров).Возьмите инструмент и снова положите его, начиная с небольшого предмета. Повторяйте, пока не будет покрыта вся длина, и сложите все свои измерения вместе.
Измерьте ширину. Используйте тот же инструмент, чтобы измерить ширину той же области или объекта.
Сторона, которую вы измеряете на этом этапе, должна быть расположена под углом около 90 ° к длине объекта, который вы измерили ранее, как две стороны квадрата, расположенные рядом друг с другом. Запишите и этот номер.
Расчеты
Если измеряемый объект не намного меньше 1 метра, при измерениях можно округлить до ближайшего сантиметра.Например, если ширина немного превышает отметку в 1 метр 8 сантиметров, просто используйте в качестве измерения «1 м 8 см» без использования десятичных знаков или миллиметров.Преобразование из сантиметров в метры. Обычно измерения не делятся равномерно на метры. Вместо этого у вас будут измерения в метрах и сантиметрах, например «2 метра 35 сантиметров». Поскольку 1 сантиметр = 0,01 метра, вы можете преобразовать сантиметр в метры, переместив десятичную запятую на две цифры влево.
Вот пара примеров:
35 см = 0,35 м, поэтому 2 м 35 см = 2 м + 0,35 м = 2,35 м
8 см = 0,08 м, поэтому 1 м 8 см = 1,08 мУмножьте длину и ширину.
После того, как оба измерения будут преобразованы в метры, умножьте их вместе, чтобы получить измерение площади в квадратных метрах. При необходимости воспользуйтесь калькулятором. Например:
2,35 м x 1,08 м = 2,538 квадратных метра (м2).Округлите до более удобного размера. Если в качестве ответа вы получите длинную десятичную дробь, например, 2.538 квадратных метров, вы, вероятно, захотите округлить до числа с меньшим количеством цифр, например 2,54 квадратных метра. Фактически, поскольку вы, возможно, неправильно измерили до мельчайших долей метра, последние цифры, вероятно, в любом случае неточны. В большинстве случаев вы можете округлить до ближайшего сантиметра (0,01 м).
Всякий раз, когда вы умножаете два числа на одинаковые единицы (например, метры), ответ всегда будет в форме квадрата этой единицы (м2 или квадратные метры).
Заказ
Вы можете умножить квадратный метр на три, чтобы определить, сколько рулонов травы вам понадобится.


 м. Можно спросить – это сколько? Если после запятой вставить 28 нолей, и только потом единицу, получится наглядный ответ.
м. Можно спросить – это сколько? Если после запятой вставить 28 нолей, и только потом единицу, получится наглядный ответ.

 Снова округлим до 0,67 м².
Снова округлим до 0,67 м².
 м.
м. м.
м. Округляя получаем 9,0 м2.
Округляя получаем 9,0 м2.
 Получив значение фигур, цифры складывают;
Получив значение фигур, цифры складывают;
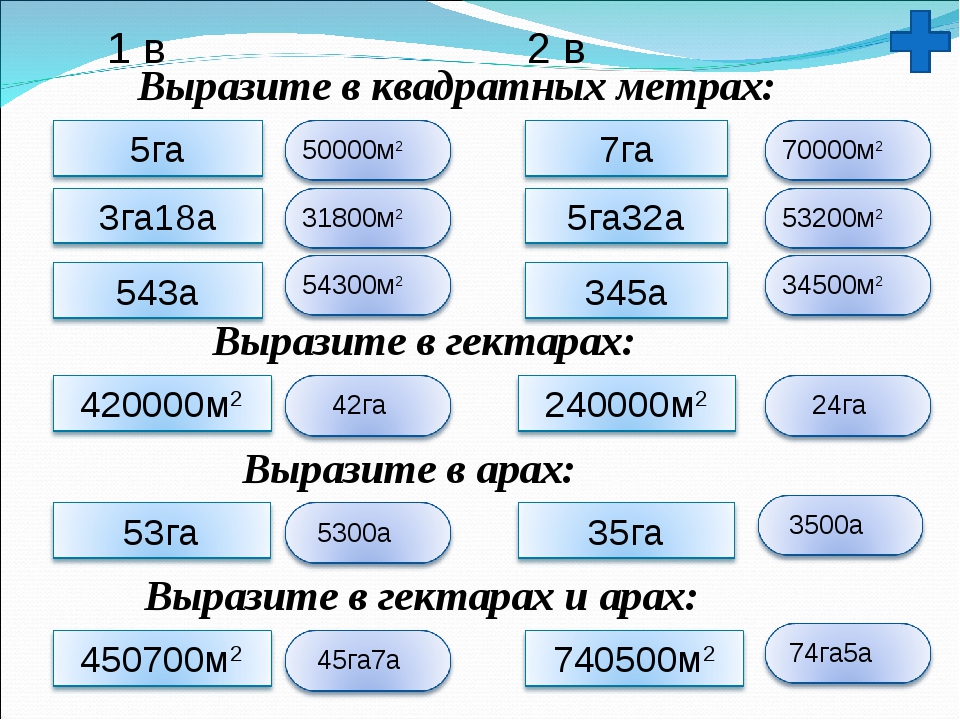
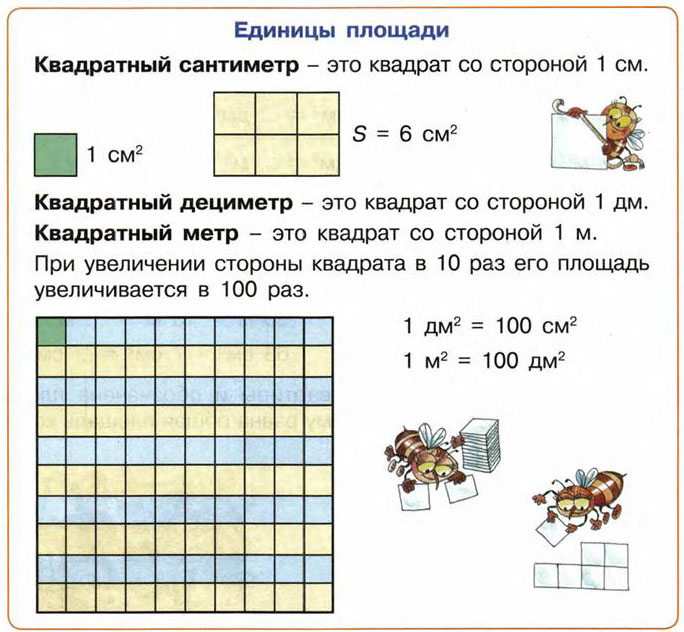
 Следует отметить, что не нужно путать вычисление площади участка с его периметром. Вычисляя периметр, можно найти общую длину сторон, а не площадь.
Следует отметить, что не нужно путать вычисление площади участка с его периметром. Вычисляя периметр, можно найти общую длину сторон, а не площадь.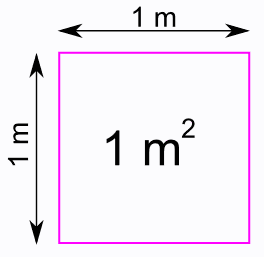 Это максимально достоверный способ узнать размеры участка: неправильная форма будет разбита на несколько равных треугольников, подсчитана их площадь по отдельности и в сумме. Результат – точное количество соток, включая самые неудобные для «ручных» замеров места.
Это максимально достоверный способ узнать размеры участка: неправильная форма будет разбита на несколько равных треугольников, подсчитана их площадь по отдельности и в сумме. Результат – точное количество соток, включая самые неудобные для «ручных» замеров места.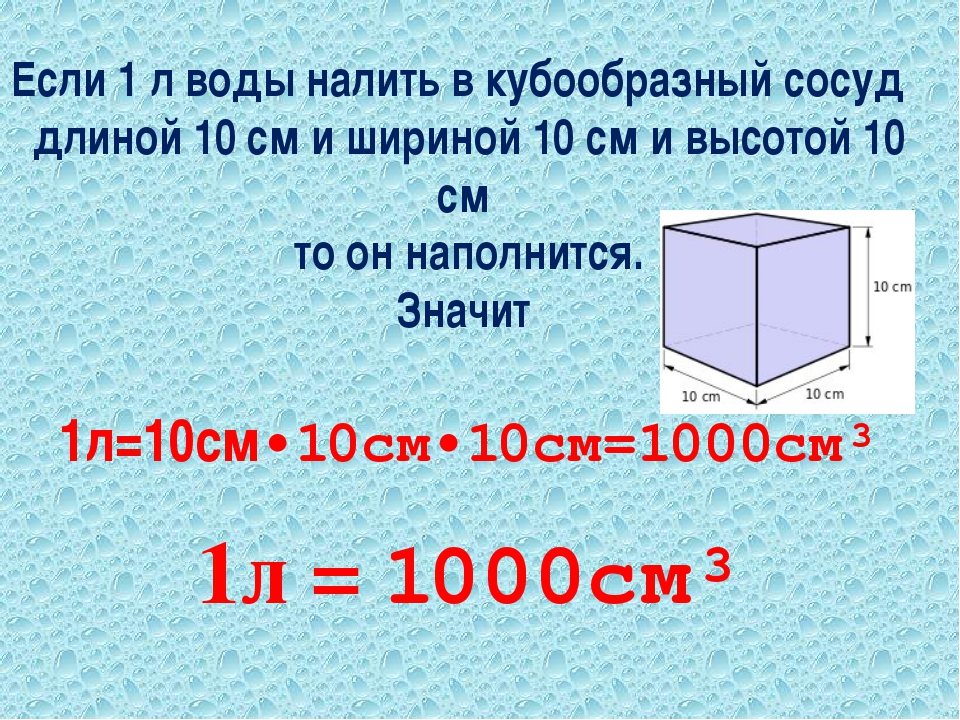
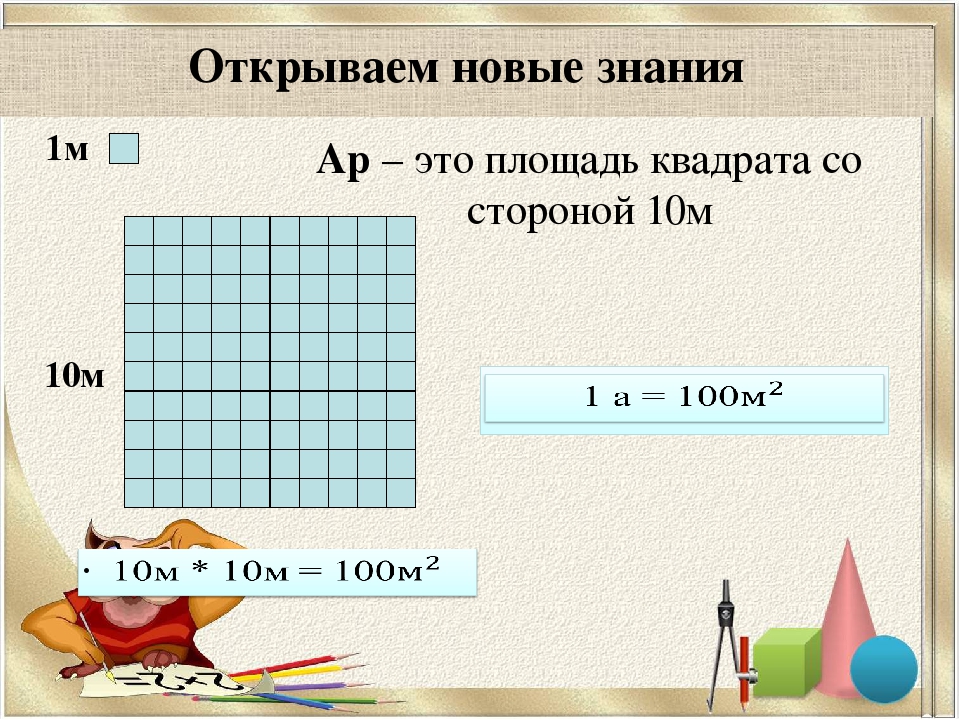 Поскольку вы можете умножить что угодно на 1 и при этом сохранить исходное значение, но в других единицах, настройте его так, чтобы ft компенсировались, оставив вас с m.
Поскольку вы можете умножить что угодно на 1 и при этом сохранить исходное значение, но в других единицах, настройте его так, чтобы ft компенсировались, оставив вас с m. Разделив обе части уравнения на 0,092
Разделив обе части уравнения на 0,092 Двор
Двор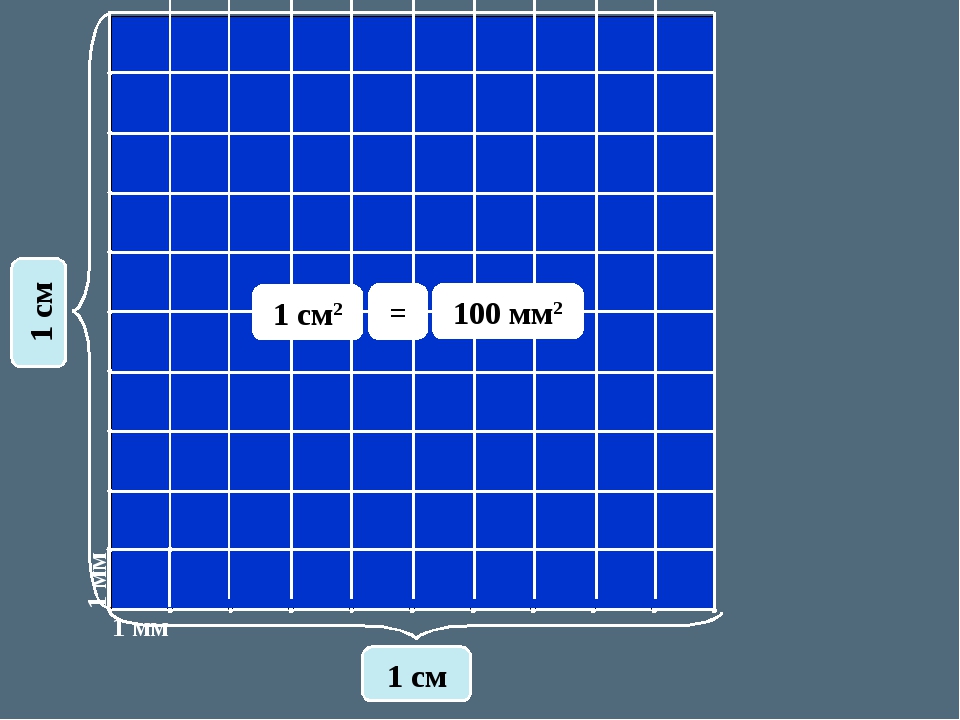 000001
000001 , Дэниел (главный редактор). CRC Handbook of Chemistry and Physics, 89th Edition New York, NY: CRC Press, p. 1-28, 2008.
, Дэниел (главный редактор). CRC Handbook of Chemistry and Physics, 89th Edition New York, NY: CRC Press, p. 1-28, 2008.
 [1]
[1] 
 2
2 Эти инструменты упростят расчет квадратных метров, поскольку они были разработаны в одной системе измерения.
Эти инструменты упростят расчет квадратных метров, поскольку они были разработаны в одной системе измерения. Сторона, которую вы измеряете на этом этапе, должна быть расположена под углом около 90 ° к длине объекта, который вы измерили ранее, как две стороны квадрата, расположенные рядом друг с другом. Запишите и этот номер.
Сторона, которую вы измеряете на этом этапе, должна быть расположена под углом около 90 ° к длине объекта, который вы измерили ранее, как две стороны квадрата, расположенные рядом друг с другом. Запишите и этот номер. После того, как оба измерения будут преобразованы в метры, умножьте их вместе, чтобы получить измерение площади в квадратных метрах. При необходимости воспользуйтесь калькулятором. Например:
После того, как оба измерения будут преобразованы в метры, умножьте их вместе, чтобы получить измерение площади в квадратных метрах. При необходимости воспользуйтесь калькулятором. Например: