Единицы силы. Динамометр. Видеоурок. Физика 7 Класс

Тема: Взаимодействие тел

Урок: Единицы силы. Динамометр

Прежде всего, вспомним, что такое сила. Когда на тело действует другое тело, физики говорят, что со стороны другого тела на данное тело действует сила.

Сила – это физическая величина, характеризующая действие одного тела на другое.

Сила обозначается латинской буквой F, а единица силы в честь английского физика Исаака Ньютона называется ньютоном (пишем с маленькой буквы!) и обозначается Н (пишем заглавную букву, так как единица названа в честь ученого). Итак,

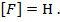
Наравне с ньютоном, используются кратные и дольные единицы силы:

килоньютон 1 кН = 1000 Н;

меганьютон 1 МН = 1000000 Н;

миллиньютон 1 мН = 0,001 Н;

микроньютон 1 мкН = 0,000001 Н и т. д.

Под действием силы скорость тела изменяется. Другими словами, тело начинает двигаться не равномерно, а ускоренно. Точнее, равноускоренно: за равные промежутки времени скорость тела меняется одинаково. Именно изменение скорости тела под действием силы физики используют для определения единицы силы в 1 Н.

Единицы измерения новых физических величин выражают через так называемые основные единицы – единицы массы, длины, времени. В системе СИ – это килограмм, метр и секунда.

Пусть под действием некоторой силы скорость тела массой 1 кг изменяет свою скорость на 1 м/с за каждую секунду. Именно такая сила и принимается за 1 ньютон

.

Один ньютон (1 Н) – это сила, под действием которой тело массой 1 кг изменяет свою скорость на 1 м/с каждую секунду.

Экспериментально установлено, что сила тяжести, действующая вблизи поверхности Земли на тело массой 102 г, равна 1 Н. Масса 102 г составляет приблизительно 1/10 кг, или, если быть более точным,

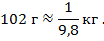
Но это означает, что на тело массой 1 кг, то есть на тело в 9,8 раз большей массы, у поверхности Земли будет действовать сила тяжести 9,8 Н. Таким образом, чтобы найти силу тяжести, действующую на тело любой массы, нужно значение массы (в кг) умножить на коэффициент, который принято обозначать буквой

g:

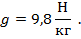
Мы видим, что этот коэффициент численно равен силе тяжести, которая действует на тело массой 1 кг. Он носит название ускорение свободного падения. Происхождение названия тесно связано с определением силы в 1 ньютон. Ведь если на тело массой 1 кг действует сила не 1 Н, а 9,8 Н, то под действием этой силы тело будет изменять свою скорость (ускоряться) не на 1 м/с, а на 9,8 м/с каждую секунду. В старшей школе этот вопрос будет рассмотрен более подробно.

Теперь можно записать формулу, позволяющую рассчитать силу тяжести, действующую на тело произвольной массы m(Рис. 1).

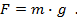
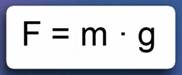
Рис. 1. Формула для расчета силы тяжести

Следует знать, что ускорение свободного падения равно 9,8 Н/кг только у поверхности Земли и с высотой уменьшается. Например, на высоте 6400 км над Землей оно меньше в 4 раза. Однако при решении задач этой зависимостью мы будем пренебрегать. Кроме того, на Луне и других небесных телах также действует сила тяжести, и на каждом небесном теле ускорение свободного падения имеет свое значение.

На практике часто приходится измерять силу. Для этого используется устройство, которое называется динамометр. Основой динамометра является пружина, к которой прикладывают измеряемую силу. Каждый динамометр, помимо пружины, имеет шкалу, на которую нанесены значения силы. Один из концов пружины снабжен стрелкой, которая указывает на шкале, какая сила приложена к динамометру (Рис. 2).

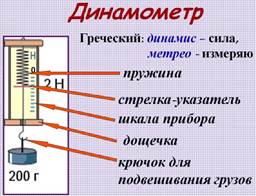
Рис. 2. Устройство динамометра

В зависимости от упругих свойств пружины, использованной в динамометре (от ее жесткости), под действием одной и той же силы пружина может удлиняться больше или меньше. Это позволяет изготавливать динамометры с различными пределами измерения (Рис. 3).

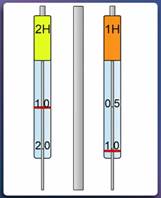
Рис. 3. Динамометры с пределами измерения 2 Н и 1 Н

Существуют динамометры с пределом измерения в несколько килоньютонов и больше. В них используется пружина с очень большой жесткостью (Рис. 4).

Рис. 4. Динамометр с пределом измерения 2 кН

Если подвесить к динамометру груз, то по показаниям динамометра можно определить массу груза. Например, если динамометр с подвешенным к нему грузом показывает силу 1 Н, значит, масса груза равна 102 г.

Обратим внимание на то, что сила имеет не только численное значение, но и направление. Такие величины называют векторными. Например, скорость – это векторная величина. Сила – также векторная величина (говорят еще, что сила – вектор).

Рассмотрим следующий пример:

Тело массой 2 кг подвешено на пружине. Необходимо изобразить силу тяжести, с которой Земля притягивает это тело, и вес тела.

Вспомним, что сила тяжести действует на тело, а вес – это сила, с которой тело действует на подвес. Если подвес неподвижен, то численное значение и направление веса такие же, как у силы тяжести. Вес, как и сила тяжести, рассчитываются по формуле, изображенной на рис. 1. Массу 2 кг необходимо умножить на ускорение свободного падения 9,8 Н/кг. При не слишком точных расчетах часто ускорение свободного падения принимают равным 10 Н/кг. Тогда сила тяжести и вес приблизительно будут равны 20 Н.

Для изображения векторов силы тяжести и веса на рисунке необходимо выбрать и показать на рисунке масштаб в виде отрезка, соответствующего определенному значению силы (например, 10 Н).

Тело на рисунке изобразим в виде шара. Точка приложения силы тяжести – центр этого шара. Силу изобразим в виде стрелки, начало которой расположено в точке приложения силы. Стрелку направим вертикально вниз, так как сила тяжести направлена к центру Земли. Длина стрелки, в соответствии с выбранным масштабом, равна двум отрезкам. Рядом со стрелкой изображаем букву 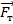, которой обозначается сила тяжести. Так как на чертеже мы указали направление силы, то над буквой ставится маленькая стрелка, чтобы подчеркнуть, что мы изображаем векторную

величину.

Поскольку вес тела приложен к подвесу, начало стрелки, изображающей вес, помещаем в нижней части подвеса. При изображении также соблюдаем масштаб. Рядом помещаем букву 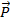, обозначающую вес, не забывая над буквой поместить небольшую стрелку.

Полное решение задачи будет выглядеть так (Рис. 5).

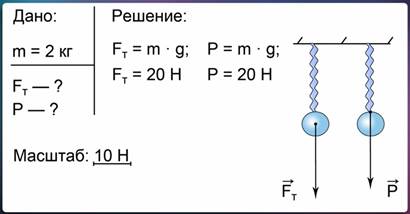
Рис. 5. Оформленное решение задачи

Еще раз обратите внимание на то, что в рассмотренной выше задаче численные значения и направления силы тяжести и веса оказались одинаковыми, а точки приложения – различными.

При расчете и изображении любой силы необходимо учитывать три фактора:

· численное значение (модуль) силы;

· направление силы;

· точку приложения силы.

Сила – физическая величина, описывающая действие одного тела на другое. Обычно она обозначается буквой F. Единица измерения силы – ньютон. Для того чтобы рассчитать значение силы тяжести, необходимо знать ускорение свободного падения, которое у поверхности Земли составляет 9,8 Н/кг. С такой силой Земля притягивает к себе тело массой 1 кг. При изображении силы необходимо учитывать ее числовое значение, направление и точку приложения.

 

Список литературы

1. Перышкин А. В. Физика. 7 кл. – 14-е изд., стереотип. – М.: Дрофа, 2010.
2. Перышкин А. В. Сборник задач по физике, 7–9 кл.: 5-е изд., стереотип. – М: Издательство «Экзамен», 2010.
3. Лукашик В. И., Иванова Е. В. Сборник задач по физике для 7–9 классов общеобразовательных учреждений. – 17-е изд. – М.: Просвещение, 2004.

 

Дополнительные ссылки на ресурсы сети Интернет

1. Единая коллекция цифровых образовательных ресурсов (Источник).
2. Единая коллекция цифровых образовательных ресурсов (Источник).
3. Единая коллекция цифровых образовательных ресурсов (Источник).
4. Единая коллекция цифровых образовательных ресурсов (Источник).

 

Домашнее задание

1. Лукашик В. И., Иванова Е. В. Сборник задач по физике для 7–9 классов №327, 335–338, 351.

Сила — Википедия

Си́ла — физическая векторная величина, являющаяся мерой воздействия на данное тело со стороны других тел или полей. Приложение силы обусловливает изменение скорости тела или появление деформаций и механических напряжений. Деформация может возникать как в самом теле, так и в фиксирующих его объектах — например, пружинах.

Воздействие всегда осуществляется посредством полей, создаваемых телами и воспринимаемых рассматриваемым телом. Различные взаимодействия сводятся к четырём фундаментальным; согласно Стандартной модели физики элементарных частиц, эти фундаментальные взаимодействия (слабое, электромагнитное, сильное и, возможно, гравитационное) реализуются путём обмена калибровочными бозонами^[1].

Для обозначения силы обычно используется символ F — от лат. fortis (сильный).

Важнейший физический закон, в который входит сила, — второй закон Ньютона. Он гласит, что в инерциальных системах отсчёта ускорение материальной точки по направлению совпадает с приложенной силой, а по модулю пропорционально модулю силы и обратно пропорционально массе материальной точки.

Слово «сила» в русском языке является многозначным и нередко используется (само или в сочетаниях, в науке и обиходных ситуациях) в смыслах, отличных от физического определения термина.

Характеристики силы[править | править код]

Сила является векторной величиной. Она характеризуется модулем, направлением и точкой приложения. Также используют понятие линия действия силы, означающее проходящую через точку приложения силы прямую, вдоль которой направлена сила.

Зависимость силы от расстояния между телами может иметь различный вид, однако, как правило, при больших расстояниях сила стремится к нулю — поэтому отдалением рассматриваемого тела от других тел с хорошей точностью обеспечивается ситуация «отсутствия внешних сил»^[2]. Исключения возможны в некоторых задачах космологии, касающихся тёмной энергии^[3].

Кроме разделения по типу фундаментальных взаимодействий, существуют иные классификации сил, в том числе: внешние—внутренние (то есть действующие на материальные точки (тела) данной механической системы со стороны материальных точек (тел) не принадлежащих этой системе и силы взаимодействия между материальными точками (телами) данной системы^[4]), потенциальные и нет (потенциально ли поле изучаемых сил), упругие—диссипативные, сосредоточенные—распределённые (приложены в одной или многих точках), постоянные или переменные во времени.

При переходе из одной инерциальной системы отсчёта в другую преобразование сил осуществляется так же, как и полей соответствующей природы (например, электромагнитных, если сила электромагнитная). В пределе малых скоростей можно считать силу инвариантом.

Системой сил называется совокупность сил, действующих на рассматриваемое тело или на точки механической системы. Две системы сил называют эквивалентными, если их действие по отдельности на одно и то же твердое тело или материальную точку одинаково при прочих равных условиях^[4].

Уравновешенной системой сил (или системой сил, эквивалентной нулю) называется система сил, действие которой на твердое тело или материальную точку не приводит к изменению их кинематического состояния^[4].

Размерность силы[править | править код]

Размерность силы в Международной системе величин (англ. International System of Quantities, ISQ), на которой базируется Международная система единиц (СИ), и в системе величин LMT, используемой в качестве основы для системы единиц СГС, — LMT⁻². Единицей измерения в СИ является ньютон (русское обозначение: Н; международное: N), в системе СГС — дина (русское обозначение: дин, международное: dyn).

Равнодействующая системы сил[править | править код]

Если к не закреплённому телу приложено несколько сил, то каждая из них сообщает телу такое ускорение, какое она сообщила бы в отсутствие действия других сил. Это утверждение, основанное на опытных фактах, носит название принципа независимости действия сил (принципа суперпозиции). Поэтому при расчёте ускорения тела все действующие на него силы заменяют одной силой, называемой равнодействующей, а именно геометрической суммой всех действующих сил. В частном случае равенства равнодействующей сил нулю ускорение тела также будет нулевым. На этом основано измерение величины исследуемой силы, когда она компенсируется силой, величина которой известна.

Измерение сил[править | править код]

Для измерения сил используются два метода: статический и динамический^[5].

• Статический метод заключается в уравновешивании измеряемой силы другой силой, значение которой известно. Например, в качестве уравновешивающей силы может выступать сила упругости, возникающая в градуированной пружине, деформированной исследуемой силой. На использовании статического метода основаны приборы, называемые динамометрами.
• Динамический метод основан на использовании уравнения второго закона Ньютона ma→=F→{\displaystyle m{\vec {a}}={\vec {F}}}. Уравнение позволяет найти силу F→{\displaystyle {\vec {F}}}, действующую на тело, если известны масса тела m{\displaystyle m} и ускорение a→{\displaystyle {\vec {a}}} его поступательного движения относительно инерциальной системы отсчёта.

В древнем мире[править | править код]

Человечество вначале стало воспринимать понятие силы через непосредственный опыт передвижения тяжёлых предметов. «Сила», «мощность», «работа» при этом были синонимами (как и в современном языке за пределами естествознания). Перенос личных ощущений на объекты природы привёл к антропоморфизму: все предметы, которые могут воздействовать на другие (реки, камни, деревья) должны быть живыми, в живых существах должна содержаться та же сила, которую человек чувствовал в себе.

С развитием цивилизации сила была обожествлена, причём как египетский, так и месопотамский боги силы символизировали не только жестокость и мощь, но и наведение порядка во вселенной^[6]. Всемогущий Бог Библии также несёт в своих именах и эпитетах ассоциации с силой^[7].

В античности[править | править код]

Когда греческие учёные стали задумываться о природе движения, понятие силы возникло как часть учения Гераклита о статике как балансе противоположностей^[8]. Эмпедокл и Анаксагор пытались объяснить причину движения и пришли к понятиям, близким к понятию силы^[8]. У Анаксагора «ум» движет внешней по отношению к нему материей^[9]. У Эмпедокла движение вызывается борьбой двух начал, «любви» (филии) и «вражды» (фобии)^[9], которые Платон рассматривал как притяжение и отталкивание^[10]. При этом взаимодействие, по Платону, объяснялось в терминах четырёх элементов (огня, воды, земли и воздуха): близкие вещи притягиваются, земля к земле, вода к воде, огонь к огню^[11]. В древнегреческой науке каждый элемент также имел своё место в природе, которое старался занять. Таким образом, сила тяжести, например, объяснялась двумя способами: притяжением подобных вещей и стремлением элементов занять своё место^[12]. В отличие от Платона, Аристотель последовательно занимал вторую позицию, что отложило концепцию общей силы тяготения, которая бы объясняла движение земных и небесных тел, до времён Ньютона^[12].

Для обозначения понятия силы Платон использовал термин «динамис» («возможность» движения). Термин употреблялся в расширенном смысле, близком к современному понятию мощности: химические реакции, тепло и свет все также представляли собой динамисы^[13].

Аристотель рассматривал две разные силы: присущую самому телу («природу», физис) и силу, с которой одно тело тянет или толкает другое (при этом тела должны быть в контакте)^[14]. Именно это понятие о силе и легло в основу аристотелевой механики, хотя дуализм и препятствовал количественному определению силы взаимодействия двух тел (так как вес был природной силой, не связанной с взаимодействием, и потому не мог использоваться в качестве стандарта)^[15]. В случае природного движения (падения тяжёлого или подъёма лёгкого тела) Аристотель предложил формулу для скорости в виде отношения плотностей движущегося тела A и среды, сквозь которую происходит движение, B: v=A/B^[16] (очевидная проблема для случая равных плотностей была отмечена уже в VI веке^[17]).

Изучением сил в процессе конструирования простых механизмов занимался в III в. до н. э. Архимед^[18]. Архимед рассматривал силы в статике и чисто геометрически, и потому его вклад в развитие понятия силы незначителен^[19].

Вклад в развитие понятие силы внесли стоики. Согласно их учению, силы неразрывно связывали два тела через дальнодействующую «симпатию» или (у Посидония) через всеобщее напряжение, пронизывающее всё пространство. Стоики пришли к этим выводам путём наблюдения за приливами, где взаимодействие Луны, Солнца и воды в океане было трудно объяснить с позиции Аристотелева близкодействия (сам Аристотель считал, что Солнце, садясь в океан, вызывает ветры, приводящие к приливам)^[20].

В доклассической механике[править | править код]

Бэкон и Оккам вернули в науку идею о дальнодействии.

Бэкон называл дальнодействующие силы species (обычно этот специфичный для Бэкона термин не переводится) и рассматривал их распространение в среде как цепочку близких взаимодействий. Такие силы, по Бэкону, имели вполне телесный характер, ближайшим эквивалентом в современной физике является волна^[21].

Оккам первым отказался от аристотелевского описания взаимодействия как непосредственного контакта и декларировал возможность движителя воздействовать на движимое на расстоянии, приведя в качестве одного из примеров магниты^[22].

Ревизии подвергалась и аристотелевская формула v=A/B. Уже в VI веке Иоанн Филопон рассматривал в качестве правой части разность A-B, что кроме проблемной ситуации с одинаковыми плотностями позволило также описать движение в вакууме^[23]. В XIV веке Брадвардин предложил формулу v=log(A/B)^[24].

У Кеплера[править | править код]

Взгляды Кеплера на силу претерпели быстрое изменение. Ещё в 1600 году Кеплер рассматривает силы как свойство, подобное душе, которое руководит движением небесных тел. Однако уже к 1605 году Кеплер пришёл к выводу, что притяжение — это не действие, а реакция, силы притяжения относятся к материальному миру и подлежат математическому изучению. В 1607 году Кеплер пришёл к выводу, что приливы вызываются воздействием силы притяжения Луны на океаны^[25]. По мнению М. Дженнера, Кеплер пришёл к идее единой теории тяготения, охватывающей как падение тел, так и движение Луны, до Ньютона^[26].

В классической механике[править | править код]

С зарождением классической механики Бекманом и Декартом был сформулирован закон сохранения количества движения. После осознания этого факта, который похоронил аристотелевскую связь силы и скорости, у исследователей оставалось два выхода: определить силу как причину изменения скорости или отбросить понятие силы как таковое. Сам Декарт вначале применял понятие силы, чтобы объяснить ускоренное падение тела на землю, но со временем в попытке геометризации физики пришёл к выводу, что понятие силы является искусственным, и в 1629 году описывал процесс свободного падения без упоминания «силы»^[27]. С другой стороны, Галилей недвусмысленно рассматривал силу как причину увеличения скорости свободного падения^[28].

У Ньютона[править | править код]

В трудах Ньютона понятие силы было тесно связано с тяготением, поскольку интерпретация кеплеровских результатов в области движения планет в то время занимала все умы^[29]. Впервые понятие силы (лат. vis) встречается у Ньютона в «Началах» в двух контекстах: «присущей силы» (лат. vis insita), ньютоновской силы инерции и «приложенной силы» (лат. vis impressa), отвечающей за изменение движения тела. Ньютон также отдельно выделял центростремительную силу (к которой относил тяготение) с несколькими разновидностями: абсолютную силу (подобную современному полю тяготения), ускоряющую силу (эффект тяготения на единицу массы, современное ускорение) и движущую (произведение массы на ускорение)^[30]. Ньютон не даёт общего определения силы. Как отмечает М. Дженнер, второй закон Ньютона не является определением силы у самого автора закона (который явно различал определения и законы), сила у Ньютона является пресуществующим понятием, интуитивно эквивалентным силе мускулов^[31].

Современность[править | править код]

Конец XX века охарактеризовался спорами о том, необходимо ли в науке понятие силы и существуют ли силы в принципе — или это только термин, введённый для удобства^[32].

Бигелоу с соавторами в 1988 году аргументировали, что силы по сути определяют причинно-следственные отношения и потому не могут быть отброшены^[33]. М. Джеммер на это возразил, что в Стандартной модели и других физических теориях сила трактуется лишь как обмен моментом импульса, понятие силы потому сводится к более простому «взаимодействию» между частицами. Это взаимодействие описывается в терминах обмена дополнительными частицами (фотонами, глюонами, бозонами и, возможно, гравитонами)^[32]. Джеммер приводит следующее упрощённое пояснение: два конькобежца скользят по льду плечо к плечу, у обоих в руках находится по мячу. Быстрый и одновременный обмен мячами приведёт к отталкивающему взаимодействию^[34].

Стиннер отмечает, что эйнштейновский принцип эквивалентности сил гравитации и инерции по сути уничтожает понятие силы, в общей теории относительности внешние силы (F из уравнения F=ma) отсутствуют^[35].

Ньютон задался целью описать движение объектов, используя понятия инерции и силы. Сделав это, он попутно установил, что всякое механическое движение подчиняется общим законам сохранения. В 1687 г. Ньютон опубликовал свой знаменитый труд «Математические начала натуральной философии», в котором изложил три основополагающих закона классической механики (законы Ньютона)^[36][37].

Первый закон Ньютона[править | править код]

Первый закон Ньютона утверждает, что существуют системы отсчёта, в которых тела сохраняют состояние покоя или равномерного прямолинейного движения при отсутствии действий на них со стороны других тел или при взаимной компенсации этих воздействий^[37]. Такие системы отсчёта называются инерциальными. Ньютон предположил, что каждый массивный (подразумевается: «обладающий массой», а не «громоздкий») объект имеет определённый запас инерции, характеризующий «естественное состояние» движения этого объекта. Эта идея отрицает взгляд Аристотеля, который рассматривал только покой «естественным состоянием» объекта. Первый закон Ньютона противоречит аристотелевской физике, одним из положений которой является утверждение о том, что тело может двигаться с постоянной скоростью лишь под действием силы. Тот факт, что в механике Ньютона в инерциальных системах отсчёта покой неотличим от равномерного прямолинейного движения, является обоснованием принципа относительности Галилея. Среди совокупности тел принципиально невозможно определить, какие из них находятся «в движении», а какие «покоятся». Говорить о движении можно лишь относительно конкретной системы отсчёта. Законы механики выполняются одинаково во всех инерциальных системах, другими словами, все они механически эквивалентны. Последнее следует из так называемых преобразований Галилея^[38].

Второй закон Ньютона[править | править код]

Второй закон Ньютона имеет вид:

ma→=F→.{\displaystyle m{\vec {a}}={\vec {F}}.}

где m{\displaystyle m} — масса материальной точки, a→{\displaystyle {\vec {a}}} − её ускорение, F→{\displaystyle {\vec {F}}} — равнодействующая приложенных сил. Считается, что это «вторая самая известная формула в физике», хотя сам Ньютон никогда явным образом не записывал свой второй закон в этом виде. Впервые данную форму закона можно встретить в трудах К. Маклорена и Л. Эйлера.

Поскольку в любой инерциальной системе отсчёта ускорение тела одинаково и не меняется при переходе от одной системы к другой, сила тоже инвариантна по отношению к такому переходу.

Во всех явлениях природы сила, независимо от своего происхождения, проявляется только в механическом смысле, то есть как причина нарушения равномерного и прямолинейного движения тела в инерциальной системе координат. Обратная ситуация, а именно установление факта такого движения, свидетельствует не об отсутствии действующих на тело сил, а лишь о том, что действия этих сил взаимно уравновешиваются. Иначе: их векторная сумма есть вектор с модулем, равным нулю.

Второй закон Ньютона не играет роль определения силы, но позволяет находить её величину. Например, знание массы планеты и её центростремительного ускорения при движении по орбите позволяет вычислить величину силы гравитационного притяжения, действующей на эту планету со стороны Солнца.

Третий закон Ньютона[править | править код]

Для любых двух тел (назовём их тело 1 и тело 2) третий закон Ньютона утверждает, что сила действия тела 1 на тело 2 сопровождается появлением равной по модулю, но противоположной по направлению силы, действующей на тело 1 со стороны тела 2^[39]. Математически закон записывается так:

F→1,2=−F→2,1.{\displaystyle {\vec {F}}_{1,2}=-{\vec {F}}_{2,1}.}

Этот закон означает, что силы всегда возникают парами «действие-противодействие»^[37]. Если тело 1 и тело 2 находятся в одной системе, то суммарная сила в системе, обусловленная взаимодействием этих тел, равна нулю:

F→1,2+F→2,1=0.{\displaystyle {\vec {F}}_{1,2}+{\vec {F}}_{\mathrm {2,1} }=0.}

Это означает, что в замкнутой системе не существует несбалансированных внутренних сил. Это приводит к тому, что центр масс замкнутой системы (то есть такой, на которую не действуют внешние силы) не может двигаться с ускорением. Отдельные части системы могут ускоряться, но лишь таким образом, что система в целом остаётся в состоянии покоя или равномерного прямолинейного движения. Однако, в случае, если внешние силы подействуют на систему, её центр масс начнёт двигаться с ускорением, пропорциональным внешней результирующей силе и обратно пропорциональным массе системы^[1].

Кроме того, так как силы взаимодействия всегда направлены вдоль прямой, соединяющей взаимодействующие точки, равен нулю и суммарный момент этих сил (относительно любой точки):

(r→1−r→0)×F→1,2+(r→2−r→0)×F→2,1=(r→1−r→2)×F→1,2=0{\displaystyle ({\vec {r}}_{1}-{\vec {r}}_{0})\times {\vec {F}}_{1,2}+({\vec {r}}_{2}-{\vec {r}}_{0})\times {\vec {F}}_{\mathrm {2,1} }=({\vec {r}}_{1}-{\vec {r}}_{2})\times {\vec {F}}_{1,2}=0}

Все силы в природе основаны на четырёх типах фундаментальных взаимодействий. Максимальная скорость распространения всех видов взаимодействия равна скорости света в вакууме. Электромагнитные силы действуют между электрически заряженными телами, гравитационные — между массивными объектами. Сильное и слабое проявляются только на очень малых расстояниях, они ответственны за возникновение взаимодействия между субатомными частицами, включая нуклоны, из которых состоят атомные ядра.

Интенсивность сильного и слабого взаимодействия измеряется в единицах энергии (электрон-вольтах), а не единицах силы, и потому применение к ним термина «сила» объясняется существующей с античности традицией объяснять любые явления в окружаемом мире действием специфических для каждого явления «сил».

Понятие силы не может быть применено по отношению к явлениям субатомного мира. Это понятие из арсенала классической физики, ассоциирующейся (пусть даже только подсознательно) с ньютоновскими представлениями о силах, действующих на расстоянии. В субатомной физике таких сил уже нет: их заменяют взаимодействия между частицами, происходящие через посредство полей, то есть каких-то других частиц. Поэтому физики высоких энергий избегают употреблять слово сила, заменяя его словом взаимодействие^[40].

Взаимодействие каждого типа обусловлено обменом соответствующими «переносчиками»: электромагнитное — виртуальными фотонами, слабое — векторными бозонами, сильное — глюонами (а на больших расстояниях — мезонами). В отношении гравитационного взаимодействия имеются теоретические предположения (например, в теории струн или М-теории), что с ним также может быть связан свой переносчик-бозон, называемый гравитоном, но его существование пока не доказано. Эксперименты по физике высоких энергий, проведённые в 70−80-х годах XX в., подтвердили идею о том, что слабое и электромагнитное взаимодействия являются проявлениями более глобального электрослабого взаимодействия^[41]. В настоящее время делаются попытки объединения всех четырёх фундаментальных взаимодействий в одно (так называемая теория великого объединения).

Всё многообразие проявляющих себя в природе сил в принципе может быть сведено к этим четырём фундаментальным взаимодействиям. Например, трение − это проявление электромагнитных сил, действующих между атомами двух соприкасающихся поверхностей, и принципа запрета Паули^[42], который не позволяет атомам проникать в область друг друга. Сила, возникающая при деформации пружины, описываемая законом Гука, также является результатом действия электромагнитных сил между частицами и принципа запрета Паули, заставляющих атомы кристаллической решётки вещества удерживаться около положения равновесия^[1].

Однако на практике оказывается не только нецелесообразной, но и просто невозможной по условиям задачи подобная детализация рассмотрения вопроса о действии сил.

Гравитация[править | править код]

Гравитация (сила тяготения) — универсальное взаимодействие между любыми видами материи. В рамках классической механики описывается законом всемирного тяготения, сформулированным Ньютоном в уже упомянутом труде «Математические начала натуральной философии». Ньютон получил величину ускорения, с которым Луна движется вокруг Земли, положив при расчёте, что сила тяготения убывает обратно пропорционально квадрату расстояния от тяготеющего тела. Кроме этого, им же было установлено, что ускорение, обусловленное притяжением одного тела другим, пропорционально произведению масс этих тел^[43]. На основании этих двух выводов был сформулирован закон тяготения: любые материальные частицы притягиваются по направлению друг к другу с силой F{\displaystyle F}, прямо пропорциональной произведению масс (m1{\displaystyle m_{1}} и m2{\displaystyle m_{2}}) и обратно пропорциональной квадрату расстояния r{\displaystyle r} между ними:

F=Gm1m2R2.{\displaystyle F=G{\frac {m_{1}m_{2}}{R^{2}}}.}

Здесь G{\displaystyle G} − гравитационная постоянная^[44], значение которой впервые получил в своих опытах Генри Кавендиш. Используя данный закон, можно получить формулы для расчёта силы тяготения тел произвольной формы. Теория тяготения Ньютона хорошо описывает движение планет Солнечной системы и многих других небесных тел. Однако, в её основе лежит концепция дальнодействия, противоречащая теории относительности. Поэтому классическая теория тяготения неприменима для описания движения тел, перемещающихся со скоростью, близкой к скорости света, гравитационных полей чрезвычайно массивных объектов (например, чёрных дыр), а также переменных полей тяготения, создаваемых движущимися телами, на больших расстояниях от них^[45].

Более общей теорией гравитации является общая теория относительности Альберта Эйнштейна. В ней гравитация не характеризуется инвариантной силой, не зависящей от системы отсчёта. Вместо этого свободное движение тел в гравитационном поле, воспринимаемое наблюдателем как движение по искривлённым траекториям в трёхмерном пространстве-времени с переменной скоростью, рассматривается как движение по инерции по геодезической линии в искривлённом четырёхмерном пространстве-времени, в котором время в разных точках течёт по-разному. Причем эта линия в некотором смысле «наиболее прямая» — она такова, что пространственно-временной промежуток (собственное время) между двумя пространственно-временными положениями данного тела максимален. Искривление пространства зависит от массы тел, а также от всех видов энергии, присутствующих в системе^[1].

Электромагнитное взаимодействие[править | править код]

Электростатическое поле (поле неподвижных зарядов)

Развитие физики после Ньютона добавило к трём основным (длина, масса, время) величинам электрический заряд с размерностью «кулон» (C). Однако, исходя из требований практики, в качестве основной единицы измерения стали использовать не единицу заряда, а единицу силы электрического тока. Так, в системе СИ основной единицей является ампер, а единица заряда — кулон — производная от него.

Поскольку заряд как таковой не существует независимо от несущего его тела, электрическое взаимодействие тел проявляется в виде рассматриваемой в механике силы, служащей причиной ускорения. Применительно к электростатическому взаимодействию двух точечных зарядов с величинами q1{\displaystyle q_{1}} и q2{\displaystyle q_{2}}, располагающихся в вакууме, используется закон Кулона. В форме, соответствующей системе СИ, он имеет вид:

F→12=14πε0⋅q1⋅q2r122r→12r12,{\displaystyle {\vec {F}}_{12}={\frac {1}{4\pi \varepsilon _{0}}}\cdot {\frac {q_{1}\cdot q_{2}}{r_{12}^{2}}}{\frac {{\vec {r}}_{12}}{r_{12}}},}

Физика. Понятия и определения.

 

 

 

 

 

 

 

Что такое сила?

Если тело ускоряется то на него что-то действует. А как найти это «что-то»? Например, что за силы действуют на тело вблизи поверхности земли? Это — сила тяжести, направленная вертикально вниз, пропорциональная массе тела и для высот, много меньших, чем радиус земли ${\large R}$, почти независящая от высоты; она равна

${\large F = \dfrac {G  \cdot m \cdot M}{R^2} = m \cdot g }$

где

${\large g = \dfrac {G  \cdot M}{R^2} }$

 

так называемое ускорение силы тяжести. В горизонтальном направлении тело будет двигаться с постоянной скоростью, однако движение в вертикальном направлении по второму закону Ньютона:

 

${\large m \cdot g = m \cdot \left ( \dfrac {d^2 \cdot x}{d \cdot t^2} \right ) }$

 

после сокращения ${\large m}$ получаем, что ускорение в направлении ${\large x}$ постоянно и равно ${\large g}$. Это хорошо известное движение свободно падающего тела, которое описывается уравнениями

${\large v_x = v_0 + g \cdot t}$

${\large x = x_0 + x_0 \cdot t  + \dfrac {1}{2} \cdot g \cdot t^2}$

 

 

В чем сила измеряется?

Во всех учебниках и умных книжках, силу принято выражать в Ньютонах, но кроме как в моделях которыми оперируют физики ньютоны ни где не применяются. Это крайне неудобно.

Ньютон newton (Н) — производная единица измерения силы в Международной системе единиц (СИ).
Исходя из второго закона Ньютона, единица ньютон определяется как сила, изменяющая за одну секунду скорость тела массой один килограмм на 1 метр в секунду в направлении действия силы.

Таким образом, 1 Н = 1 кг·м/с².   

Килограмм-сила (кгс или кГ) — гравитационная метрическая единица силы, равная силе, которая действует на тело массой один килограмм в гравитационном поле земли. Поэтому по определению килограмм-сила равна 9,80665 Н. Килограмм-сила удобна тем, что её величина равна весу тела массой в 1 кг.
1 кгс = 9,80665 ньютонов (примерно ≈ 10 Н)
1 Н ≈ 0,10197162 кгс ≈ 0,1 кгс

1 Н = 1 кг x 1м/с2.

 

 

 

Закон тяготения

Каждый объект Вселенной притягивается к любому другому объекту с силой, пропорциональной их массам и обратно пропорционально квадрату расстояния между ними.

${\large F = G  \cdot \dfrac {m \cdot M}{R^2}}$

 

Добавить можно, что любое тело реагирует на приложенную к нему силу ускорением в направлении этой силы, по величине обратно пропорциональным массе тела.

 ${\large G}$ — гравитационная постоянная

 ${\large M}$ — масса земли

 ${\large R}$ — радиус земли

 

${\large G = 6,67 \cdot {10^{-11}} \left ( \dfrac {m^3}{kg \cdot {sec}^2} \right ) }$

${\large M = 5,97 \cdot {10^{24}} \left ( kg \right ) }$

${\large R = 6,37 \cdot {10^{6}} \left ( m \right ) }$

 

В рамках классической механики, гравитационное взаимодействие описывается законом всемирного тяготения Ньютона, согласно которому сила гравитационного притяжения между двумя телами массы ${\large m_1}$ и ${\large m_2}$, разделённых расстоянием ${\large R}$ есть

${\large F = -G  \cdot \dfrac {m_1 \cdot m_2}{R^2}}$

Здесь ${\large G}$ — гравитационная постоянная, равная ${\large 6,673 \cdot {10^{-11}} m^3 / \left ( kg \cdot {sec}^2 \right ) }$. Знак минус означает, что сила, действующая на пробное тело, всегда направлена по радиус-вектору от пробного тела к источнику гравитационного поля, т.е. гравитационное взаимодействие приводит всегда к притяжению тел.
Поле тяжести потенциально. Это значит, что можно ввести потенциальную энергию гравитационного притяжения пары тел, и эта энергия не изменится после перемещения тел по замкнутому контуру. Потенциальность поля тяжести влечёт за собой закон сохранения суммы кинетической и потенциальной энергии, что при изучении движения тел в поле тяжести часто существенно упрощает решение.
В рамках ньютоновской механики гравитационное взаимодействие является дальнодействующим. Это означает, что как бы массивное тело ни двигалось, в любой точке пространства гравитационный потенциал и сила зависят только от положения тела в данный момент времени.

 

 

Тяжелее — Легче

Вес тела ${\large P}$ выражается произведением его массы ${\large m}$ на ускорение силы тяжести ${\large g}$.

${\large P = m \cdot g}$

 

Когда на земле тело становится легче (слабее давит на весы), это происходит от уменьшения массы. На луне все не так, уменьшение веса вызвано изменением другого множителя — ${\large g}$, так как ускорение силы тяжести на поверхности луны в шесть раз меньше чем на земле.

 

масса земли = ${\large 5,9736 \cdot {10^{24}}\ kg }$

масса луны = ${\large 7,3477 \cdot {10^{22}}\ kg }$ 

 

ускорение свободного падения на Земле = ${\large 9,81\ m / c^2 }$ 

ускорение свободного падения на Луне = ${\large 1,62 \ m / c^2 }$ 

 

В результате произведение ${\large m \cdot g }$, а следовательно и вес уменьшаются в 6 раз.

Но нельзя обозначить оба эти явления одним и тем же выражением «сделать легче». На луне тела становятся не легче, а лишь менее стремительно падают они «менее падучи»))).

 

 

Векторные и скалярные величины

Векторная величина (например сила, приложенная к телу), помимо значения (модуля), характеризуется также направлением. Скалярная же величина (например, длина) характеризуется только значением. Все классические законы механики сформулированы для векторных величин.

 

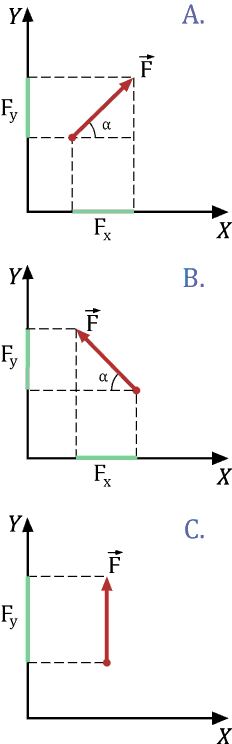
 Рисунок 1.

 

На рис. 1 изображены различные варианты расположения вектора ${ \large \overrightarrow{F}}$ и его проекции ${ \large F_x}$ и ${ \large F_y}$ на оси ${ \large X}$ и ${ \large Y}$ соответственно:

• A.    величины ${ \large F_x}$ и ${ \large F_y}$ являются ненулевыми и положительными
• B.    величины ${ \large F_x}$ и ${ \large F_y}$ являются ненулевыми, при этом ${\large F_y}$ — положительная величина, а ${\large F_x}$ — отрицательная, т.к. вектор ${\large \overrightarrow{F}}$ направлен в сторону, противоположную направлению оси ${\large X}$ 
• C.    ${\large F_y}$ — положительная  ненулевая величина, ${\large F_x}$ равна нулю, т.к. вектор ${\large \overrightarrow{F}}$ направлен перпендикулярно оси ${\large X}$

 

Момент силы

Моментом силы называют векторное произведение радиус-вектора, проведённого от оси вращения к точке приложения силы, на вектор этой силы. Т.е. согласно классическому определению момент силы — величина векторная. В рамках нашей задачи, это определение можно упростить до следующего: моментом силы ${\large \overrightarrow{F}}$, приложенной к точке с координатой ${\large x_F}$, относительно оси, расположенной в точке ${\large x_0}$ называется скалярная величина, равная произведению модуля силы ${\large \overrightarrow{F}}$, на плечо силы — ${\large \left | x_F — x_0 \right |}$. А знак этой скалярной величины зависит от направления силы: если она вращает объект по часовой стрелке, то знак плюс, если против — то минус.

Важно понимать, что ось мы можем выбирать произвольным образом — если тело не вращается, то сумма моментов сил относительно любой оси равна нулю. Второе важное замечание — если сила приложена к точке, через которую проходит ось, то момент этой силы относительно этой оси равен нулю (поскольку плечо силы будет равно нулю). 

 

 

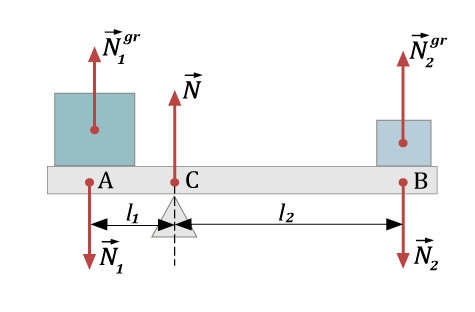
Проиллюстрируем вышесказанное примером, на рис.2. Предположим, что система, изображенная на рис. 2, находится в равновесии. Рассмотрим опору, на которой стоят грузы. На неё действуют 3 силы: ${\large \overrightarrow{N_1},\ \overrightarrow{N_2},\ \overrightarrow{N},}$ точки приложения этих сил А, В и С соответственно. На рисунке также присутствуют силы ${\large \overrightarrow{N_{1}^{gr}},\ \overrightarrow{N_2^{gr}}}$. Эти силы приложены к грузам, и согласно 3-му закону Ньютона

 

${\large \overrightarrow{N_{1}} = — \overrightarrow{N_{1}^{gr}}}$

${\large \overrightarrow{N_{2}} = — \overrightarrow{N_{2}^{gr}}}$

Теперь рассмотрим условие равенства моментов сил, действующих на опору, относительно оси, проходящей через точку А (и, как мы договаривались ранее, перпендикулярную плоскости рисунка):

 

${\large N \cdot l_1 — N_2 \cdot \left ( l_1 +l_2 \right ) = 0}$

Обратите внимание, что в уравнение не вошёл момент силы ${\large \overrightarrow{N_1}}$, поскольку плечо этой силы относительно рассматриваемой оси равно ${\large 0}$. Если же мы по каким-либо причинам хотим выбрать ось, проходящую через точку С, то условие равенства моментов сил будет выглядеть так:

 

${\large N_1 \cdot l_1 — N_2 \cdot l_2  = 0}$

Можно показать, что с математической точки зрения два последних уравнения эквивалентны.

 

 

Центр тяжести

Центром тяжести механической системы называется точка, относительно которой суммарный момент сил тяжести, действующих на систему, равен нулю.

 

 

 

Центр масс

Точка центра масс замечательна тем , что если на частицы образующие тело (неважно будет ли оно твердым или жидким, скоплением звезд или чем то другим) действует великое множество сил (имеются ввиду только внешние силы, поскольку все внутренние силы компенсируют друг друга), то результирующая сила приводит к такому ускорению этой точки, как будто в ней вся масса тела ${\large m}$.

Положение центра масс определяется уравнением:

 

${\large R_{c.m.} = \frac{\sum m_i\, r_i}{\sum m_i}}$

 

Это векторное уравнение, т.е. фактически три уравнения — по одному для каждого из трех направлений. Но рассмотрим только ${\large x}$ направление.  Что означает следующее равенство?

 

${\large X_{c.m.} = \frac{\sum m_i\, x_i}{\sum m_i}}$

 

Предположим тело разделено на маленькие кусочки с одинаковой массой ${\large m}$, причем полная масса тела равна будет равна числу таких кусочков ${\large N}$, умноженному на массу одного кусочка, например 1 грамм. Тогда это уравнение означает, что нужно взять координаты ${\large x}$ всех кусочков, сложить их и результат разделить на число кусочков. Иными словами, если массы кусочков равны то ${\large X_{c.m.}}$ будет просто средним арифметическим ${\large x}$ координат всех кусочков.

 

 

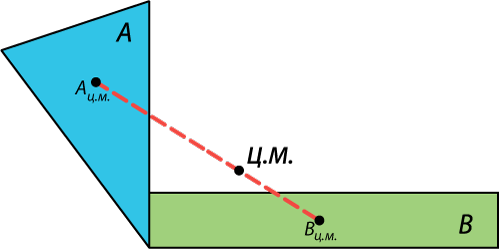центр масс сложного тела лежит на линии, соединяющей центры масс двух составляющих его частей

 

 

 

Масса и плотность

Масса — фундаментальная физическая величина. Масса характеризует сразу несколько свойств тела и сама по себе обладает рядом важных свойств.

 

• Масса служит мерой содержащегося в теле вещества.
• Масса является мерой инертности тела. Инертностью называется свойство тела сохранять свою скорость неизменной (в инерциальной системе отсчёта), когда внешние воздействия отсутствуют или компенсируют друг друга. При наличии внешних воздействий инертность тела проявляется в том, что его скорость меняется не мгновенно, а постепенно, и тем медленнее, чем больше инертность (т.е. масса) тела. Например, если бильярдный шар и автобус движутся с одинаковой скоростью и тормозятся одинаковым усилием, то для остановки шара требуется гораздо меньше времени, чем для остановки автобуса.
• Массы тел являются причиной их гравитационного притяжения друг к другу (см. раздел «Сила тяготения»).
• Масса тела равна сумме масс его частей. Это так называемая аддитивность массы. Аддитивность позволяет использовать для измерения массы эталон — 1 кг.
• Масса изолированной системы тел не меняется со временем (закон сохранения массы).
• Масса тела не зависит от скорости его движения. Масса не меняется при переходе от одной системы отсчёта к другой.
• Плотностью однородного тела называется отношение массы тела к его объёму:

 ${\large p = \dfrac {m}{V} }$

 

Плотность не зависит от геометрических свойств тела (формы, объёма) и является характеристикой вещества тела. Плотности различных веществ представлены в справочных таблицах. Желательно помнить плотность воды: 1000 кг/м3.

 

 

Второй и третий законы Ньютона

Взаимодействие тел можно описывать с помощью понятия силы. Сила — это векторная величина, являющаяся мерой воздействия одного тела на другое.
Будучи вектором, сила характеризуется модулем (абсолютной величиной) и направлением в пространстве. Кроме того, важна точка приложения силы: одна и та же по модулю и направлению сила, приложенная в разных точках тела, может оказывать различное воздействие. Так, если взяться за обод велосипедного колеса и потянуть по касательной к ободу, то колесо начнёт вращаться. Если же тянуть вдоль радиуса, никакого вращения не будет.

Второй закон Ньютона

Произведение массы тела на вектор ускорения есть равнодействующая всех сил, приложенных к телу:

${\large m \cdot \overrightarrow{a} = \overrightarrow{F} }$

Второй закон Ньютона связывает векторы ускорения и силы. Это означает, что справедливы следующие утверждения.

1. ${\large m \cdot a = F}$, где ${\large a}$ — модуль ускорения, ${\large F}$ — модуль равнодействующей силы.
2. Вектор ускорения имеет одинаковое направление с вектором равнодействующей силы, так как масса тела положительна.

Третий закон Ньютона

Два тела действуют друг на друга с силами, равными по модулю и противоположными по направлению. Эти силы имеют одну и ту же физическую природу и направлены вдоль прямой, соединяющей их точки приложения.

 

 

 

Принцип суперпозиции

Опыт показывает, что если на данное тело действуют несколько других тел, то соответствующие силы складываются как векторы. Более точно, справедлив принцип суперпозиции.
Принцип суперпозиции сил. Пусть на тело действуют силы ${\large \overrightarrow{F_1}, \overrightarrow{F_2},\ \ldots \overrightarrow{F_n}}$  Если заменить их одной силой ${\large \overrightarrow{F} =  \overrightarrow{F_1} + \overrightarrow{F_2} \ldots + \overrightarrow{F_n}}$, то результат воздействия не изменится.
Сила ${\large \overrightarrow{F}}$ называется равнодействующей сил ${\large \overrightarrow{F_1}, \overrightarrow{F_2},\ \ldots \overrightarrow{F_n}}$ или результирующей силой.
 

 

 

Единицы силы. Измерение силы. Динамометр

План-конспект урока по теме «Единица силы. Измерение силы. Динамометр»

Дата:

Тема: «Единица силы. Измерение силы. Динамометр»

Цели:

Образовательная: усвоение определения основной единицы силы(1 ньютон), формирование понятия «динамометр»;

Развивающая: понимание устройства и принципа действия динамометра; развивать познавательный интерес;

Воспитательная: прививать культуру умственного труда, аккуратность, учить видеть практическую пользу знаний, продолжить формирование коммуникативных умений, воспитывать внимательность, наблюдательность.

Тип урока: урок усвоения новых знаний

Оборудование и источники информации:

Исаченкова, Л. А. Физика : учеб. для 7 кл. учреждений общ. сред. образования с рус. яз. обучения / Л. А. Исаченкова, Г. В. Пальчик, А. А. Сокольский ; под ред. А. А. Сокольского. Минск : Народная асвета, 2017.

Структура урока:

1. Организационный момент (5 мин)

2. Актуализация опорных знаний (5мин)

3. Изучение нового материала (15 мин)

4. Физкультминутка (1 мин)

5. Закрепление знаний (14 мин)

6. Итоги урока (5 мин)

Содержание урока

1. Организационный момент (проверка присутствующих в классе, проверка выполнения домашнего задания , озвучивание темы и основных целей урока )

2. Актуализация опорных знаний

Сила характеризуется числовым значением(модулем), направлением и точкой приложения. Чтобы определить числовое значение силы, нужно измерить силу, т. е. сравнить ее с другой силой, принятой в качестве единицы силы. Что принято за единицу силы?

3. Изучение нового материала

Главный результат действия силы — изменение скорости движения тела, которая сама по себе никогда не изменяется. Исходя из этого, была выбрана в СИ единица силы — 1 ньютон (1 Н), названная в честь английского ученого Исаака Ньютона. Существуют кратные и дольные единицы силы: 1 кН = 1000 Н, 1 мН = 0,001 Н.

Сила, как вы знаете, может не только изменить скорость, но и вызвать деформацию тела. Пружина растягивается (рис. 143), потому что на нее действует вес груза, который притягивает Земля.

Какой массой должно обладать тело, чтобы действующая на него сила тяжести равнялась 1,0 Н? Исследования показали, что с силой F = 1,0 Н

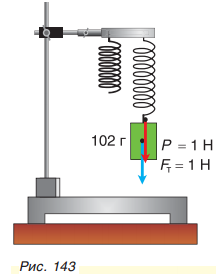
Земля притягивает тело массой т = 0,102 кг. Определим значение коэффициента g, входящего в формулу силы тяжести F= gm. Из формулы видно, что g = . Так как на тело массой 0,102 кг.

Земля действует с силой F = 1,0 Н, то:

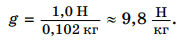
Значит, если масса тела равна 1,0 кг, то действующая на него сила тяжести F = gm = 9,8 Н. Следовательно, и вес этого тела (если оно находится в состоянии покоя или движется равномерно) Р = 9,8 Н. Ни в коем случае нельзя приравнивать вес и массу, что, к сожалению, часто встречается в быту. Это разные физические величины, и единицы у них разные. Масса измеряется в килограммах, вес — в ньютонах (рис. 144).

Если ваша масса m = 50 кг, то ваш вес Р = 500 Н.

Как измерить силу? Для этого нужно создать измерительный прибор. Будем подвешивать к пружине сначала одну гирю массой т = 102 г = 0,102 кг, затем две, три и т. д. Отметим метками положения указателя (рис. 145), напротив которых ставим значения 1 Н, 2 Н, 3 Н и т. д.

Пружина с указателем и шкалой представляет собой прибор для измерения сил — динамометр (от греч. dynamis — сила и metreo — измеряю) (рис. 146). Динамометром можно измерять не только вес тела, но и любые силы.

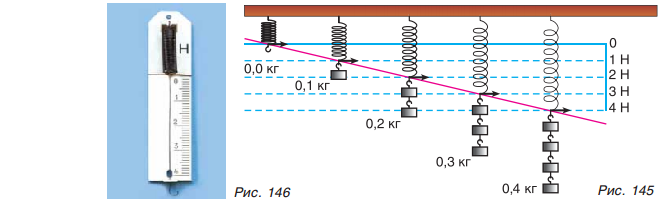
Динамометры бывают различных типов и размеров в зависимости от того, для измерения больших или малых сил они предназначены. Для измерения мускульной силы руки используют динамометр-силомер (рис. 147, а). Определить силу тяги трактора позволяет тяговый динамометр (рис. 147, б).

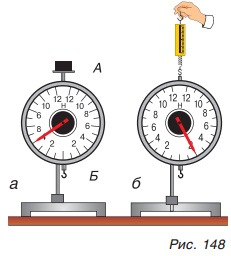
Для проведения различных исследований удобен динамометр с реечной передачей (рис. 148). Он позволяет измерять не только силу, направленную вниз, например создаваемую лежащим на опоре А телом (рис. 148, а), или вес подвешенного к подвесу Б тела. Таким динамометром можно измерить и силу, направленную вверх (рис. 148, б).

4. Физкультминутка

5. Закрепление знаний

Рассмотрим пример решение задачи из учебника на странице 90:

Ответьте устно на вопросы:

• В каких единицах в СИ измеряется сила?

• Какие свойства силы используются для ее измерения?

• Какой массой должно обладать тело, чтобы Земля притягивала его с силой F =1 Н?

• С какой силой вас притягивает Земля?

• Можно ли измерить вес тела с помощью пружинного динамометра, находясь на орбите в космическом корабле?

6. Итоги урока

Итак, подведем итоги:

• В СИ единицей силы является1 ньютон.

• Силу измеряют с помощью динамометра.

• С силой F =1 Н Земля притягивает тело массой m =0,102 кг.

• В формуле Fт = gm силы тяжести, с которой Земля действует на тело, постоянный коэффициент g≈9,8 Н/кг.

Организация домашнего задания

§25,ответить на контрольные вопросы, упр.9 №2,3.

Рефлексия

Продолжите фразы:

• Сегодня на уроке я узнал…

• Было интересно…

• Знания, которые я получил на уроке, пригодятся…

Как измеряют силу, чем она характеризуется | Природоведение. Реферат, доклад, сообщение, краткое содержание, лекция, шпаргалка, конспект, ГДЗ, тест

Раздел:

Физические величины и механизмы

Силу можно измерить. Ее измеряют при помощи прибора, имеющего название динамометр (на греческом языке слово «динамис» значит «сила», а «метро» — «измеряю»). На рисунке 84 изображены динамометры, которые используются в школе и в быту. Несмотря на отличия во внешнем виде, все они имеют пружину, стрелку и шкалу.

Единицей измерения силы является ньютон (Н). Так ее назва­ли в честь известного английского ученого Исаака Ньютона. Как вы считаете, большая или маленькая сила, значение которой равно 1Н? Известно, что для поднятия тела массой 1 кг необхо­димо применить силу приблизительно равную 10 Н. Таким обра­зом, зная массу школьного портфеля, наполненного учебниками, каждый из вас сможет легко определить значение силы, с кото­рой этот портфель приходится каждый раз поднимать.

Кроме числового значения, сила характеризуется еще и направ­лением. Па рисунках направление действия силы указывают стрелкой. Например, на рисунке 85 указаны направления силы персонажей басни «Лебедь, Рак и Щука». Материал с сайта http://worldofschool.ru

Рис. 84. Динамометры: 1 — школьный лабораторный; 2 — школьный демонстрационный; 3 — бытовой

Рис. 85. Направления действия силы персонажей басни «Лебедь, Рак и Щука»

На этой странице материал по темам:

• Сыла характерезуеться

• Что такое сила и чем она характеризуется?

• Что такое сила и чем она характеризуется

Вопросы по этому материалу:

• Назовите единицы измерения и прибор для измерения силы.

Ньютон (единица измерения) — Википедия

Материал из Википедии — свободной энциклопедии

У этого термина существуют и другие значения, см. Ньютон.

Нью́то́н (русское обозначение: Н; международное: N) — единица измерения силы в Международной системе единиц (СИ).

Ньютон — производная единица. Исходя из второго закона Ньютона она определяется как сила, изменяющая за 1 секунду скорость тела массой 1 кг на 1 м/с в направлении действия силы. Таким образом, 1 Н = 1 кг·м/с².

В соответствии с общими правилами СИ, касающимися производных единиц, названных по имени учёных, наименование единицы ньютон пишется со строчной буквы, а её обозначение — с заглавной. Такое написание обозначения сохраняется и в обозначениях других производных единиц, образованных с использованием ньютона. Например, обозначение единицы момента силы ньютон-метр записывается как Н·м.

Определение единицы силы, как силы, придающей телу с массой 1 килограмм ускорение в 1 метр в секунду за секунду, было принято для системы единиц МКС Международным комитетом мер и весов (МКМВ) в 1946 году. В 1948 году IX Генеральная конференция по мерам и весам (ГКМВ) ратифицировала данное решение МКМВ и утвердила для этой единицы наименование «ньютон». В Международной системе единиц (СИ) ньютон стал использоваться с момента её принятия XI ГКМВ в 1960 году^[1][2].

Единица названа в честь английского физика Исаака Ньютона, открывшего законы движения и связавшего понятия силы, массы и ускорения. В своих работах, однако, Исаак Ньютон не вводил единиц измерения силы и рассматривал её как абстрактное явление.^[3] Измерять силу в ньютонах стали спустя более чем два века после смерти великого учёного, когда была принята система СИ.

С другими единицами измерения силы ньютон связывают следующие выражения:

Десятичные кратные и дольные единицы образуют с помощью стандартных приставок СИ.

Кратные				Дольные
величина	название	обозначение		величина	название	обозначение
101 Н	деканьютон	даН	daN	10−1 Н	дециньютон	дН	dN
102 Н	гектоньютон	гН	hN	10−2 Н	сантиньютон	сН	cN
103 Н	килоньютон	кН	kN	10−3 Н	миллиньютон	мН	mN
106 Н	меганьютон	МН	MN	10−6 Н	микроньютон	мкН	µN
109 Н	гиганьютон	ГН	GN	10−9 Н	наноньютон	нН	nN
1012 Н	тераньютон	ТН	TN	10−12 Н	пиконьютон	пН	pN
1015 Н	петаньютон	ПН	PN	10−15 Н	фемтоньютон	фН	fN
1018 Н	эксаньютон	ЭН	EN	10−18 Н	аттоньютон	аН	aN
1021 Н	зеттаньютон	ЗН	ZN	10−21 Н	зептоньютон	зН	zN
1024 Н	иоттаньютон	ИН	YN	10−24 Н	иоктоньютон	иН	yN
применять не рекомендуется

Динамометр — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 4 июля 2019; проверки требует 1 правка. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 4 июля 2019; проверки требует 1 правка. Динамометр общего назначения на 400 кН

Динамо́ме́тр (от др.-греч. δύναμις — «сила» и μέτρεω — «измеряю») — прибор для измерения силы или момента силы, состоит из силового звена (упругого элемента) и отсчётного устройства. В силовом звене измеряемое усилие вызывает деформацию, которая непосредственно или через передачу сообщается отсчётному устройству. Существующими динамометрами можно измерять усилия от долей ньютонов (н, долей кгс) до 20 Мн (2000 тс). По принципу действия различают динамометры механические (пружинные или рычажные), гидравлические и электронные. Иногда в одном динамометре используют два принципа.

Пружинные весы Приборная доска самолёта Ан-140, самая верхняя пара приборов — ИКМ двигателей, 4 % — крутящий момент на минимальном режиме («Тихое руление»)

Первыми приборами для измерения силы стали весы, первое изображение которых было напечатано в 1726 году. Около 1830 года Сальтер предложил более удобное устройство: для измерения силы в нём использовалась пружина, которая растягивалась грузом. Ещё раньше Ренье изобрёл динамометр с циферблатом, в котором использовалась кольцеобразно-замкнутая пружина. Более поздними изобретениями являются нажим Прони и динамометры Томсона, Геффнер-Альтенека, Броуна и Межи^[1].

Существует несколько типов динамометров: механические динамометры (рычажные и пружинные), а также гидравлические и электрические.

Механический динамометр[править | править код]

Существует два вида механических динамометров: пружинный и рычажный. В пружинном динамометре сила или момент силы передаётся пружине, которая в зависимости от направления силы сжимается или растягивается. Величина упругой деформации пружины пропорциональна силе воздействия и регистрируется. В рычажном динамометре действие силы деформирует рычаг, величина деформации которого после регистрируется.

Гидравлический динамометр[править | править код]

Действие гидравлического динамометра основано на вымещении измеряемой силой жидкости из цилиндра. Под давлением жидкость поступает по трубке к записывающему аппарату или датчику и регистрируется. Гидравлический динамометр используется как измеритель крутящего момента (ИКМ) двигателя турбовинтового самолёта, его данные используются для оценки работы двигателя, а также для автоматического флюгирования винта при отказе двигателя. ИКМ может быть выполнен в виде нескольких цилиндров, удерживающих корпус планетарного редуктора винта от проворота — давление, требуемое для удержания, является функцией крутящего момента, такой ИКМ входит в состав редуктора двигателя АИ-20 и многих других. В редукторе же двигателя НК-12 бомбардировщика Ту-95 и транспортного самолёта Ан-22, приводящем соосные винты, разместить такой ИКМ негде, поэтому там ИКМ выполнен как щель в одном из валов, за счёт скручивания вала изменяется расход масла через щель, что и является исходной величиной для ИКМ.

Электрический динамометр[править | править код]

Электрический динамометр состоит из датчика, который преобразует деформацию от воздействия силы в электрический сигнал, и дополнительного датчика, который усиливает и записывает электрический сигнал первого датчика. Для преобразования силы или момента силы в деформацию используются индуктивные, пьезоэлектрические, тензорезисторные и вибрационно-частотные датчики сопротивления. Под действием силы датчик деформируется и токи моста сопротивления изменяются. Сила электрического сигнала прямо пропорциональна деформации элемента и в итоге силе воздействия. Второй датчик усиливает сигнал и записывает его для последующей обработки.

Примеры повседневного использования[править | править код]

В повседневной жизни прибор используется для измерения силы сжатия створок автоматически закрывающихся систем, таких как двери автобусов, трамваев, вагонов поездов, метро, а также двери пассажирских и грузовых лифтов, гаражные ворота, автомобильные окна, сдвигающиеся люки на крыше и так далее. Так как все эти системы могут в случае неправильной юстировки стать причиной травм, разработаны и внедрены технические нормы, определяющие предельные значения сил сжатия в закрывающихся системах. Данные нормы^[2] обязательны во всех странах Европейского союза, а также используются в США, Японии, Китае, Саудовской Аравии, Австралии и других странах мира.